
Многостадийные задачи принятия решений 1
Постановка задачи 1
Дерево решений 1
Детерминистский случай. Метод Беллмана 3
Многостадийные задачи принятия решений в условиях неопределенности 5
Расчет одноуровневого дерева решений 5
Расчет двухуровневого дерева решений 6
Марковские модели принятия решений 11
Многостадийные задачи принятия решений Постановка задачи Дерево решений
Примеры, которые мы рассматривали до сих пор, включали в себя единственное решение. Однако на практике результат одного решения заставляет нас принимать следующее и т.д. Эту последовательность нельзя выразить матрицей решений, поэтому нужно использовать какой-то другой способ описания и решения задачи.
Понятие многостадийной (многоэтапной, многошаговой) задачи принятия решений весьма многогранно. Поэтому могут рассматриваться совершенно различные модели многостадийности от простых до достаточно сложных. Мы здесь остановимся на обсуждении некоторых традиционных подходов к проблеме, позволяющих уяснить главные черты и особенности многостадийных задач принятия решений в условиях неопределенности. В частности, будем предполагать, что решаемая проблема является одноцелевой. Например, весьма часто цель всей операции заключается в максимизации "доходов" (прибыли, полезности) или минимизации "затрат". Предполагается, что получение "доходов" реализуется на каждом этапе процесса принятия решений, а затем эти "доходы" суммируются (принцип аддитивности).
Рассматриваемая далее модель многостадийной задачи принятия решений предполагает наличие некоторого графа, называемого деревом решений и, по существу, описывающего то, как можно попадать из заданного множества его начальных вершин в заданное множество его конечных вершин.
Схема дерево решений очень похожа на граф связей альтернатив с исходами. Ее используют, когда нужно принять несколько решений, когда каждое решение зависит от исхода предыдущего или множества исходов. Дерево решений, отображает структуру проблемы. Располагаются деревья слева направо.

На схеме используются два типа узлов: квадратные узлы обозначают точки, где принимается решение, круглые узлы – множество альтернатив и множество исходов.
Ветви показывают, какие из альтернативных решения могут быть приняты в решающей вершине, и возможные исходы, возникающие в результате этих решений. На схеме используется два вида ветвей: первый – пунктирные линии, соединяющие квадраты с узлами возможных решений, второй – сплошные линии, соединяющие кружки возможных альтернатив и множества исходов.
На рис. 4.1 дан пример так называемого детерминистского дерева решений, описывающего процесс принятия решений в условиях определенности.
В этом случае граф содержит только
«решающие» вершины. С каждой из решающих
вершин ассоциируется некоторое состояние
![]() в котором находится объект принятия
решений. Наличие нескольких дуг, входящих
в вершину, показывает, что в нее можно
попасть различными способами. Дуги
выходящие из вершины соответствуют
возможным переходам из данного состояния
в другое в зависимости от принимаемых
решений. Все расходы, вызванные
решением, проставляются на соответствующей
ветви: каждая ветвь графа имеет свой
вес – вещественное число, означающее
соответствующие локальные «затраты»
на переход в другое состояние.
в котором находится объект принятия
решений. Наличие нескольких дуг, входящих
в вершину, показывает, что в нее можно
попасть различными способами. Дуги
выходящие из вершины соответствуют
возможным переходам из данного состояния
в другое в зависимости от принимаемых
решений. Все расходы, вызванные
решением, проставляются на соответствующей
ветви: каждая ветвь графа имеет свой
вес – вещественное число, означающее
соответствующие локальные «затраты»
на переход в другое состояние.
Предполагается, что процесс разворачивается во времени, чему соответствует движение по графу слева направо. Допустимые начальные и конечные вершины заштрихованы.
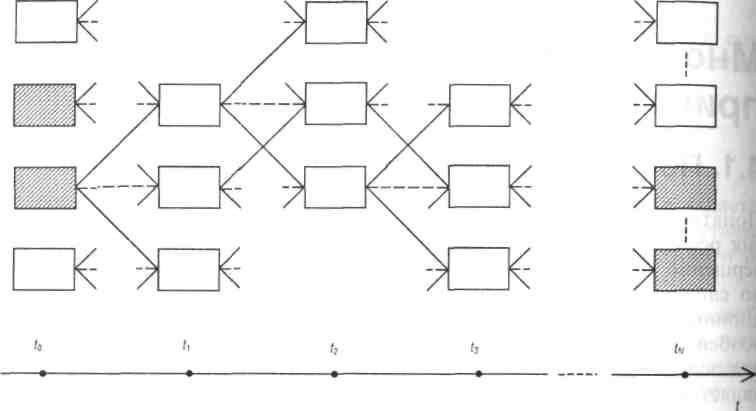
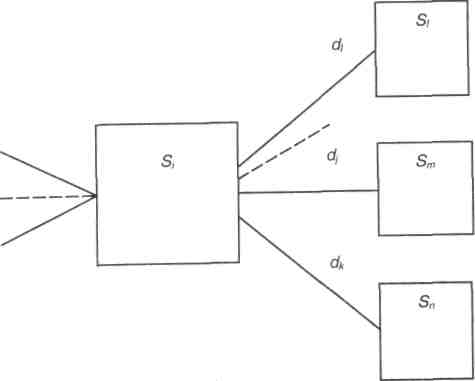
Рис. 4.1. Дерево решений в условиях определенности
Задача состоит в оптимальном выборе начальной вершины (из множества допустимых) и пути из нее в любую из допустимых конечных вершин. Оптимальность понимается в смысле построения допустимого пути реализующего минимальные суммарные затраты (задача выбора минимального пути на графе). В частном случае множества допустимых начальных и конечных вершин могут быть одноэлементными.
Более сложная ситуация возникает в ситуации принятия решений в условиях риска, когда выбор конкретного решения определяет не новое состояние системы, а задает некоторую лотерею на множестве возможных новых состояний (плотность распределения вероятности) (рис. 4.3).
Фактически в конечномерном случае
(который и рассматривается) это означает,
что выбор альтернативы приведет к одному
из возможных исходов в соответствии с
заданными вероятностями
![]() (рис. 4.3), где
(рис. 4.3), где
![]() .
.
В случае полной неопределенности структура дерева сохраняется, но ветви, исходящие из вершин соответствующих множеству альтернатив, уже не будут иметь весов (распределение вероятности не известно).

Заметим, что вершины промежуточных исходов в приведенных примерах совпадают с решающими вершинами, поэтому с каждой из них связывается определенный доход (оценка исхода) заданный условиями задачи или полученный в результате расчетов.
