Относительные равновесия гибкой нити привязанной к спутнику на круговой орбите
Рассмотрим вращающуюся систему
координат
.
Ее угловая скорость постоянна и направлена
по оси
.
В точке
помещена материальная точка, порождающая
гравитационное поле с гравитационной
постоянной
,
а на оси
на расстоянии
находится массивный спутник, к которому
привязана однородная гибкая нерастяжимая
нить длины
.
Угловая скорость вращения системы
координат соответствует угловой скорости
вращения спутника на круговой орбите
и равна
.
Предполагается, что движение нити не
возмущает движения спутника. Требуется
найти положения равновесия нити
относительно вращающейся системы
координат и исследовать их устойчивость.
Представим радиус вектор точки нити
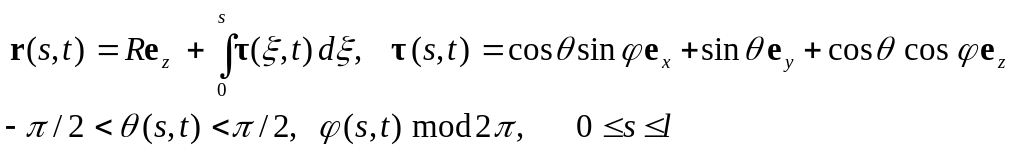(22)
где
- орты соответствующих осей. Заметим,
что ось
ортогональна плоскости орбиты, а ось
параллельна касательной к орбите
движения спутника. Поскольку система
координат
не инерциальная, то уравнения движения
нити с учетом центробежных и кориолисовых
сил инерции представляются в виде
(23)
Последние два условия в (22) являются
кинематическими граничными условиями
– условие закрепления нити на спутнике
и динамическим граничным условием –
равенство нулю натяжения нити на ее
свободном конце. Здесь
- натяжение и линейная плотность нити
соответственно. Поля центробежных и
гравитационных сил, действующие на
точки гибкой нити, потенциальны, и их
потенциал равен
(24)
Первая вариация функционала (24)
обращается в нуль на кривых, определяющих
положения равновесии нити, при условии
.
Это условие запишем так
(25)
Вариация (25) обращается в нуль, если
выполняются условия
.
Этим условиям соответствуют конфигурации
нити, расположенные вдоль круговой
орбиты спутника. При этом нить может
быть «сложена» вдоль орбиты, имея
конечное или счетное число перегибов.
В точках орбиты гравитационное поле
уравновешивается полем центробежных
сил, и натяжение нити равно нулю.
Другая совокупность положений равновесия соответствует нити, сложенной вдоль оси , поскольку суммарное силовое поле, действующее на точки нити, направлено вдоль этой оси. Этим положениям равновесия соответствуют значения углов сферической системы координат
(26)
где
- борелевское множество, полученное
путем разбиения интервала
на конечное или счетное число интервалов
и дальнейшего отбрасывания любой их
совокупности. Среди этих положений
равновесия существуют две конфигурации
нити, вытянутой вдоль оси
в положительном и отрицательном
направлениях, при которых натяжение
нити положительно на всей ее длине. Этим
конфигурациям соответствуют значения
угла
и угла
.
Покажем, что на этих конфигурациях
вариация потенциала (25) обращается в
ноль. Для конфигурации
получим
Аналогично для конфигурации
найдем
Исследуем устойчивость найденных
конфигураций. Прежде всего, заметим,
что рассматриваемая механическая
система имеет первый интеграл – интеграл
Якоби или обобщенный интеграл энергии.
Умножим уравнение движения (23) на
и проинтегрируем полученное равенство
по
от нуля до
.
Заметим, что
так как
.
В результате получим
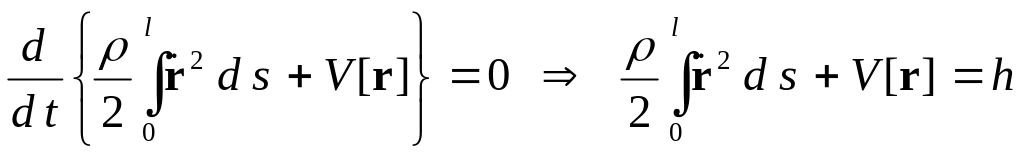(27)
Устойчивость исследуемых положений равновесия следует из положительной определенности обобщенного интеграла энергии (27) в окрестности положений равновесия. Функционал
в этом случае является функционалом
Ляпунова, и согласно теореме Ляпунова
положения равновесия устойчивы. Покажем,
что потенциал
имеет изолированный минимум на
рассматриваемых положениях равновесия.
Для этого достаточно показать, что
вторая вариация потенциала гравитационных
и центробежных сил положительна. Найдем
вторую вариацию
(28)
Отметим, что вектор
выражается через независимые лагранжевы
переменные
и
.
Согласно равенству (22) получим
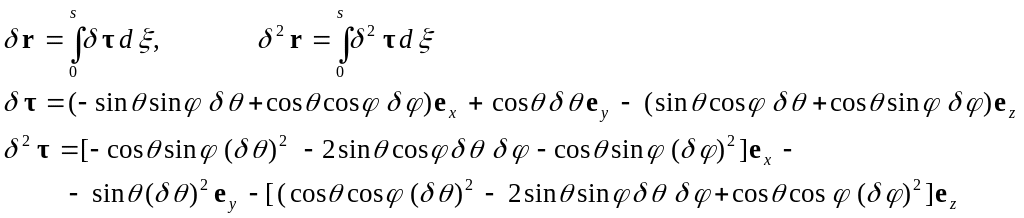
На конфигурациях нити (26) найденные вариации принимают значения
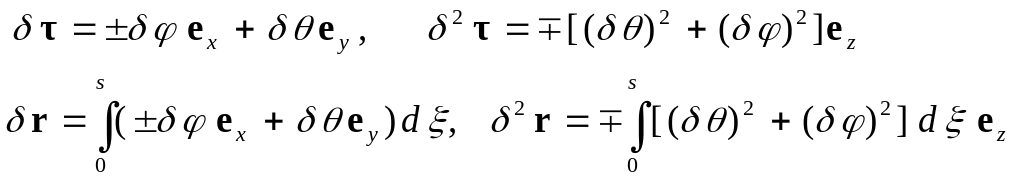
Верхний знак соответствует конфигурации
,
а нижний -
.
Вторая вариация (28) принимает вид
(29)
Здесь
.
Выпишем выражение, содержащее вариацию
под знаком интеграла в (29)
и
получим оценку
(30)
Выражение, содержащее вариацию
под знаком интеграла в соотношении
(29), имеет вид
(31)
Используем неравенство Коши-Буняковского
и получим из равенства (31) неравенство
В результате приходим к оценке
(32)
Неравенства (30) и (32) свидетельствуют о том, что вторая вариация функционала потенциальных сил положительна, и функционал имеет изолированный минимум на конфигурациях, соответствующих положениям равновесия нити вытянутой вдоль оси по направлениям от и к притягивающему центру. Заметим, что в рассматриваемом случае отклонения нити от положения равновесия и ее скорости следует измерять в нормах соответствующих функциональных пространств.