
2.Расчет структуры переменных электромагнитных полей в волноводе.
Общее задание
Для заданного типа волны с начальной амплитудой поля E0 = 5кВ/см, распространяющейся в прямоугольном волноводе сечением ab, получить аналитические выражения продольной и поперечных компонент полей в комплексной форме записи и для мгновенных значений. Для численных параметров задачи построить эпюры полей по осям x, y, z, а также картину распределения полей в плоскостях xy и xz. Рассчитать заданные характеристики полей и построить их зависимости от частоты.
Параметры задачи
Волна E43, ab = 3515 мм; l = 8 мм; диэлектрическая проницаемость e = 3. Рассчитать ф и гр.
Решение
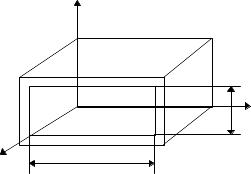
Оси координат расположим в соответствии с рис. 2.1.
 y
y
x b
z a
Рисунок 2.1.
Полость волновода заполнена диэлектриком, электрическая проницаемость которого e. Длина волновода в направлении оси z не ограничена. Процесс распространения электромагнитных волн в полости прямоугольного волновода рассматриваем, полагая, что стенки волновода выполнены из сверхпроводящего материала (g = ¥). При этом условии напряженность электрического поля на стенках волновода будет равна нулю (плотность тока на стенках волновода d = gE есть величина конечная, поэтому при g®¥, E®0).[2]
Электромагнитное поле в волноводе описывается волновым уравнением:
![]() (2.1)
(2.1)
где – круговая частота, а и а – абсолютные электрическая и магнитная проницаемости.
Для заданного типа волны выполняется следующее условие:
Ez 0, Hz = 0, m = 4, n = 3.
Распространяющиеся в волноводе электромагнитные волны являются волнами, бегущими вдоль оси волновода (оси z) и стоячими в двух остальных направлениях.
Тот факт, что волны являются бегущими вдоль оси z, в формально математи-ческом отношении находит свое выражение в том, что каждая из составляющих волн, при записи ее имеет множитель exp(*t-kp*z), где kp – коэффициент распространения.
Если подставить в уравнение (2.1), то последнее разобьется на три уравнения для проекций. Для проекции на ось z будем иметь следующее уравнение:
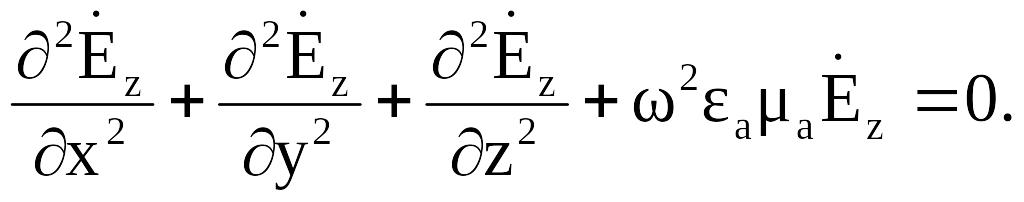 (2.2)
(2.2)
Упростим уравнение (2.3) путем подстановки решения вида:
![]() ,
(2.3)
,
(2.3)
справедливого для гармонических процессов в волноводах [2], где
![]() – продольный
коэффициент распространения в волноводе,
– длина волны в волноводе. Множитель
– продольный
коэффициент распространения в волноводе,
– длина волны в волноводе. Множитель
![]() выражает
собой то обстоятельство, что вдоль оси
z движется бегущая волна.
выражает
собой то обстоятельство, что вдоль оси
z движется бегущая волна.
Подставляем (2.3) в (2.2):
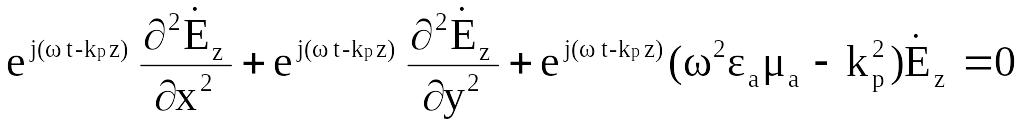
Заменим
![]() и поделим
на
.
Получим:
и поделим
на
.
Получим:
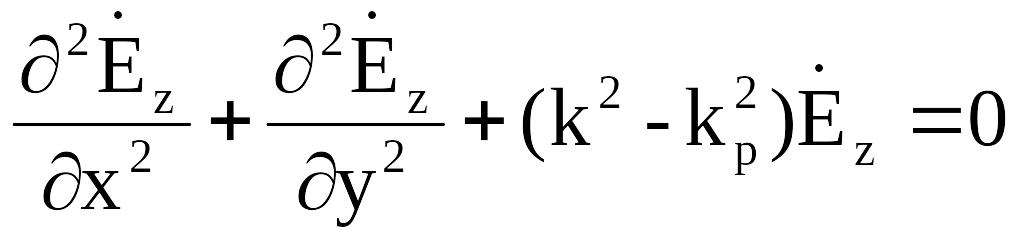 (2.4)
(2.4)
Воспользуемся методом разделения переменных и искомую функцию представим в виде:
![]() (2.5)
(2.5)
и подставим в
(2.4), получаем:
![]()
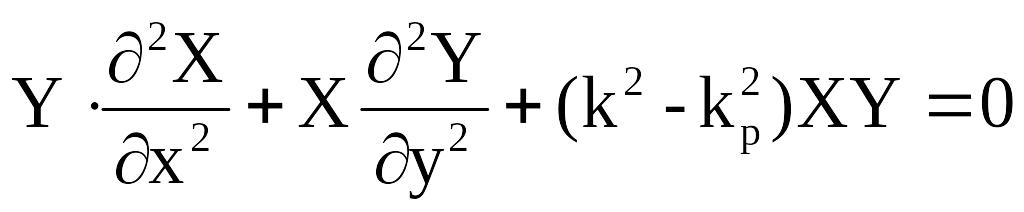
Разделим это уравнение на XY, получим:
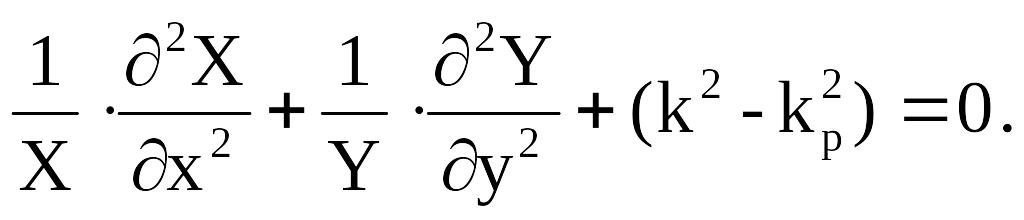 (2.6)
(2.6)
Сумма двух функций
 и
и
![]() ,
из которых одна является функцией только
x, а другая – функцией только y, может
равняться постоянному числу только в
том случае, если каждая из этих функций
есть постоянное число. Перейдем от
частных производных к обыкновенным и
положим:
,
из которых одна является функцией только
x, а другая – функцией только y, может
равняться постоянному числу только в
том случае, если каждая из этих функций
есть постоянное число. Перейдем от
частных производных к обыкновенным и
положим:
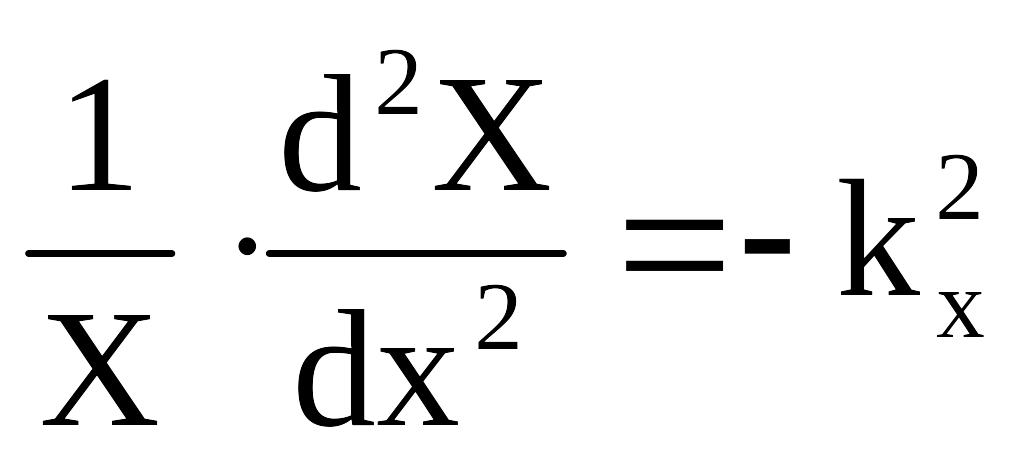
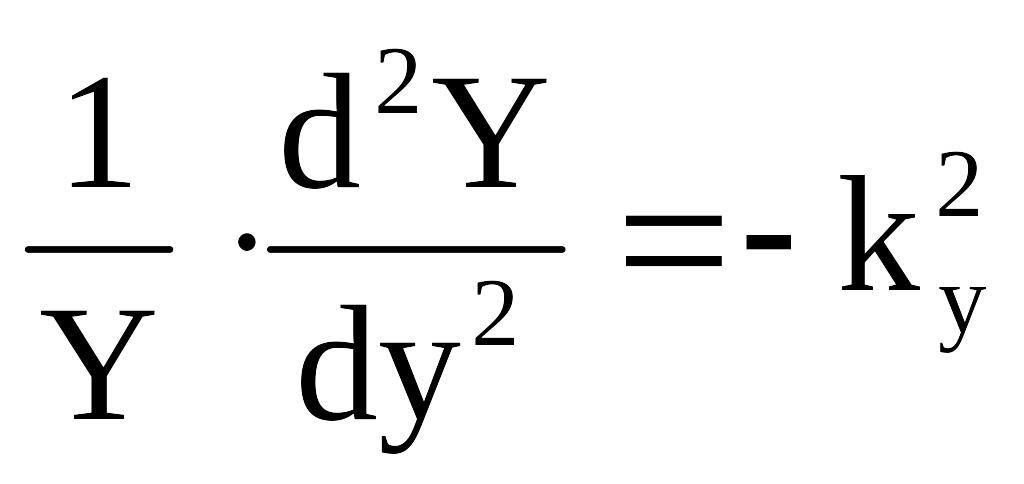
Здесь через kx и ky обозначены постоянные разделения (поперечные волновые числа), удовлетворяющие равенствам:
X(x)=Cxsin(kxx+φx), Y(y)= Cxsin(kxx+φx).
Исходя из соотношения (2.5), имеем выражение для амплитуды (волновой множитель опускаем) продольной составляющей электрического поля:
![]() (2.7)
(2.7)
где
![]() – начальная
комплексная амплитуда; kx,
ky,
x
и y
–
постоянные
интегрирования.
– начальная
комплексная амплитуда; kx,
ky,
x
и y
–
постоянные
интегрирования.
Для нахождения поперечных компонент поля воспользуемся уравнениями Максвелла в проекциях на оси координат[1,2]:
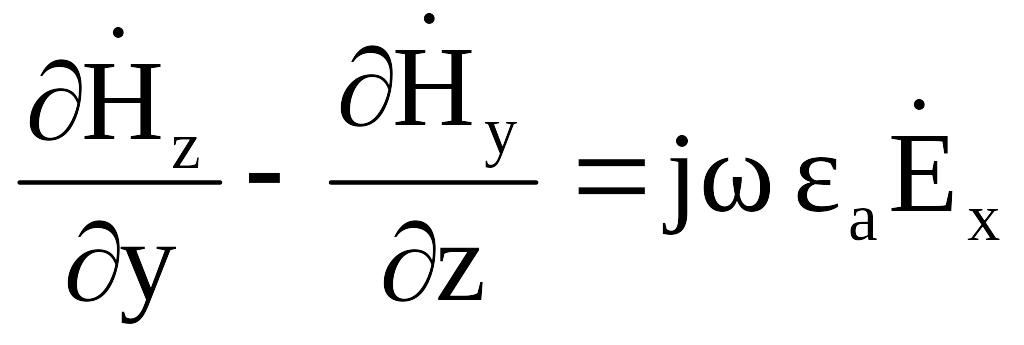 (2.8)
(2.8) 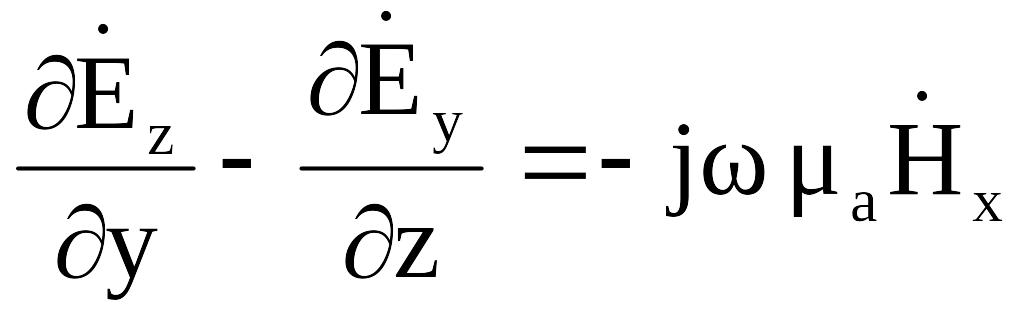 (2.11)
(2.11)
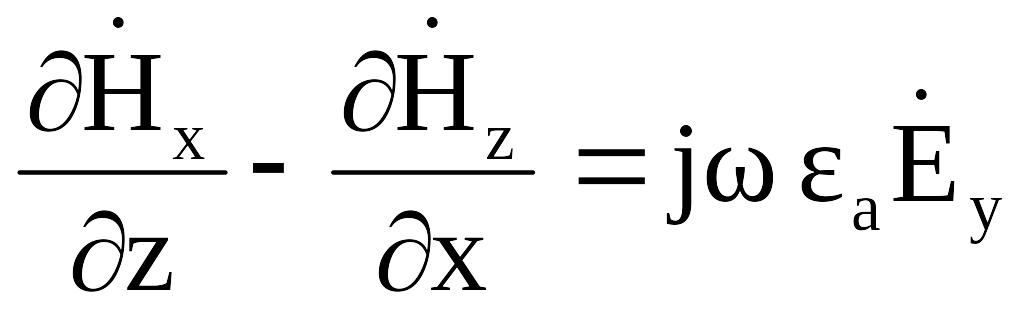 (2.9)
(2.9) 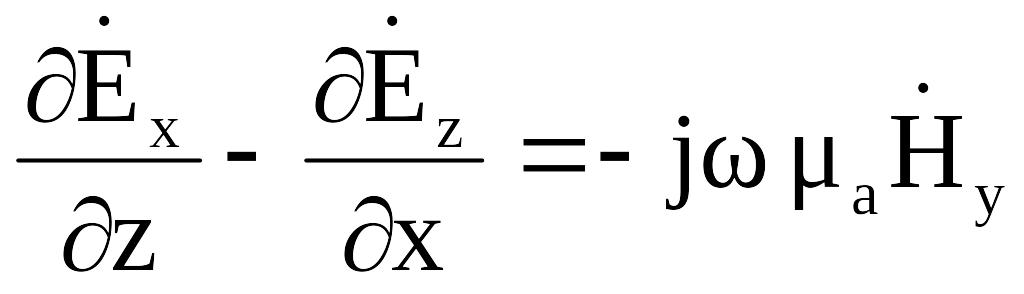 (2.12)
(2.12)
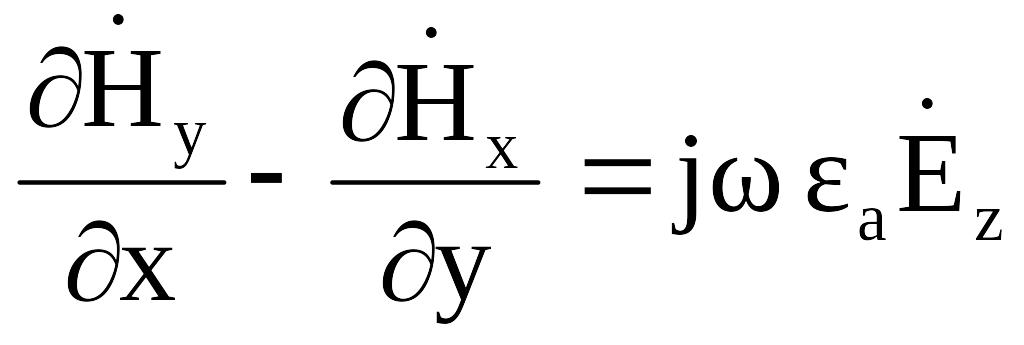 (2.10)
(2.10)
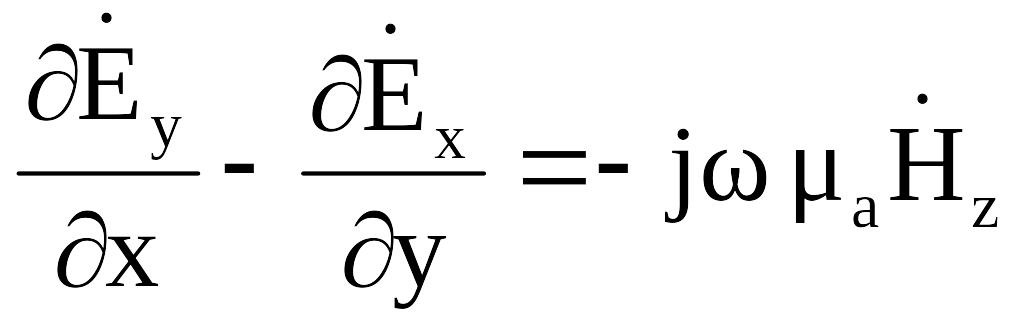 (2.13)
(2.13)
В силу того, что
для E-волны
![]() ,
то уравнения (2.8), (2.9), (2.13) можно упростить,
убрав выражения, содержащие
,
то уравнения (2.8), (2.9), (2.13) можно упростить,
убрав выражения, содержащие
![]() :
:
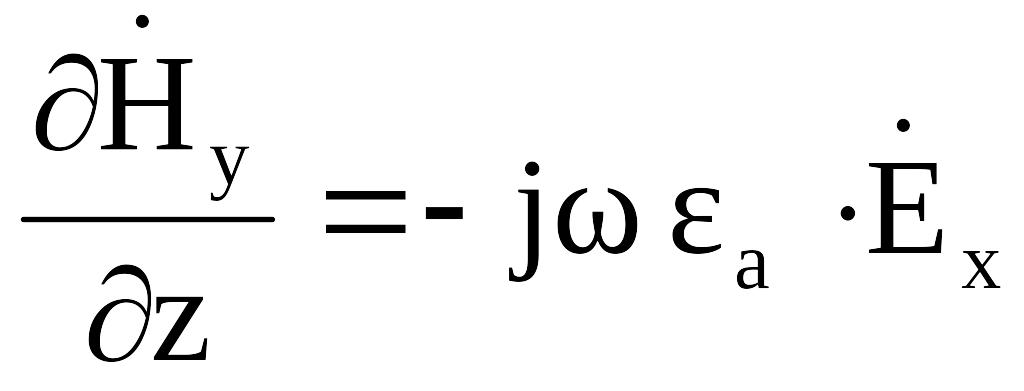
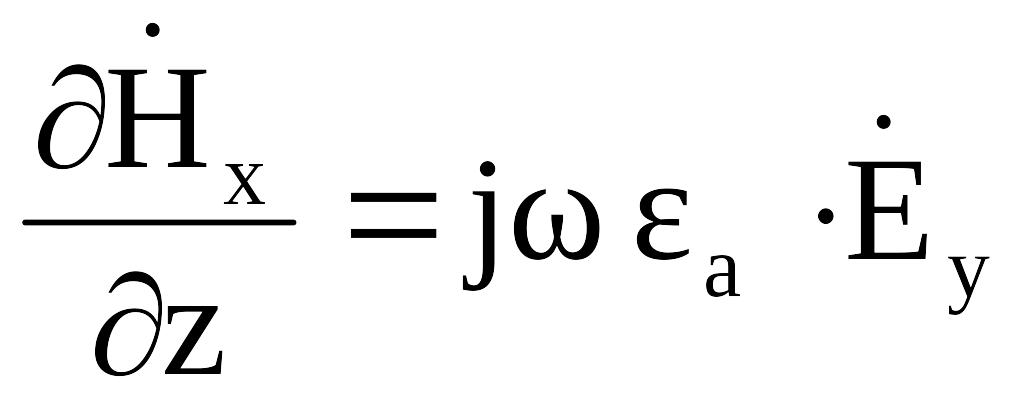
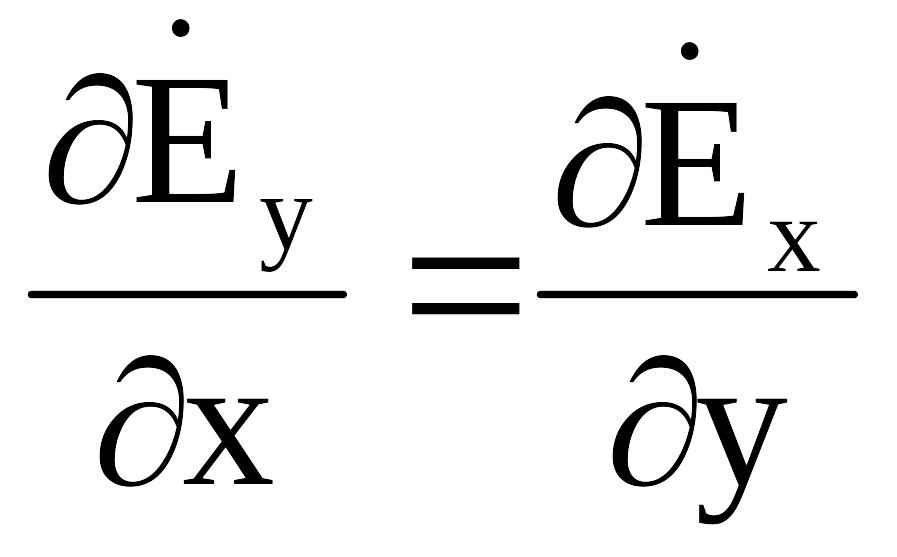
Поскольку характер изменения полей по оси z задается выражением (2.4), то в (2.8)-(2.13) примем, что:
![]() .
.
Рассмотрим
теперь уравнения (2.8) и (2.12) как систему
для
![]() и
и
![]() ,
а уравнения
(2.9) и (2.11) —
,
а уравнения
(2.9) и (2.11) —
![]() и
и
![]() :
:
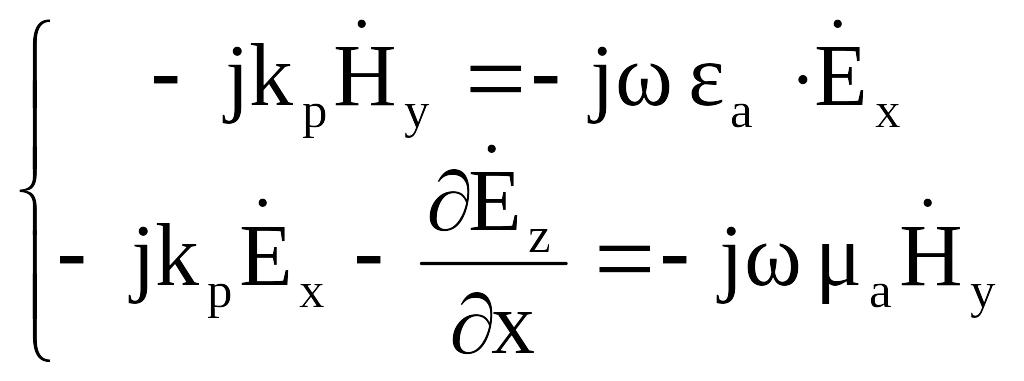
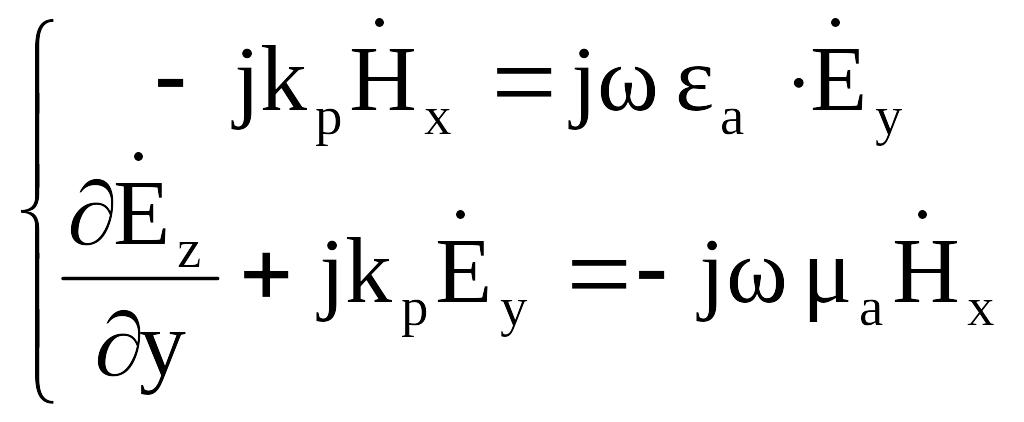

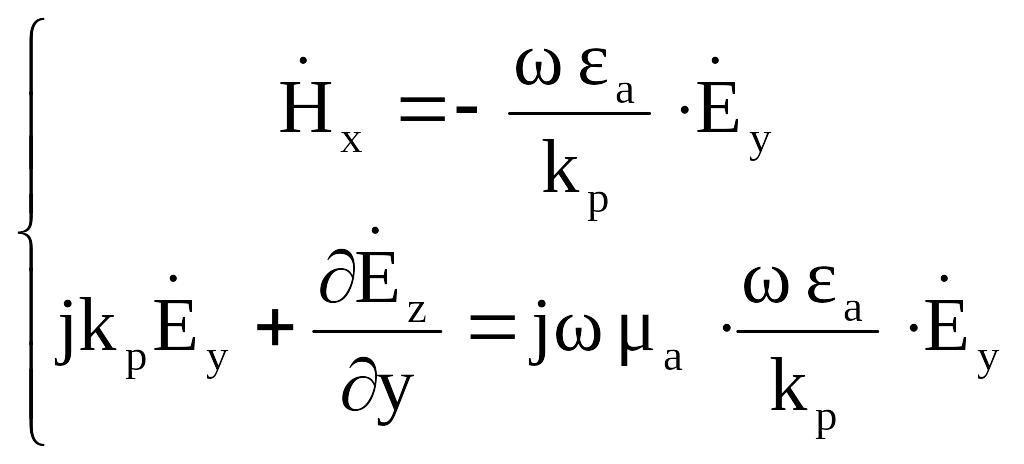
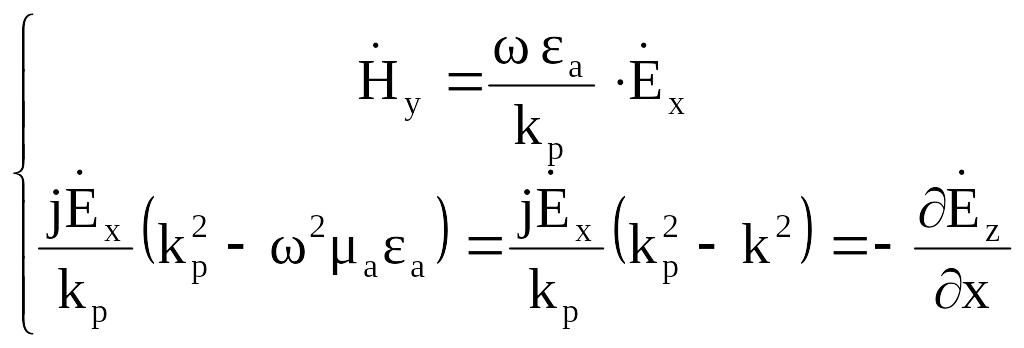
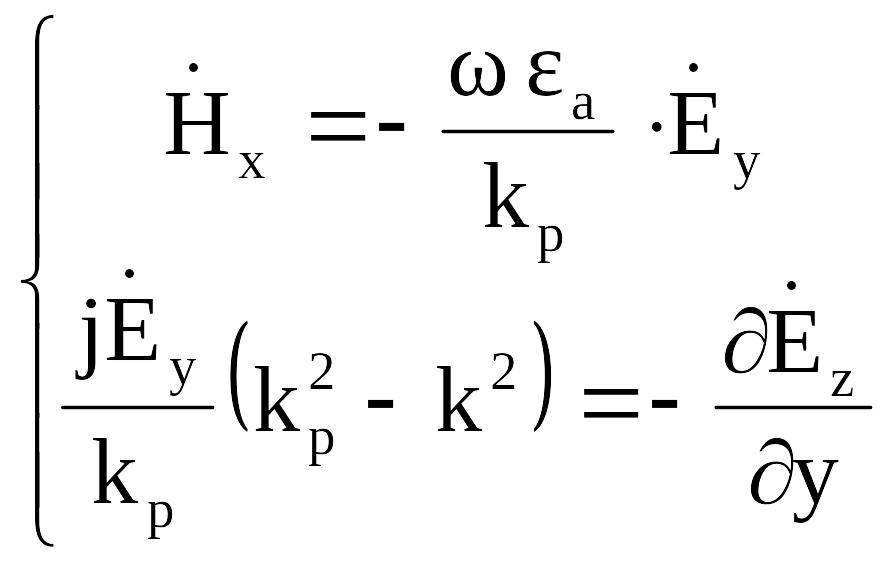

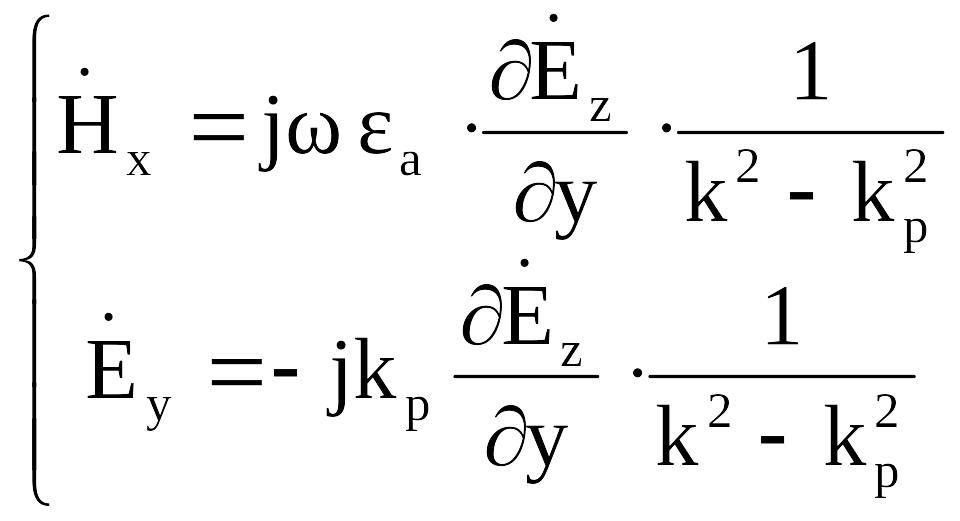 (2.14)
(2.14)
Подставляя в
(2.14) значение
![]() ,
получаем выражения для поперечных
составляющих поля:
,
получаем выражения для поперечных
составляющих поля:
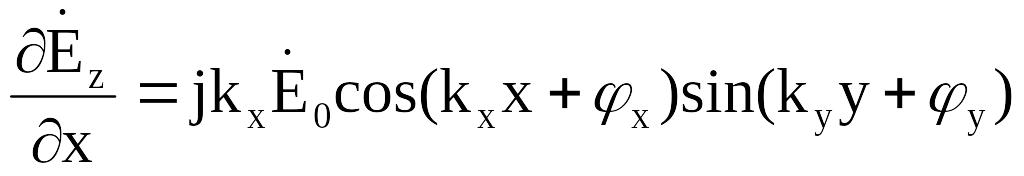
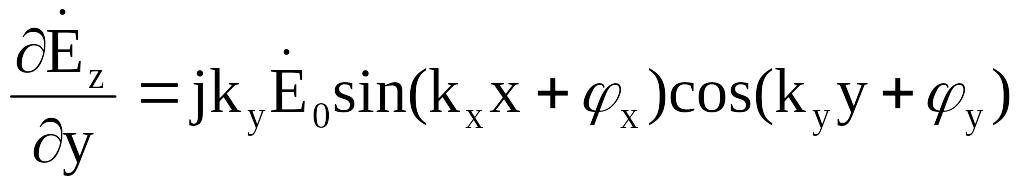

 (2.15)
(2.15)
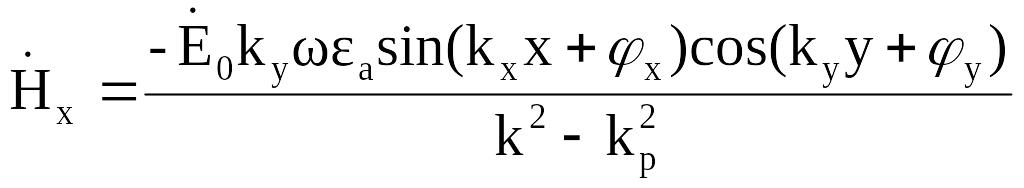
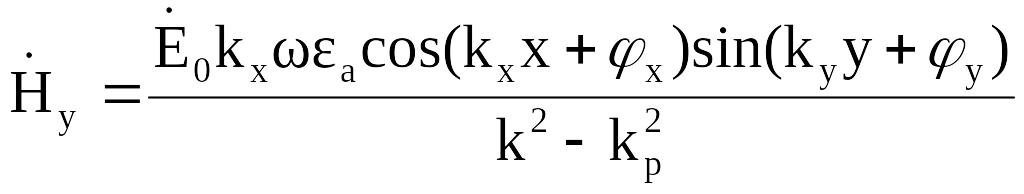
В соответствии с
граничными условиями на стенках волновода
![]() =
0 при x=0 и x=a,
а
=
0 при x=0 и x=a,
а
![]() =
0 при y=0 и
y=b. Тогда:
=
0 при y=0 и
y=b. Тогда:

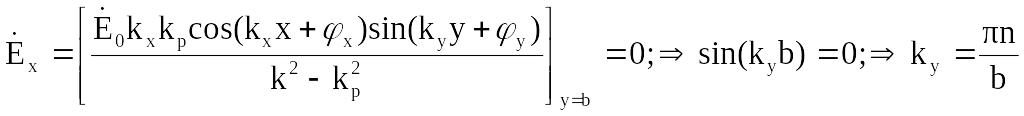 ,
где
n
= 0, 1, 2, …
,
где
n
= 0, 1, 2, …
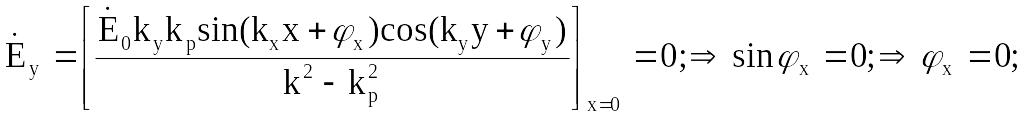
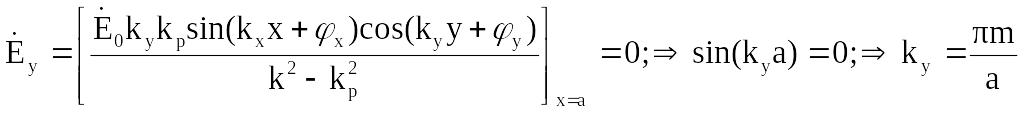 ,
где m
= 0, 1, 2, …
,
где m
= 0, 1, 2, …
Окончательное
выражение для составляющих поля после
подстановки найденных постоянных, а
также после подстановки
![]() ,
примет вид:
,
примет вид:

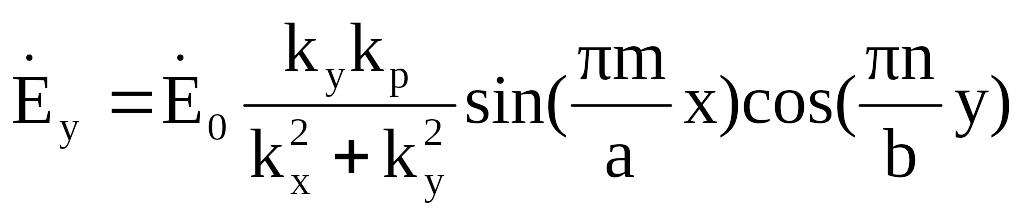

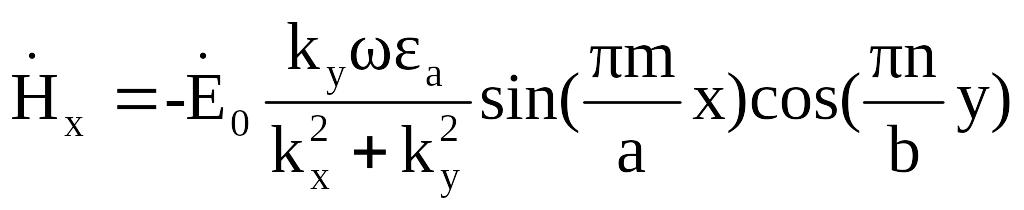
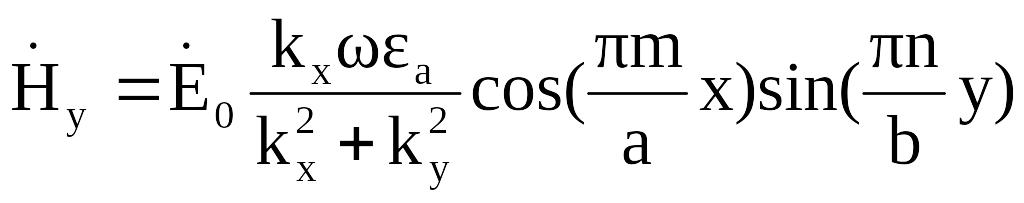
Заменим a:
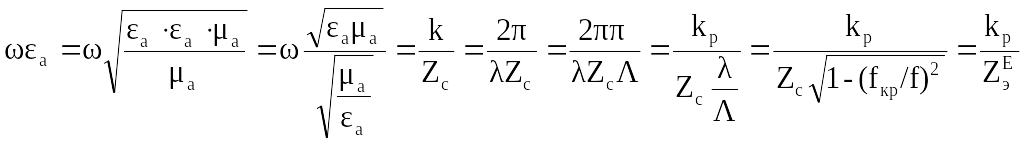 ,
где
,
где
![]() —
эквивалентное сопротивление волновода
для Е-волны [3];
—
эквивалентное сопротивление волновода
для Е-волны [3];
![]() — волновое сопротивление неограниченной
среды; fкр
—
критическая частота.
— волновое сопротивление неограниченной
среды; fкр
—
критическая частота.
Тогда:
(2.16)
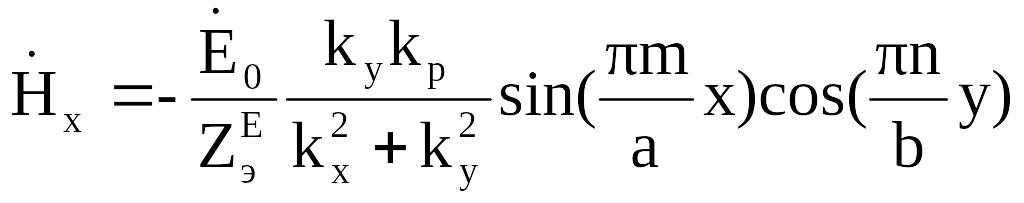
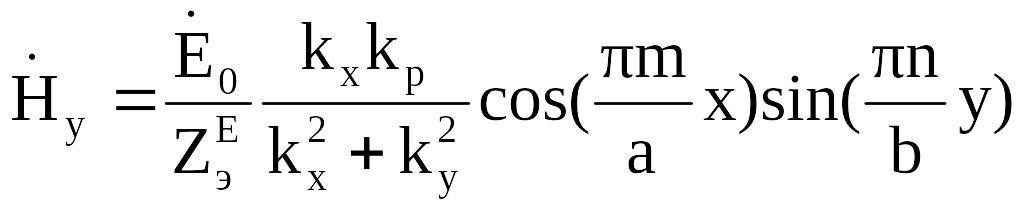
Аналитические выражения для составляющих поля волны Е43 получаем из (2.16) при m = 4 и n = 3:


 (2.16)
(2.16)


Для восстановления действительных значений необходимо компоненты полей домножить на опущенный ранее волновой множитель , перейти по формуле Эйлера [4] к тригонометрической форме записи и взять действительную часть полученного выражения:
![]()

![]()

![]()

![]()

![]()

Получили:


 (2.17)
(2.17)


Длина волны в волноводе и эквивалентное сопротивление волновода для Е-волны в общем случае определяются следующими соотношениями [1, 2]:
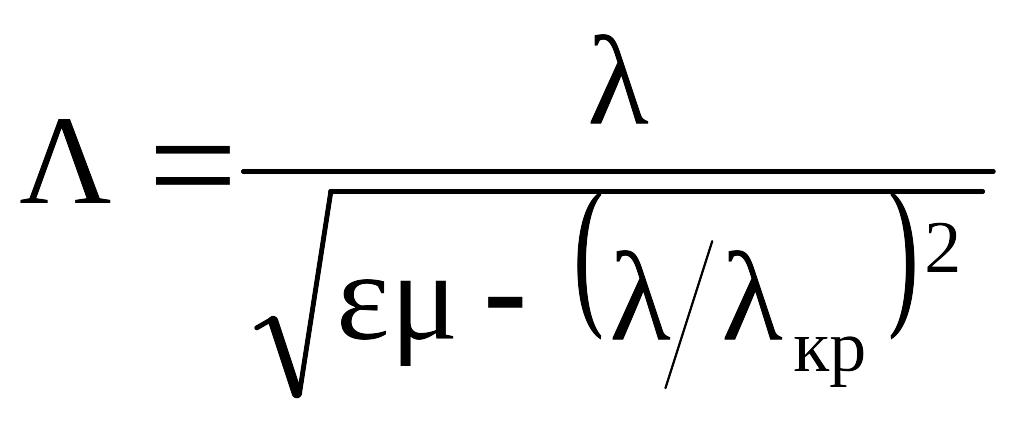 ,
, ![]() ,
,
где — волновое сопротивление неограниченной среды; кр — критическая длина волны, которая равна:

Подставив значения, получаем:

Фазовая и групповая скорости в общем случае определяются следующими соотношениями:
ф =
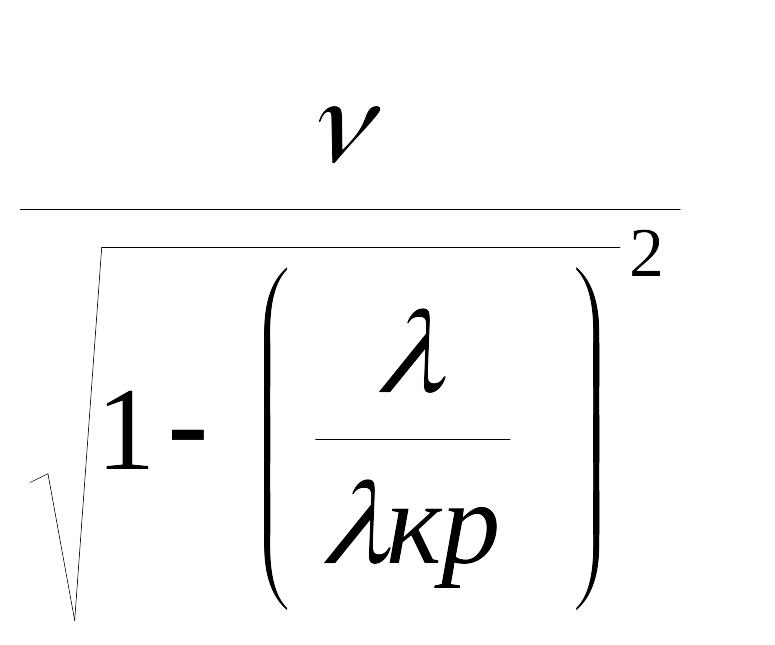 гр
=
гр
= 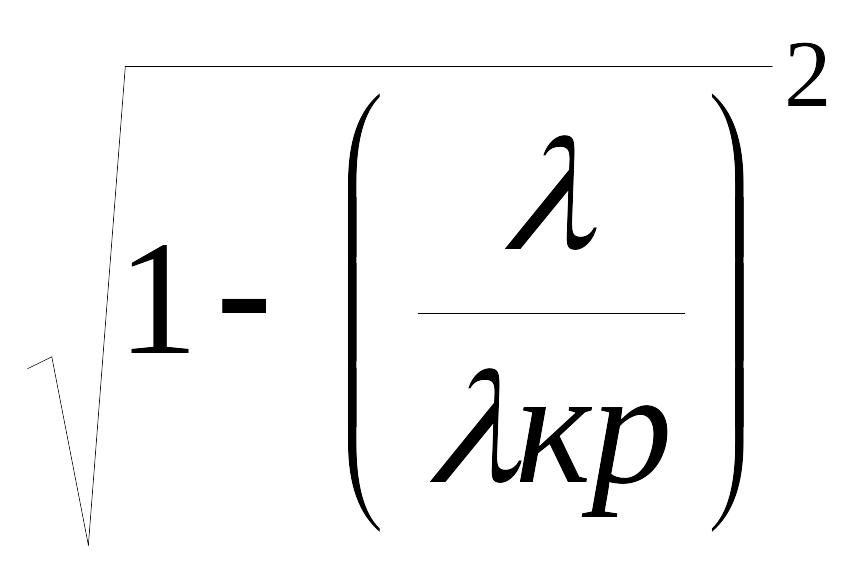 (2.18)
(2.18)
Где
![]()
-скорости електромагнитной волны в неограниченной среде с параметрами εа и µа, состветствующими параметрами диелектрического заполнения волновда:
=![]()
ф=
 (м/с)
(м/с)
гр =
 (м/с)
(м/с)
Для соотношений (2.17), (2.18) составляем блок-схему и программу расчета зависимостей компонент поля от координат волновода и значений ф и гр от .
Вывод
При выполнении курсовой работы были приобретены навыки по расчету структуры стационарных потенциальных полей и переменных электромагнитных полей в направляющих системах, а также закреплены навыки основ программирования и работы на персональном компьютере.
В соответствии с заданием на курсовую работу были выведены выражения для потенциала и напряженности полей, рассчитаны (с помощью ЭВМ) семейство эквипотенциальных линий для цилиндрической полости в диэлектрической среде.
В случае переменного электромагнитного поля в прямоугольном волноводе получены аналитические выражения для электрических и магнитных компонент поля, построены их распределения в поперечном и продольном сечениях. В поперечных сечениях волновода вдоль осей x и у образуются стоячие волны в результате наложения многократных отражений от стенок волновода электромагнитного поля. Длина волны в волноводе больше длины волны в свободном пространстве. При таком условии возможно нормальное распространение электромагнитных волн (без затухания).
