4.4. Определение реакций в однопролетных статически неопределимых стержневых элементах

Сначала определим выражения изгибающих моментов и попе­речных сил в однопролетных балках при единичных угловых пере­мещениях или при единичных относительных линейных смещени­ях концевых сечений (рис. 4, а).

Дифференциальное уравнение изгиба балок с постоянным по­перечным сечением при отсутствии внешних нагрузок, действу­ющих в пролете, записывается в виде:

Рис.4

. (2.19)

Общее решение одно­родного дифференциально­го уравнения (2.16) запи­шем в следующем виде:

, (2.20)

откуда

. (2.21)

Вводим следующие гра­ничные условия:

при х = 0, у = у₀ ;  = ₀ ;

при х = l, y = y_l ;

 = _l . (2.22)

C учетом граничных условий задачи (2.22) из (2.20) и (2.21), получим:

c₄ = у₀ ;    c₃ = ₀ ; c₁ l₃ + c₂ l₂ + ₀ l + у₀ = y_l ;

3 c₁ l₂ + 2 c₂ l + ₀ = _l . (2.23)

В результате совместного рассмотрения уравнений (2.23) полу­чим выражения произвольных постоянных с_i (i = 1,2,3,4), представ­ленное в следующем виде:

Далее определим выражения M и Q:

(2.24)

Для примера вычислим значения M и Q в концевых сечениях для балки с двумя защемленными концами при ₀ = 1. В данном случае имеем: _l = y_l = у₀ = 0.

Подставляя эти значения в (2.24) получим:

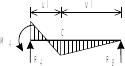
Результаты расчетов эпюры моментов и поперечных сил для однопролетных статически неопределимых балок с различными граничными условиями их закрепления и при различном характере кинематического нагружения обобщены в таблице1 .Ординаты эпюры моментов отложены со стороны рас­тянутого волокна.

Для определения эпюры моментов в однопролетных статически неопределимых балочных элементах основной системы от действия внешних сил, удобно применить метод сил.

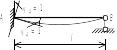
Так например, однопролетная балка, изображенная на рис. 4, б, трижды статически неопределима. А балка, изображен­ная на рис. 4, в, один раз статически неопределима. Для удоб­ства, результаты расчетов эпюры моментов однопролетных стати­чески неопределимых элементах, с различными граничными усло­виями их закрепления, от действия наиболее часто встречающихся силовых и температурных нагружений, обобщены в таблице 1.

При неравномерном нагреве по высоте поперечного сечения балки и при равномерном нагреве по ее длине, изгибающие мо­менты и поперечные силы определяются согласно общеизвестных выражений:

,

где   температурный коэффициент линейного расширения; h высота поперечного сечения; х  независимая переменная 0  x  l; l  длина элемента.

В заключении заметим, что применяя метод перемещений, сле­дует твердо придерживается какоголибо определенного правила знаков. Принять, что углы поворота опорного сечения, а также реактивный момент, действующий на балку со стороны заделки, положительны, если в результате оси поворачиваются по часовой стрелке. Линейное смещение узла принято положительным, если оно совпадает по направлению с положительной реакцией, вызыва­ющей растяжение опорного сечения стержня.

\Таблица 1

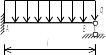
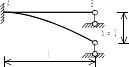
№ n/n	Схема балки и воздействия на нее	Эпюры изгибающих моментов1) и реакции	Формулы
1.
2.
3.
4.
5.			2)
6.
7.
8.
9.
10.			2)

Примечание. 1) ординаты отложены со стороны растянутого волокна.; 2) h  высота поперечного сечения;   температурный коэффициент линейного расширения.