Глава 1. Материал и методика

Материалом для исследования антропологической вариации народов Кавказского реги-она послужили обстоятельные данные, собранные по единой методике и опубликованные четырьмя авторами: Г.Ф.Дебецем (1956), М.Г.Абдушелишвили (1964), А.Г.Гаджиевым (1971), Р.М.Касимовой, (1975). Выбор именно этих материалов диктуется двумя обстоятельствами. Во-первых, они практически исчерпывающе описывают все этнически группы региона. Во-вторых, для них возможно внесение более или менее надежных поправок на субъективность индивидуальных приемов оценок многих антропоскопических показателей, используемых разными авторами. Эта серия данных включала (Приложение 1) 221 выборку.

Для рассмотрения антропологического статуса народов Кавказа на широком расовом фоне дополнительно для анализа были привлечены данные по населению Афганистана (Дебец, 1965, 1966, 1966а, 1967, 1968, 1968а, 1980), Памира (Рычков, 1969), Индии (Чебоксаров, 1980; Абдушелишвили, 1980, 1982), Южного Йемена (Гохман и др.,1995; Чистов, 1998), Восточной Европы (Дебец, 1933, 1941, 1941а; Зенкевич, 1941; Чебоксаров, 1946; Трофимова 1949; Алексеева, 1955; Денисова, 1956, 1958; Витов и др., 1959; Марк, 1960, 1975; Витов, 1964, 1997; Происхождение и этническая история русского народа, 1965; Дяченко, 1965; Акимова, 1974; Алексееу и др., 1994), Финляндии (Марк, 1975), Центральной Европы (Чебоксаров, 1941; Тот, 1974), Греции (Пулянос, 1961), Албании (Dhima, 1994). И здесь выбор материалов диктовался, главным образом, возможностями получения методически сопоставимых данных. Так, существующие весьма представительные материалы по населению Передней Азии, собранные Г.Филдом (Field, 1939, 1940, 1949), неполностью сопоставимы по многим методическим приемам с остальными сериями выборок и для этого региона возможно привлечение данных только по небольшому количеству измерительных показателей. Мы использовали новейшую сводку материалов по антропологии этого региона, составленную Ю.К.Чистовым (1998). Аналогичным образом, для населения Центральной Европы нами были использованы материалы из сводки Н.Н.Чебоксарова (1941). Здесь доступным для сравнительного изучения был относительно небольшой набор признаков. Для морфологической высоты лица Н.Н.Чебоксаровым в необходимых случаях были внесены правдоподобные поправки. Из описательной программы нами привлекались только данные по цветности глаз и волос как опирающиеся на хорошо разработанные и сопоставимые шкалы, что, вероятно, не требует использования методов коннексии. Из сводки А.Дхимы по албанцам (Dhima, 1994) мы использовали только данные К.Куна и самого А.Дхимы, так как для многих других материалов, как нам

- 4 -

показалось, не была полностью гарантирована унифицированность методики измерения высоты лица. В результате в рассмотрение были включены 895 выборок (Приложение 1).

* * *

В ситуации, когда материалы по расовому составу современного населения собираются разными авторами, возникает проблема методической сопоставимости антропоскопических оценок многих балловых признаков. В значительной степени эти трудности могут быть устранены применением коннексии методических приемов разных авторов к некоторому единому стандарту (Дебец, 1947; Алексеева, 1965, 1973). В частности, существует возможность коннексии методических приемов Г.Ф.Дебеца, Н.Н.Чебоксарова, Т.В.Трофи-мовой, П.И.Зенкевича Р.Я.Денисовой к стандарту Русской антропологической экспедиции (Алексеева, 1965, 1973). Для материалов тех исследователей (К.Ю.Марк, В.М.Витов, М.С.Акимова, Т.Тот), для которых способы пересчета данных не были ранее разработаны, соответствующие коэффициенты коннексии к методическим приемам Т.И.Алексеевой были получены нами (Дерябин, 1998а).

Анализ групп населения, обследованных одним автором, во многом устраняет проблему методической несопоставимости данных. Правда, остается возможность того, что один и тот же исследователь, работающий несколько десятилетий, может бессознательно несколько модифицировать приемы определения вариантов описательных признаков (Алексеева, 1965; Schwidetzky, 1991).

Наиболее надежный способ коннексии может быть получен, если два исследователя проводили параллельные исследования одних и тех же индивидов в одно и то же время (Алексеева, 1965; Schwidetzky, 1991). Несколько менее надежным оказывается сопоставле-ние результатов обследования одних и тех же групп населения, сделанных в разное время. Наименее надежной является опосредованная коннексия, когда коэффициенты пересчета к некоторому стандарту находятся так, что за образец берутся оценки, которые сами подвергались коннексии.

Нами использовался в основном второй способ. При этом внимание обращалось на сопоставимость двух выборок, полученных разными авторами. Коннексия по нескольким описательным признакам считалась возможной, если две выборки взяты на одной и той же (или на очень близкой) территории и эти выборки оказывались очень близкими по измерительным показателям и по таким антропоскопическим характеристикам как цвет глаз и волос, где используются хорошо разработанные стандартные шкалы вариантов. В таких случаях расхождение по нескольким описательным характеристикам может быть в основном отнесено не за счет возможных антропологических различий, а считаться отражающим методическую сторону дела.

С учетом подобных соображений были получены коэффициенты коннексии данных М.Г.Абдушелишвили и А.Г.Гаджиева к некоторому единому стандарту, за который в нашем исследовании были приняты методические приемы Г.Ф.Дебеца, длительное время проводившего исследования населения Кавказа и осуществлявшего руководство аналогичными работами других авторов, проводившихся в этом регионе. В частности, Г.Ф.Дебецу принадлежат материалы по народам Дагестана и Афганистана. Кроме этого, большая часть данных по признакам описательной программы во время исследования на-

- 5 -

Таблица 1. Коэффициенты коннексионного пересчета

данных разных авторов

Признаки	М.Г.Абдушелишвили к Г.Ф.Де-бецу	А.Г.Гаджи-ев к Г.Ф.Дебецу	М.Г.Абдушелишвили к Н.Н.Че-боксарову	Т.Тот к В.Д.Дячен-ко
Рост бороды	0.00	0.00	+0.29	+0.10
Горизонтальн. профиль лица	-0.16	-0.11	-0.24	-0.40
Высота переносья	0.00	+0.37	+0.13	-
Кончик носа	-0.14	-0.37	+0.13	+0.09
Доля вогнутых профилей спинки носа	*1.00	*0.51	*0.67	*1.50
Доля выпуклых профилей спинки носа	*1.25	*0.68	*1.62	*1.60
Профиль верхней губы	+0.30	0.00	-0.46	0.00
Развитие надбровья	0.00	-0.08	0.00	-
Наклон лба	0.00	-0.34	0.00	-
Доля прямых волос	*1.04	*0.83	-	-

Примечание: для средних баллов поправка вносится прибавлением (+) или вычитанием (-) коэффициента, для долевых показателей - умножением (*)

селения Азербайджана была добыта либо самим Г.Ф.Дебецем, либо хорошо сконнексирована с его приемами (Касимова, 1975). Аналогичным образом, перед их опубликованием соответствующие поправки были внесены в данные А.Н.Пуляноса (1961) по грекам-уроженцам разных районов Греции и соседних территорий. Наконец, то обстоятельство, что Ю.Г.Рычков участвовал в работах, проводившихся Г.Ф.Дебецем в Дагестане (Дебец, 1956), делает весьма вероятной достаточную методическую сопоставимость данных Ю.Г.Рычкова по группам Западного Памира.

Коннексионные коэффициенты для методических приемов, используемых М.Г.Абду-шелишвили были получены при сопоставлении грузин-имеретин района Цхалтубо, обследованных Г.Ф.Дебецем (1956) с самтредскими и ткибульскими имеретинами М.Г.Абду-шелишвили. Эти выборки относятся к соседним географическим пунктам и обнаруживают хорошее соответствие по измерительной программе и по характеристикам пигментации глаз и волос. Поэтому, можно полагать, что некоторые небольшие несовпадения в средних баллах горизонтального профиля лица, положения кончика носа, профиля верхней губы и встречаемости выпуклого профиля спинки носа относятся именно к методическим расхождениям, для которых можно найти поправочные коэффициенты (табл.1). Коннексия данных А.Г.Гаджиева к стандарту приемов Г.Ф.Дебеца может быть проведена по группам ботлихцев, годоберинцев, каратинцев и андийцев, обследованных каждым из авторов в одних и тех же населенных пунктах (табл.1). В результате все четыре серии данных по народам Кавказа (Дебец, 1956; Абдушелишвили, 1964; Гаджиев, 1971; Касимова, 1975) могут быть приведены к единому стандарту.

- 6 -

При сравнительном анализе данных по народам Кавказа и групп населения Афганистана проблема сопоставимости не играет большой роли, так как последняя серия данных была получена Г.Ф.Дебецем. Правда, остается возможность того, что один и тот же исследователь, работающий несколько десятилетий, может бессознательно несколько модифицировать приемы определения вариантов описательных признаков (Алексеева, 1965; Schwidetzky, 1991).

Сопоставимые материалы по населению Индии были собраны двумя авторами: Н.Н.Че-боксаровым (1980) и М.Г.Абдушелишвили (1980, 1982). Здесь возможности коннексии были менее надежными, так как приблизительно сравнимыми оказались по две выборки: джатов и гуджаров, обследованные двумя авторами, что и позволило получить коннекси-онные коэффициенты, которые, конечно, имеют в какой-то степени условный характер (табл.1). Как указывает Т.И.Алексеева (1965), методические приемы Н.Н.Чебоксарова и Г.Ф.Дебеца могут считаться очень близкими, что, по-видимому, позволяет данные по на-селению Индии, приведенные к стандарту первого исследователя, использовать без до-полнительных поправок.

При сравнительном анализе населения Восточной Европы и Кавказа мы использовали стандарт Русской антропологической экспедиции, базирующийся на методических приемах Т.И.Алексеевой с использованием опубликованных (Алексеева, 1965, 1973) и полученных нами (Дерябин, 1998а) коннексионных коэффициентов. Данные для населения Кавказа приводились к этому стандарту с использованием рекомендаций Т.И.Алексеевой (1965). Правда, для материалов Т.Тота пришлось использовать наименее методически надежный опосредованный пересчет с предварительной коннексией к стандарту В.Д.Дя-ченко (табл.1), для чего сравнивались данные по обследованным Т.Тотом (1974) матолч-ским и асамоским венграм, проживающим на востоке Венгрии, и венграм береговским, данные по которым были получены В.Д.Дяченко (1965). После проведения этой операции материалы Т.Тота по венграм пересчитывались к стандарту Т.И.Алексеевой.

Разумеется, методика внесения коннексии не может считаться абсолютно точной. Однако, как это показали проведенные нами (Дерябин, 1998а) эксперименты, неполное (даже в половину коэффициентов пересчета) отражение методических расхождений авторов при проведении коннексии влияет на результаты канонического анализа не слишком существенно. Последнее позволяет надеяться на то, что коннексионные коэффициенты, не полностью учитывающие методические расхождения разных авторов, не внесут заметных артефактов в результаты, полученные с применением канонического анализа. Правда, подобный эффект может ожидаться только для анализа межгрупповой вариации достаточно большой величины. В ситуации рассмотрения тонких антропологических деталей, когда размах значений канонических переменных для исследуемых популяций составит около 1 внутригруппового среднего квадратического отклонения канонических переменных, несовершенство приемов коннексии может заметно исказить реально существующую картину. Для этих случаев лучше использовать данные, собранные одним автором.

* * *

В соответствии с поставленной нами задачей объективного изучения антропологической вариации, проявляющейся в населении Кавказа и соседних регионов, очень большое

- 7 -

значение приобретает выбор адекватной методики биометрического анализа данных. Главным, по нашему мнению, требованием, предъявляемым к ней, должно является отсутствие у применяемых приемов эффекта "наложения" свойств самих этих подходов на получаемую картину. Несоблюдение этого требования может приводить к артефактам результатов. Вообще говоря, наличие подобных желательных свойств метода анализа данных гарантировано отнюдь не всегда.

Например, часто применяемый на практике кластерный анализ по своей сути направлен на выявление дискретной структуры рассматриваемых данных и представление ее в виде набора тем или иным способом организованных кластеров. Но при использовании этого вида анализа часто забывают о том, что кластеризация целесообразна только там, где действительно в самих данных имеется дискретная структура. Если это условие выполняется, то кластерный анализ с той или иной степенью точности может эту структуру выявить. Однако, если данные представляют скорее непрерывную клинальную вариацию, когда объективная дискретность не проявляется, а один вариант через множество тонких переходов трансформируется - в другой, кластерный анализ по своим свойствам не может быть обоснованно применен (Козинцев, 1980). Правда, его использование в случаях, когда в данных существует непрерывная вариация, все равно приведет к выявлению какой-то кластерной структуры, но эти результаты окажутся статистическими артефактами (Дерябин, 1990) - примером наложения свойств метода, неадекватного данной ситуации, на объективно существующие закономерности изменчивости. С такой возможностью всегда следует считаться.

Другой ситуацией подобной неадекватности аппарата анализа данных может являться применение интерполяционной географической методики (Балановская и др., 1994, 1994а; Балановская, Нурбаев, 1995, 1996, 1997), которая априорно требует наличия в самих данных именно непрерывной клинальной вариации. В такой ситуации эта математически очень хорошо разработанная методика может выявить существование системы градиентов, вдоль которых происходят постепенные изменения уровня значений исходных признаков или их комплексов. Однако при объективном отсутствии клинальности и наличии в данных дискретной структуры, интерполяционные методы сгладят объективно существующие разрывы постепенности и выявят систему клин, многие из которых окажутся артефактами - результатами наложения качеств самого применяемого метода на реальную картину вариации.

Аналогичными свойствами отличается пространственная автокорреляционная методика (Sokal, Oden, 1978), с использованием которой была осуществлена, в частности, серия антропологических исследований населения Европы (Sokal, Uytterschaut, 1987; Sokal, Winkler, 1987; Sokal, Harding, Oden, 1989). Она специально направлена на поиски градиентов, соответствующих клинальной вариации. Для ситуаций объективного существования непрерывных пространственных закономерностей антропологической изменчивости автокорреляционные методики хорошо опишут их, но в противном случае существования пространственно хорошо разделенных расовых вариантов окажутся бессильными.

В отличие от двух крайних описанных ситуаций такие методы визуализации данных как компонентный и канонический анализы или многомерное шкалирование, не требуют априорной информации о клинальности или дискретности структуры исследуемой вариации. Их цель - в выявлении и наглядном представлении таксономической картины с воз-

- 8 -

можным присутствием в ней и клинальных и дискретных закономерностей. Правда, наиболее популярный и часто используемый метод главных компонент не может обоснованно применяться при анализе межвыборочной вариации, что следует из его математических свойств. В соответствии с основными посылками компонентного анализа предполагается существование только одного уровня изменчивости, для которого следует найти закономерности вариации и коррелированности признаков. Иными словами, он в соответствии с своими свойствами предназначен для рассмотрения внутригрупповой вариации, изучаемой в однородных группах населения, когда единицей исследования оказывается индивид.

Вместе с тем, любые межгрупповые исследования предполагают наличие по меньшей мере двух уровней изменчивости с принципиально различными направлениями вариации: физиологическими - для внутригруппового межиндивидуального компонента и историческими - для межгрупповой части. Если первый уровень для признаков, используемых в расоведении, характеризуется значительной устойчивостью (Дерябин, 1997) и независимостью от расовой принадлежностью групп населения, то второй - полностью зависит от изучаемых расовых контрастов. Использование компонентного анализа для изучения межгрупповой вариации, когда наборы средних величин для разных признаков считаются как бы соответствующими наборам величин признаков у индивидов, по существу означает, что исследователь сознательно закрывает глаза на факт внутригрупповой вариации, допуская тем самым, как нам представляется, недопустимый произвол. Но можно ли представить себе ситуацию, когда компонентный анализ межгрупповой корреляционной матрицы, найденной по средним величинам, даст совершенно те же самые результаты, что и математически корректный канонический анализ? Для этого случая требуется (Seal, 1966) соблюдение двух условий. Во-первых, внутригрупповые корреляции все признаков должны быть нулевыми. Во-вторых, должно соблюдаться равенство межгрупповых и внутригрупповых дисперсий для всех признаков. Но последнее условие означает полное отсутствие неслучайной межгрупповой вариации. Иными словами, два метода анализа дадут одинаковые результаты лишь в ситуации, когда никакой межгрупповой вариации наблюдаться не будет, а рассмотрению будет подвергаться внутригрупповая вариабельность. Эмпирическая проверка работоспособности главных компонент по сравнению с более корректными здесь каноническим анализом и многомерным шкалированием, которая была проведена нами (Дерябин, 1997а, 1998б) продемонстрировала существование заметных и закономерных расхождений результатов компонентного анализа таксономической вариации различного ранга по сравнению с картинами, получаемыми посредством канонического анализа или многомерного шкалирования, тогда как два последних метода давали практически идентичные результаты. Аналогичным образом, в краниологическом исследовании Р.Сокэла и др. (Sokal et al., 1987) многомерное шкалирование дало лучшие результаты по сравнению с главными компонентами. Иными словами, компонентный анализ межгрупповой вариации часто дает картину, многие свойства которой трудно расценивать иначе чем статистические артефакты. Это обстоятельство не позволяет считать компонентный анализ подходящим методом изучения межгрупповой вариации.

Корректный при использовании для рассмотрения межгрупповой вариации канонический или множественный дискриминантный анализ (Seal, 1964; Бартлетт, 1968; Blackith, Reyment, 1971; Дерябин, 1983; Аренс, Лейтер, 1985) можно считать математическим раз-

- 9 -

витием классических взглядов Е.М.Чепурковского (Tschepourkowsky, 1905). Здесь при одновременном рассмотрении межгрупповых и внутригрупповых коэффициентов корреляции и дисперсий признаков выявляются основные закономерности межгрупповой вариации, свободные от влияния аналогичных внутригрупповых направлений изменчивости и описываемые новыми признаками, которые называются каноническими переменными (или дискриминаторами) K_i

K_i = c_1i M₁ + c_2i M₂ + ... + c_mi M_m , (1)

где M_j - средние величины исходных признаков, c_ji - некоторые вычисляемые коэффици-енты. Все найденные канонические переменные - нескоррелированы ни в межгрупповом, ни во внутригрупповом планах. Внутригрупповые дисперсии у всех этих новых признаков равны единице, а межгрупповые - различны, так что можно говорить о более важных и менее важных закономерностях таксономической вариации. Каждая каноническая переменная имеет максимальное соотношение своей межгрупповой и внутригрупповой вариации и является, таким образом, признаком максимально хорошо выявляющим существующую таксономическую изменчивость.

Для любой канонической переменной можно получить значение у любого наблюдения в любой группе населения или вычислить среднюю арифметическую величину в этой группе. Такие средние величины могут наноситься на географические карты, различные графики и т. д., что делает выявляемые многомерные закономерности межгрупповой вариации наглядными и доступными для визуального рассмотрения и истолкования.

Многомерное шкалирование до некоторой степени логически родственно методам кластерного анализа (Терехина, 1986; Дэйвисон, 1988). В обоих случаях рассматриваются одни и те же матрицы показателей таксономического сходства или различия, дающие представления о близости изучаемых единиц между собой. Однако, в дальнейшем информация, содержащаяся в этих матрицах, делается наглядной с применением существенно различных методических подходов.

Кластерный анализ на основе данных о взаимных расстояниях с применением относительно несложных вычислений жестко и достаточно однозначно выделяет группы таксономических единиц, расстояния между которыми относительно невелики. Визуально ход анализа и его результаты обычно представляются в виде дендрограммы. Вид этой дендрограммы часто может существенно зависеть от выборочных случайностей и от примененной процедуры выявления кластеров.

Многомерное шкалирование направлено на достижение иного результата - наглядного представления всех расстояний между исследуемыми единицами в пространстве малого числа (обычно 2 - 3) измерений. При этом получаются дву- или трехмерные графики расположения исследуемых выборок так, чтобы наглядно наблюдаемые на них расстояния между точками, представляющими анализируемые единицы, были бы максимально подобными эмпирически найденным расстояниям. Суждение о наблюдаемой таксономической структуре производится визуально, и в этом отношении многомерное шкалирование родственно каноническому или компонентному анализам.

Цель многомерного шкалирования достигается обычно в ходе получения ряда последовательных приближений набора наблюдаемых на графике расстояний к эмпирически вычисленным. Процесс завершается при достижении минимально возможных суммарных различий этих двух типов расстояний между всеми парами рассматриваемых единиц.

– 10 -

Наилучшие результаты обычно получаются с применением так называемого неметрического шкалирования, которое накладывает меньше строгих ограничений на соотношения наблюдаемых и эмпирических расстояний.

Степень суммарных различий двух типов расстояний описывается так называемой величиной стресса. Многомерное шкалирование считается успешным, если стресс имеет до-пустимо малую величину (обычно - меньше 0.10 или 0.15). В этом случае по координатам точек, соответствующих изучаемым единицам, можно построить дву- или трехмерный график, который и является результатом многомерного шкалирования.

Результаты многомерного шкалирования по сравнению с кластеризацией лишены жесткой нацеленности на окончательное выявление объединений с точностью до самой последней рассматриваемой единицы. Они просто предоставляют исследователю наглядную картину взаимного расположения всех объектов в соответствии с их эмпирическими расстояниями. Поэтому, многомерное шкалирование лишено описанных выше недостатков кластеризации. Действительно, если структура данных характеризуется непрерывным характером, то исследователь увидит соответствующую картину, лишенную дискретной структуры. В ситуации, когда некоторые выборки будут по своему статусу промежуточны-ми между какими-то антропологическими общностями, на графике многомерного шкали-рования эту промежуточность можно будет увидеть наглядно.

Справедливости ради следует отметить и недостаток многомерного шкалирования. Оно требует проведения весьма сложных вычислений, и в стандартных пакетах программ обычно невозможно одновременно рассматривать более чем от нескольких десятков до одной сотни единиц. При этом, канонический анализ с применением некоторых компьютерных программ может проводиться для нескольких тысяч (или даже десятков тысяч) выборок.

С учетом вышеизложенных соображений, в настоящей работе использовался вариант канонического анализа, позволяющий рассматривать одновременно количественные, балловые и бинарные признаки (Дерябин, 1991, 1995, 1998а).

* * *

Материалы для анализа извлекались из построенной автором базы данных, включающей информацию о средних арифметических величинах для количественных и балловых признаков, значениях долей бинарных показателей, величинах средних квадратических отклонений и объемов выборок для около 1900 выборок современного населения Евразии. В базе данных содержится информация для следующих признаков:

1) длины тела, 10) ширины носа,

2) продольного диаметра головы 11) высоты верхней губы,

3) поперечного диаметра головы 12) ширины рта,

4) наименьшей ширины лба, 13) толщины губ,

5) морфологической высоты лица 14) цвета кожи,

6) скулового диаметра 15) цвета глаз,

7) нижнечелюстного диаметра, 16) цвета волос,

8) высоты носа от бровей, 17) доли встречаемости светлых волос

9) высоты носа от переносья, 18) доли встречаемости темных волос

- 11 -

19) доли встречаемости прямых волос, 29) положения основания носа,

20) доли встречаемости жестких волос, 30) профиля верхней губы,

21) роста бороды, 31) доли отсутствия эпикантуса

22) роста волос на груди, 32) доли отсутствия складки

23) роста бровей, верхнего века,

24) горизонтального профиля лица 33) наклона лба,

25) высоты переносья, 34) развития надбровья

26) доли встречаемости вогнутых спинок носа, 35) головного указателя,

27) доли встречаемости выпуклых спинок носа, 36) лицевого указателя,

28) положения кончика носа, 37) носового указателя.

Для большего удобства работы с базой данных (формирование извлечений из нее, внесения коннексии в значения некоторых признаков и др.) в ней имеются ключевые поля, содержащие информацию:

1) названию выборки, 5) название языковой группы,

2) названию пункта наблюдения 6) данные об авторах обследовавших,

3) крупная рубрикация территории, к которой выборку,

относится выборка, 7) данные о публикации материалов

4) дробная рубрикация территории, к которой

относится выборка,

В зависимости от решаемой задачи из базы данных извлекается материалы, включающие информацию по необходимому набору групп населения и формируется промежуточный текстовый файл со значениями для них средних арифметических величин, средних баллов и долей, а также количества наблюдений. Эта информация затем импортируется в написанную автором программу КАНОКЛАС 6.0 (для MS DOS), которая осуществляет дальнейшую ее обработку с проведением канонического и кластерного анализов, а также неметрического многомерного шкалирования по методам Краскела и Гудмена.

.

< Esc = Выход >

Ввод данных Редактирование Наборы признаков Вычисления



< F1 - Помощь >

ВЫБЕРИТЕ ВАРИАНТ

Импортирование из базы данных.

Дополнение данных.

Ввод внутригрупповых средн. квадратическ.отклонений.

Ввод внутригрупповой корреляционной матрицы.

< Esc - Возврат >

Рисунок 1. Меню ввода данных для решения конкретной

задачи программы КАНОКЛАС 6.0

- 12 -

Программа КАНОКЛАС 6.0 организована в виде традиционной системы меню, из кото-рых основное - определяет выбор манипуляций с данными или переход к вычислениям. Для каждой из четырех позиций основного горизонтального меню имеется свое вертикальное меню. Выбор осуществляется перемещением курсорного указателя.

Ввод данных для решения конкретной задачи начинается с импортирования информации, содержащейся в промежуточном текстовом файле, полученном при формировании извлечения из базы данных (рис.1). При этом происходит формирование файлов данных программы КАНОКЛАС с возможностью произвольного доступа к любой выборке. При необходимости эти файлы могут быть дополнены информацией по небольшому количеству выборок путем ее ввода с клавиатуры в рамках самой программы без обращения к базе данных.

Для проведения вычислений требуются также стандартные значения внутригрупповых средних квадратических отклонений и коэффициентов корреляции, для чего в меню имеются соответствующие пункты в главном меню (рис.1). Данные по внутригрупповым средним квадратическим отклонениям содержатся в файлах самой программы. В частности, имеется возможность автоматической загрузки значений внутригрупповых "сигм", найденных усреднением по многим выборкам для:

1) русских,

2) украинцев,

3) славянских народов Восточной Европы,

4) народов Восточной Прибалтики,

5) народов севера Восточной Европы,

6) финских и тюркских народов восточно-европейской России,

7) народов Восточной Европы в целом,

8) народов Кавказа,

9) народов Восточной Европы и Кавказа,

10) народов Восточной Европы и Западной Сибири,

11) народов Западной Сибири,

12) народов Центральной и Восточной Сибири,

13) народов Сибири в целом,

14) народов Средней Азии,

15) народов Кавказа и Средней Азии,

16) народов Сибири и Средней Азии,

17) европеоидов и монголоидов в целом.

Необходимость располагать при вычислениях значениями внутригрупповых средних квадратических отклонений, найденными для населения конкретных регионов, связано с тем, что эти показатели для балловых и особенно бинарных признаков могут заметно зависеть от средних уровней значений признаков. Например, для средней зоны Восточной Европы цвет волос внутри каждой выборки может варьировать от белокурых и светло-русых до черно-каштановых, что приведет к увеличению соответствующего среднего квадратического отклонения. Однако, для южных европеоидов могут быть представленными в основном черно-каштановые и черные цвета, что значительно уменьшит внутригрупповую "сигму". Для бинарных признаков внутригрупповая вариация непосредственно зависит от доли встречаемости его вариантов.

- 13 -

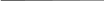< Esc = Выход >

Ввод данных Редактирование Наборы признаков Вычисления



< F1 - Помощь >

ВЫБЕРИТЕ ВАРИАНТ РЕДАКТИРОВАНИЯ ДАННЫХ

Редактирование средних величин и имен выборок.

Редактирование внутригрупповых средних квадратических

отклонений.

Редактирование внутригрупповой корреляционной матрицы.

< Esc - Возврат >

Рисунок 2. Меню редактирования данных в программе

КАНОКЛАС 6.0

Несколько проще оказывается ситуация с внутригрупповыми корреляциями. Специальная проверка, проведенная нами (Дерябин, 1997) показала, что использование единой внутригрупповой корреляционной матрицы расоводиагностических признаков для применения многих методов многомерной статистики является вполне допустимым. Ос-новные закономерности внутригрупповых корреляций здесь отличаются относительной устойчивостью, а некоторые межвыборочные различия не имеют расового характера. Более того, вычисление такой матрицы по нескольким выборкам может значительно ослабить многие влияния, искажающие внутригрупповые связи.

Поэтому, в файлах программы КАНОКОАС 6.0 имеется стандартная внутригрупповая корреляционная матрица, полученная усреднением для примерно 3400 наблюдений (При-ложение 2), относящихся к русским, коми, татарам-мишарям, армянам, азербайджанцам, аварцам, чеченцам, ингушам, ненцам, селькупам, хантам, манси, кетам, тунгусам, бурятам, калмыкам, гилякам, ульчам, киргизам, туркменам, таджикам (Дерябин, 1997). После обращения к соответствующему пункту меню (рис.1) для набора признаков, который анализируется в конкретной задаче из этой корреляционной матрицы автоматически извлекается необходимый блок, который направляется на вычисления - в соответствии с алгоритмом эта матрица подвергается процедуре Халецкого (Мэйдональд, 1988).

При работе с большими массивами информации даже при самом тщательном ее визуальном контроле почти неизбежными являются ошибки ввода, которые, как правило, имеют грубый характер. В программе КАНОКЛАС 6.0 имеется блок выявления таких ошибок при проведении канонического анализа. В связи с этим в основном меню имеется режим редактирования данных. Здесь можно обратиться к любой выборке и с клавиатуры внести необходимые исправления. Обращение к выборке осуществляется либо по ее номеру в анализируемой задаче, либо просмотром имен всех анализируемых единиц (названий национальной группы и географического ее пункта) и непосредственным выбором.

- 14 -

< Esc = Выход >

Ввод данных Редактирование Наборы признаков Вычисления



< F1 - Помощь >

ВЫБЕРИТЕ ВАРИАНТ ИЗМЕНЕНИЯ НАБОРА ПРИЗНАКОВ

Использовать для анализа часть набора признаков.

После проведения анализа части набора признаков

использовать другую такую часть.