
- •Предмет физики
- •Раздел 1. Физические основы механики.
- •Глава 1. Кинематика.
- •§1.1. Инерциальные системы отсчета. Принцип относительности.
- •§1.2. Кинематика поступательного и вращательного движений.
- •§1.3. Закон (кинематическое уравнение) движения
- •§1.4. Скорость
- •§1.5. Ускорение
- •§1.6. Равномерное и равнопеременное движения.
- •§ 1.7. Связь между линейными и угловыми кинематическими характеристиками.
- •§ 1.8. Краткие итоги главы 1.
- •§ 1.9. Примеры
- •Глава 2. Динамика
- •§2.1. Задача динамики. Динамические характеристики
- •§2.2. Виды сил.
- •§2.4. Момент инерции.
- •§2.5. Момент силы.
- •§2.6. Уравнение динамики
- •§2.7. Итоги главы 2.
- •П римеры
- •Глава 3. Законы сохранения в механике.
- •§ 3.1.Фундаментальный характер законов сохранения
- •§ 3.2. Закон сохранения импульса.
- •§3.3.. Работа силы. Мощность.
- •§ 3.4. Механическая энергия.
- •§ 3.5. Закон сохранения механической энергии
- •§ 3.6. Столкновения тел
- •§ 3.5. Закон сохранения момента импульса
- •§ 3.6. Итоги главы 3
- •Примеры
- •Глава 4. Элементы специальной теории относительности
- •§ 4.1. Закон сложения скоростей. Постулат о скорости света
- •§ 4.2. Релятивистское сокращение длины и замедление времени
- •§ 4.3. Релятивистская динамика
- •Примеры
- •Раздел 4. Электромагнетизм
- •Глава 5. Электростатика
- •§ 5.1.Электрический заряд. Закон Кулона.
- •§5.2. Электрическое поле. Напряженность.
- •§ 5.3. Теорема Гаусса.
- •§ 5.4. Потенциал и работа электростатического поля.
- •§ 5.5. Связь напряженности и потенциала электростатического поля.
- •§ 5.6. Электростатическое поле в веществе.
- •§ 5.7. Электроемкость. Конденсатор.
- •§ 5.8. Энергия электрического поля.
- •Глава 6. Постоянный электрический ток.
- •§ 6.1. Электрический ток: сила тока, плотность тока
- •§ 6.2. Механизм электропроводности
- •§ 6.3. Законы постоянного тока.
- •§ 6.4. Работа и мощность тока
- •Глава 7. Магнитное поле тока
- •§ 7.1 Магнитное взаимодействие. Магнитное поле
- •§ 7.2. Закон Био-Савара-Лапласа
- •§ 7.3. Вихревой характер магнитного поля.
- •§ 7.4. Действие магнитного поля на токи и движущиеся электрические заряды
- •§ 7.5. Магнитное поле в веществе
- •Глава 8. Явление электромагнитной индукции
- •§ 8.1. Основной закон электромагнитной индукции
- •§ 8.2. Самоиндукция и взаимная индукция
- •§ 8.3. Энергия магнитного поля
- •§ 8.4. Вихревое электрическое поле. Уравнения Максвелла
§ 4.2. Релятивистское сокращение длины и замедление времени
Вернемся к формуле (4.1.1) сложения скоростей. Пусть движущейся системой отсчета является поезд. В момент, когда хвостовой вагон поезда поравнялся с телеграфным столбом, из этого вагона послан световой сигнал машинисту. Через промежуток времени ∆t ′ машинист зарегистрирует этот сигнал, и если длина поезда ∆l′, то скорость света в движущейся системе отсчета с =∆l′/∆t ′. Предположим, что за этим же самым процессом наблюдает стрелочник, стоящий на насыпи. Обозначим измеренное им время ∆t . Чтобы определить скорость света, он также должен разделить путь, пройденный светом, на время прохождения. Что же касается пути, пройденного светом, то с точки зрения стрелочника он состоит из длины поезда ∆l и расстояния, на которое успеет хвостовой вагон за время ∆t удалиться от телеграфного столба. Если скорость поезда υ0, то это расстояние составит υ0∆t. Итак, с точки зрения стрелочника скорость света с =(∆l+υ0∆t)/∆t=∆l /∆t + υ0. Согласно постулату о скорости света ∆l′/∆t ′=∆l /∆t + υ0. Очевидно, что полученное равенство выполняется только при условии ∆l′ > ∆l или ∆t ′<∆t, т.е. с точки зрения стрелочника поезд стал короче или что время в нем идет медленнее. Опыт показывает, что имеют место оба этих фактора.
Размеры тел в направлении движения сокращаются. Если размер покоящегося тела в некотором направлении равен l, то при движении тела в этом направлении со скоростью υ он уменьшится до величины
l′=
l![]() (4.2.1)
(4.2.1)
Этот эффект называется лоренцевым сокращением длины и свидетельствует о зависимости пространственных соотношений от движения, т.е. об относительности пространства. Размеры тел в направлении, поперечном движению, не изменяются.
Движущиеся часы идут медленнее покоящихся часов. Если промежуток времени между двумя какими - либо последовательными событиями по покоящимся часам равен ∆t, то по движущимся часам он будет меньше и равен
∆t ′=∆t (4.2.2)
Этот эффект называют лоренцевым замедлением времени. Он свидетельствует о том, что течение времени не является абсолютным и зависит от движения.
Лоренцево сокращение длин и промежутков времени является следствием всеобщих свойств пространства и времени. При релятивистских движениях пространство и время оказываются не абсолютными и независимыми друг от друга категориями, а относительными и взаимосвязанными, образуя единую категорию, именуемую ″пространство-время″. Время, отсчитываемое неподвижными часами, называется собственным. Собственными также называются размеры тела в системе отсчета, где оно покоится. Формулы (4.2.1) и (4.2.2) свидетельствуют о том, что течение собственного времени является наиболее медленным, а собственные размеры являются максимальными. Релятивистское замедление времени не только наблюдается в опыте, но и используется в ускорительной технике для получения пучков нестабильных элементарных частиц, таких как пионы и каоны. Собственное время жизни этих частиц порядка 10-8 с, что позволяет им пройти расстояние около 3 м. Если же частица движется со скоростью 0,995 с, то лабораторное время ее жизни составляет 10-7 с. За такое время частица успевает пройти около 30 м, и этого расстояния достаточно, чтобы в ускорителе отделить пучок нужных частиц от прочих и разместить необходимые измерительные приборы.
Релятивистская формула сложения скоростей в простейшем случае одномерного движения имеет вид:
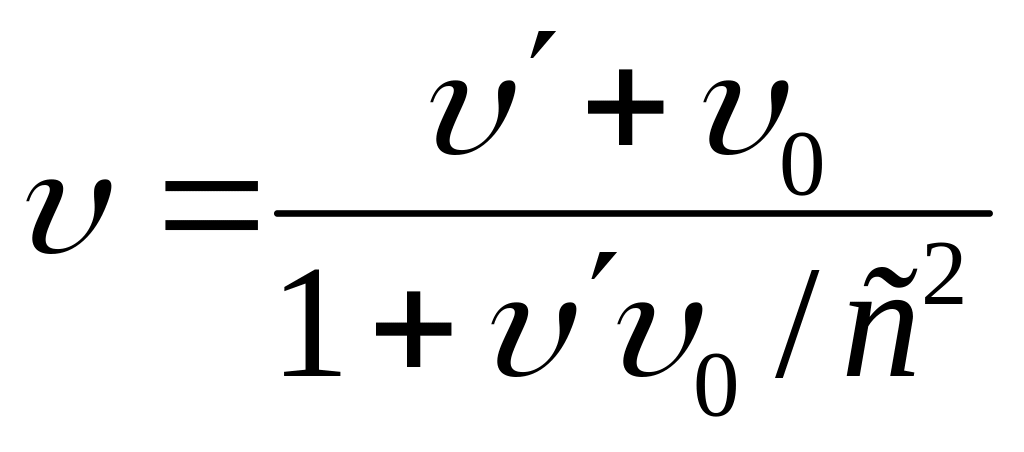 (4.2.3)
(4.2.3)
Здесь
-
скорость движения одной инерциальной
системы отсчета (назовем ее движущейся)
относительно другой (неподвижной).
![]() и
и
![]() -
скорости движения тела в движущейся и
неподвижной системах отсчета
соответственно, при этом все три скорости
направлены вдоль одной оси. Самостоятельно
убедитесь в том, что формула (4.2.3) не
противоречит постулату о скорости
света.
-
скорости движения тела в движущейся и
неподвижной системах отсчета
соответственно, при этом все три скорости
направлены вдоль одной оси. Самостоятельно
убедитесь в том, что формула (4.2.3) не
противоречит постулату о скорости
света.
