Обращенные формы.

Рис. 12.8.

В теории линейных направленных сигнальных графов существуют процедуры преобразования исходных графов с сохранением передаточных функций. Одна из таких процедур - обращение (транспозиция) графов, которая выполняется путем изменения направления всех ветвей цепи, при этом вход и выход графа также меняются местами. Для ряда систем такая транспозиция позволяет реализовать более эффективные алгоритмы обработки данных. Пример обращения графа прямой канонической формы рекурсивной системы (с перестроением графа на привычное расположение входа с левой стороны) приведен на рис. 12.8.

1.13 Фильтры Чебышева

Отличительной чертой фильтров Чебышева является наимень­шая величина максимальной ошибки аппроксимации в заданной полосе частот. В действительности ошибка аппроксимации представляется в заданной полосе равновеликими пульсациями, т. е. она флуктуирует между максимумами и минимумами равной ве­личины. В зависимости от того, где минимизируется ошибка аппрок­симации — в полосе пропускания или в полосе непропус- кания,— различают фильтры Чебышева типа I и II.

Фильтры Чебышева типа I имеют только полюсы и обеспечивают равновеликие пульсации амплитудной характеристики в полосе пропускания и монотонное изменение ослабления в полосе не­пропускания. Квадрат амплитудной характеристики фильтра Чебышева типа I n-го порядка описывается выражением

(13.1)

где T_n(Ω)- полином Чебышева n-го порядка, по определению равный:

(13.2)

а - параметр, характеризующий пульсации в полосе пропускания.

Свойство оптимальности фильтров Чебышева типа I порядка n заключается в том, что не существует какого-либо другого фильт­ра n-го порядка, содержащего только полюсы, который имел бы та­кие же или лучшие характеристики и в полосе пропускания, и в полосе непропускания. Другими словами, если какой-либо фильтр n-го порядка, содержащий только полюсы, имеет в полосе пропускания лучшие характеристики по сравнению с фильтром Чебышева типа I порядка n, то в полосе непропускания характе­ристики этого фильтра наверняка будут хуже, чем у фильтра Чебышева.

Фильтры Чебышева типа II (иногда их называют также обрат­ными фильтрами Чебышева) обеспечивают монотонное изменение ослабления в полосе пропускания (максимально гладкое при Ω = 0) и равновеликие пульсации в полосе непропускания. Нули фильтров этого типа располагаются на мнимой оси в s-плоскости, а полюсы — в левой полуплоскости. Квадрат амплитудной харак­теристики фильтров Чебышева типа II порядка n можно предста­вить следующим образом:

(13.3)

где Ω_r — наинизшая частота, на которой в полосе непропускання достигается заданный уровень ослабления.

На рис. 13.1 показано поведение квадрата амплитудной харак­теристики для фильтров Чебышева типа I и II при четных и нечет­ных n. Во всех этих фильтрах граница полосы пропускания нахо­дится при Ω = 1, где | H (1) |² = 1/(1 + ²), а граница полосы не­пропускания расположена при Ω = Ω_r, где | H (Ω_r) |² = 1/A² .

Фильтр Чебышева типа I имеет простые полюсы в точках , где k = 1, 2,..n, которые лежат в s-плоскости на эллипсе, уравнение которого имеет вид:

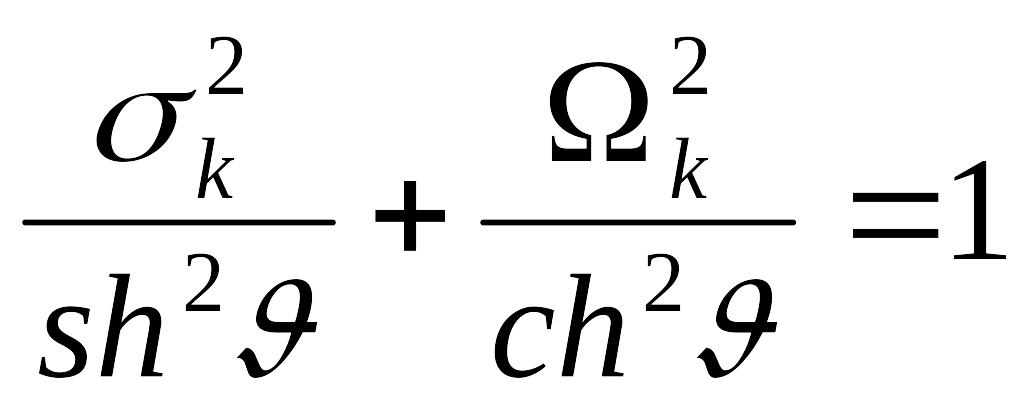(13.4)

Здесь

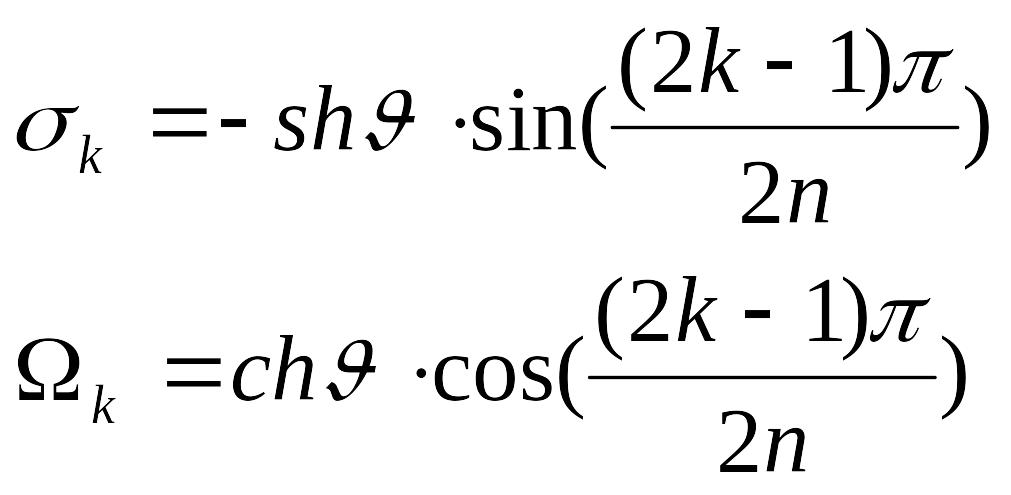(13.5)

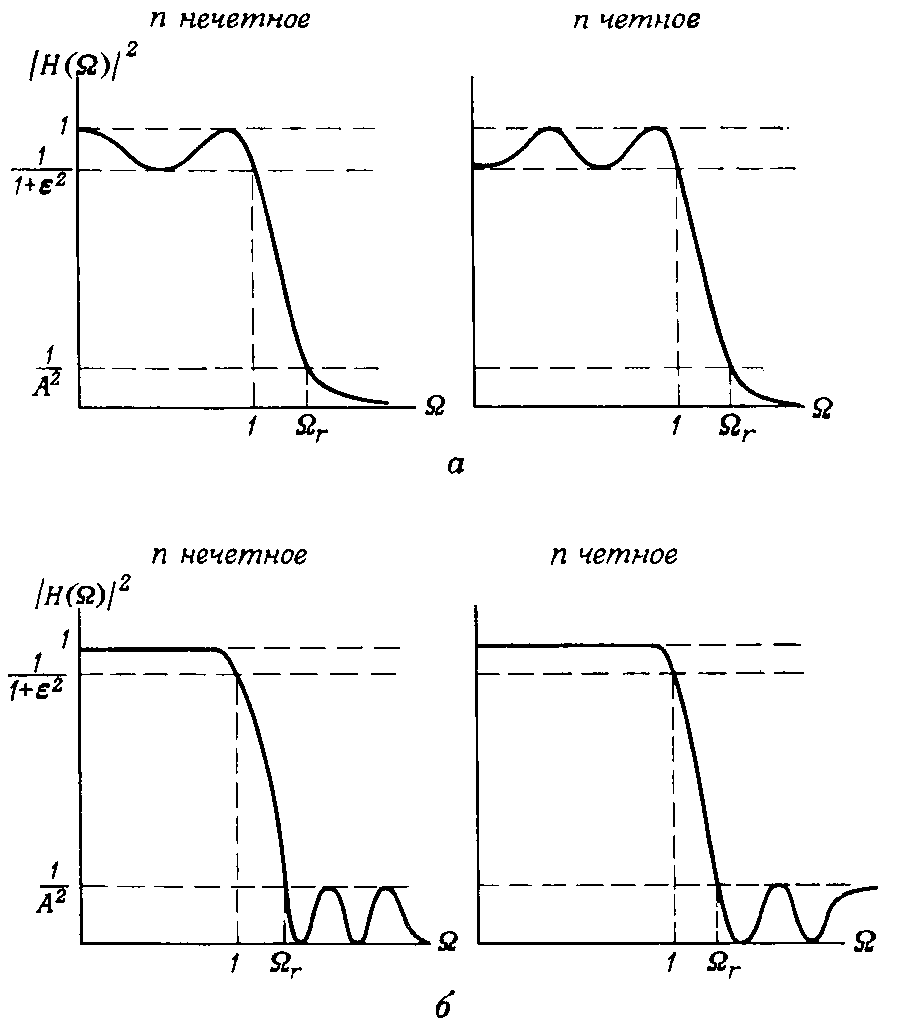
Рис.13.1. Общий вид функции квадрата амплитудной характеристики аналоговых фильтров Чебышева нижних частот типа I и II.

а — фильтр Чебышева типа I;

б — фильтр Чебышева типа II.

(13.6)

и

(13.7)

Фильтры Чебышева типа I I имеют и полюсы, и нули. Нули являются чисто мнимыми и находятся в точках:

, где k =1,2…..n. (13.8)

(Отметим, что при нечетных п нуль с номером k == (n +1)/2 находится на бесконечности.) Полюсы фильтров типа II можно найти, вычислив координаты особых точек знаменателя передаточ­ной функции.

Простые преобразования дают для полюсов (k = 1, 2, ...) следующие выражения:

(13.9)

где

(13.10)

причем

(13.11)

и

(13.12)

Фильтры Чебышева типа I и II полностью определяются лю­быми тремя из следующих четырех параметров:

1) n (порядок фильтра);

2) (параметр, характеризующий пульсации в полосе про­пускания, см. рис. 13.1);

3) (наинизшая частота, на которой в полосе непропуска­ния достигается заданное ослабление, см. рис. 13.1);

4) А (параметр, характеризующий ослабление в полосе непро­пускания, см. рис. 13.1).

Порядок фильтра Чебышева n, необходимый для обеспечения

заданных значений , А и , определяется с помощью формулы

(13.13)

где

(13.14)

Пример 2. Рассчитать фильтр Чебышева минимального порядка, удовлетво- ряющий следующим условиям:

-пульсации в полосе пропускания равны 2 дБ;

-переходное отношение ;

ослабление в полосе непропусканпя 30 дБ.

Решение. Используя рис. 13.1, найдем параметры фильтра , А и по заданным характеристикам

Затем по формуле (13.14) получим g = 41,33, а по формуле (13.13) вычислим значение n = 6,03.

На рис. 4.19 и 4.20 представлены основные характеристики (амплитудная в логарифмическом масштабе, фазовая и групповой задержки) фильтров Чебышева типа I и II, удовлетворяющие ус­ловиям, перечисленным в примере 2. Оба фильтра имеют частоту среза = 1000 рад/с (т. е. == 5000 Гц). Из сопоставления рис. 4.19 и 4.20 видно, что поведение характеристики группо­вой задержки в полосе пропускания для фильтра типа II вообще значительно лучше, чем для фильтра типа I. Это связано с тем, что нули фильтров Чебышева типа II располагаются в s-плоскости на оси jΩ, тогда как все нули фильтров Чебышева типа I находят­ся на бесконечности.