
- •2.4.3 Ацп с плавающей точкой……………………………………………
- •1 Цифровые фильтры
- •1.1 Явление Гиббса
- •1.1.1 Сущность явления Гиббса
- •1.1.2 Параметры эффекта
- •1.1.3 Последствия для практики
- •1.2 Весовые функции
- •1.2.1 Нейтрализация явления Гиббса в частотной области
- •1.2.2 Основные весовые функции
- •1.3 Типы фильтров
- •1.4 Разностное уравнение
- •Нерекурсивные фильтры
- •1.5.1 Методика расчетов нцф
- •1.5.2 Идеальные частотные фильтры
- •1.5.3 Конечные приближения идеальных фильтров
- •1.5.3.1 Применение весовых функций
- •1.5.3.2 Весовая функция Кайзера
- •1.5.4 Дифференцирующие цифровые фильтры
- •1.5.5 Гладкие частотные фильтры
- •1.6 Рекурсивные фильтры
- •6.3 Интегрирующий рекурсивный фильтр.
- •1.6.1 Принципы рекурсивной фильтрации
- •1.6.2 Режекторные и селекторные фильтры
- •1.6.2.1 Комплексная z-плоскость.
- •1.6.2.2 Режекторные фильтры
- •1.6.2.3 Селекторный фильтр
- •1.6.3 Билинейное z-преобразование
- •1.6.4 Типы рекурсивных частотных фильтров
- •1.7 Импульсная характеристика фильтров
- •Передаточные функции фильтров
- •1.9 Частотные характеристики фильтров
- •1.10 Частотный анализ цифровых фильтров
- •1.10.1 Сглаживающие фильтры и фильтры аппроксимации
- •1.10.1.1 Фильтры мнк 1-го порядка (мнк-1)
- •1.10.1.2 Фильтры мнк 2-го порядка (мнк-2)
- •1.10.1.3 Фильтры мнк 4-го порядка
- •1.10.2 Разностные операторы
- •1.10.2.1 Разностный оператор
- •1.10.2.2 Восстановление данных
- •1.10.2.3 Аппроксимация производных
- •1.10.3 Интегрирование данных
- •1.10.4 Расчёт фильтров по частотной характеристике
- •1.11 Фильтрация случайных сигналов
- •1.12 Структурные схемы цифровых фильтров
- •Обращенные формы.
- •1.13 Фильтры Чебышева
- •1.14 Фильтры Баттерворта
- •Свойства фильтров Баттерворта нижних частот:
- •1.15 Фильтры Бесселя
- •2 Аналого-цифровое преобразование
- •2.1 Цифровая обработка звуковых сигналов
- •2.2 Основы аналого-цифрового преобразования
- •2.2.1 Основные понятия и определения
- •2.3 Структура и алгоритм работы цап
- •Контрольные вопросы
- •2.4 Структура и алгоритм работы ацп
- •2.4.1 Параллельные ацп
- •2.4.2 Ацп с поразрядным уравновешиванием
- •2.4.3 Ацп с плавающей точкой
- •Контрольные вопросы
- •Глава 3. Звук.
- •3.1 Аудиосигнал
- •3.1.1 Звуковые волны
- •3.1.2 Звук как электрический сигнал
- •3.1.3 Фаза
- •3.1.4 Сложение синусоидальных волн
- •3.2 Звуковая система
- •3.2.1 Назначение звуковой системы
- •3.2.2 Модель звуковой системы
- •3.2.3 Входные датчики
- •3.2.4 Выходные датчики
- •3.2.5 Простейшая звуковая система
- •3.3 Амплитудно-частотная характеристика
- •3.3.1 Способы записи ачх в спецификации звуковых устройств
- •3.3.2 Октавные соотношения и измерения
- •3.3.3 Ачх реальных устройств воспроизведения звука
- •3.3.4 Диапазон частот голоса и инструментов
- •3.3.5 Влияние акустических факторов
- •3.4 Единицы измерения, параметры звуковых сигналов
- •3.4.1 Децибел
- •3.4.2 Относительная мощность электрических сигналов дБm
- •3.4.3 Децибелы и уровень звука
- •3.4.5 Громкость, уровень сигнала и коэффициент усиления
- •3.4.6 Громкость
- •3.5 Динамический диапазон
- •3.5.1 Запас динамического диапазона
- •3.5.2 Выбор динамического диапазона для реальной звуковой системы
- •3.6 Цифровой звук
- •3.6.1 Частота дискретизации
- •3.6.2 Разрядность
- •3.6.3 Дизеринг
- •3.6.4 Нойс шейпинг
- •3.6.5 Джиттер
- •3.7 Методы и стандарты передачи речи по трактам связи, применяемые в современном оборудовании (7 кГц)
- •3.7.1 Импульсно-кодовая модуляция (pcm — Pulse-Code Modulation)
- •3.7.3 Помехоустойчивость методов икм
- •3.7.4 Методы эффективного кодирования речи
- •3.7.5 Кодирование речи в стандарте cdma
- •3.7.6 Речевые кодеки для ip-телефонии
- •3.7.7 Оценка качества кодирования речи
- •3.8 Общие сведения по мр3
- •3.8.1 Феномен мрз
- •3.8.2 Что такое формат мрз?
- •3.8.3 Качество записи мрз
- •3.8.4 Формат мрз и музыкальные компакт-диски
- •3.8.5 Работа со звукозаписями формата мрз
- •3.9 Основные понятия цифровой звукозаписи
- •3.9.1 Натуральное цифровое представление данных
- •3.9.2 Кодирование рсм
- •3.9.3 Стандартный формат оцифровки звука
- •3.9.4 Параметры дискретизации
- •3.9.5 Качество компакт-диска
- •3.9.6 Объем звукозаписей
- •3.9.7 Формат wav
- •3.10 Формат mp3
- •3.10.1 Сжатие звуковых данных
- •3.10.2 Сжатие с потерей информации
- •3.10.3 Ориентация на человека
- •3.10.4 Кратко об истории и характеристиках стандартов mpeg.
- •3.10.5 Что такое cbr и vbr?
- •3.10.6 Каковы отличия режимов cbr, vbr и abr?
- •3.10.7 Методы оценки сложности сигнала
- •3.10.8 Какие методы кодирования стерео информации используются в алгоритмах mpeg (и других)?
- •3.10.9 Какие параметры предпочтительны при кодировании mp3?
- •3.10.10 Какие альтернативные mpeg-1 Layer III (mp3) алгоритмы компрессии существуют?
- •3.11 OggVorbis
- •3.13 Flac
- •4 Сжатие видео
- •4.1 Общие положения алгоритмов сжатия изображений
- •4.1.1 Классы изображений
- •4.1.2 Классы приложений
- •4.1.3 Требования приложений к алгоритмам компрессии
- •4.1.4 Критерии сравнения алгоритмов
- •4.2 Алгоритмы сжатия
- •Gif (CompuServe Graphics Interchange Format)
- •4.3 Вейвлет-преобразования
- •4.3.1 Вейвлеты, вейвлет-преобразования, виды и свойства Вейвлет анализ и прямое вейвлет-преобразование
- •Непрерывное прямое и обратное вейвлет-преобразования
- •Ортогональные вейвлеты
- •Дискретное вейвлет-преобразование непрерывных сигналов
- •Кратномасштабный анализ
- •Пакетные вейвлеты.
- •4.3.2 Примеры применения вейвлетов Очистка сигнала от шума
- •Очистка сигнала от шумов на основе вейвлет-преобразований.
- •4.4 Формат сжатия изображений jpeg
- •2) Дискретизация
- •3) Сдвиг Уровня
- •4) 8X8 Дискретное Косинусоидальное Преобразование (dct)
- •5) Зигзагообразная перестановка 64 dct коэффициентов
- •6) Квантование
- •7) RunLength кодирование нулей (rlc)
- •8) Конечный шаг - кодирование Хаффмана
- •4.5 Jpeg2000
- •4.5.1 Общая характеристика стандарта и основные принципы сжатия
- •4.5.2 Информационные потери в jpeg2000 на разных этапах обработки
- •4.5.3 Практическая реализация
- •4.5.4 Специализированные конверторы и просмотрщики
- •4.5.5 Основные задачи для развития и усовершенствования стандарта jpeg2000
- •4.6 Видеостандарт mpeg
- •4.6.1 Общее описание
- •4.6.2 Предварительная обработка
- •4.6.3 Преобразование макроблоков I-изображений
- •4.6.4 Преобразование макроблоков р-изображений
- •4.6.5 Преобразование макроблоков в-изображений
- •4.6.6 Разделы макроблоков
- •4.7 Mpeg-1
- •Параметры mpeg-1
- •4.8 Mpeg-2
- •4.8.1 Стандарт кодирования mpeg-2
- •4.8.2 Компрессия видеоданных
- •4.8.3 Кодируемые кадры
- •4.8.4 Компенсация движения
- •4.8.5 Дискретно-косинусное преобразование
- •4.8.6 Профессиональный профиль стандарта mpeg-2
- •4.9.11 Плюсы и минусы mpeg-4
- •4.10 Стандарт hdtv
6.3 Интегрирующий рекурсивный фильтр.
Реакция рекурсивного фильтра на сигнал с учетом "памяти" исключает возможность создания фильтров с четным импульсным откликом, и частотные характеристики рекурсивных фильтров всегда являются комплексными. Проектирование рекурсивных частотных фильтров с заданными частотными характеристиками осуществляется через z-область.
Синтез рекурсивных фильтров непосредственно в z-области возможен только для фильтров простого типа (режекторных и селективных) с ограниченным количеством полюсов и нулей (особых точек). В общем случае, процесс проектирования рекурсивного частотного фильтра обычно заключается в задании необходимой передаточной характеристики фильтра в частотной области и ее аппроксимации с определенной точностью какой-либо непрерывной передаточной функцией, с последующим z-преобразованием для перехода в z-область. Первые две операции хорошо отработаны в теории аналоговой фильтрации сигналов, что позволяет использовать для проектирования цифровых фильтров большой справочный материал по аналоговым фильтрам. Последняя операция является специфичной для цифровых фильтров.
Для алгебраического преобразования непрерывной передаточной функции в многочлен по z используется билинейное преобразование, известное в теории комплексных переменных под названием дробно-линейного преобразования.
1.6.1 Принципы рекурсивной фильтрации
Конструкция РЦФ отображается в z-образе передаточной функции фильтра в виде отношения двух многочленов:
H(z) = H0+H1z+H2z2+...= B(z)/[1+A(z)], (6.1.1)
где: B(z) = B0+B1z+B2z2+ ... +BNzN, A(z) = A1z+A2z2+ ... +AMzM.
Естественно, что переход на РЦФ имеет смысл только в том случае, если степень многочленов A(z) и B(z) во много раз меньше степени многочлена H(z) прямого z-преобразования импульсной реакции фильтра. При z-образе входных данных Х(z), на выходе РЦФ имеем:
Y(z) = H(z)Х(z) = X(z)B(z)/[1+A(z)],
Y(z)[1+A(z)] = Y(z)+Y(z)A(z) = X(z)B(z),
Y(z) = X(z)B(z)-Y(z)A(z). (6.1.2)
При обратном z-преобразовании выражения (6.1.2) получаем уравнение рекурсивной цифровой фильтрации:
yk
=
bn
xk-n
–![]() am
yk-m.
(6.1.3)
am
yk-m.
(6.1.3)
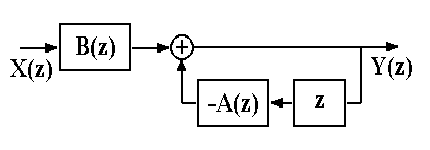 Рис.
6.1.1. Схема РЦФ.
Рис.
6.1.1. Схема РЦФ.
Как следует из выражения (6.1.3), при вычислении значения уk текущей точки используются предыдущие вычисленные значения уk-m, (m>0), что и определяет принцип рекурсии - фильтрации с обратной связью. Другой особенностью РЦФ является их односторонность и физическая реализуемость в реальном масштабе времени. При машинной обработке данных многочлен B(z) передаточной функции фильтра может реализоваться и в двухстороннем варианте.
Одно из важнейших свойств рекурсивных фильтров - возможность получения узких переходных зон при конструировании частотных фильтров, так как функция H(z) фильтра может резко изменяться при приближении к нулю многочлена в знаменателе (6.1.1).
Рекурсивная фильтрация требует более высокой точности вычислений по сравнению с нерекурсивной, т.к. использование предыдущих выходных отсчетов для текущих вычислений может приводить к накапливанию ошибок.
Практическая реализация РЦФ осуществляется в двух вариантах.
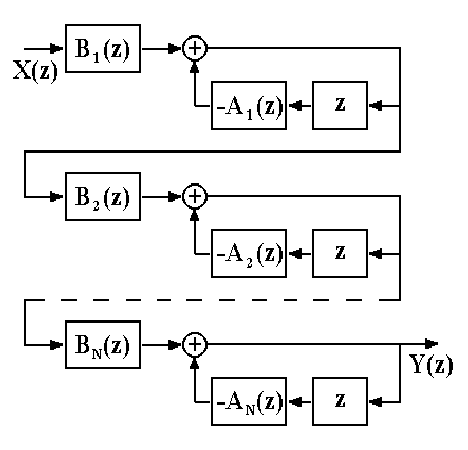
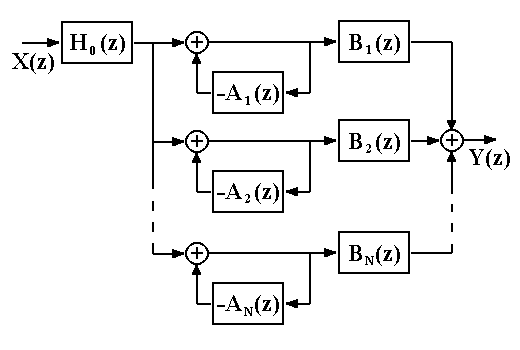
Рис. 6.1.2. Каскадная форма. Рис. 6.1.3. Параллельная форма.
Каскадная форма. Находятся корни многочленов А(z),B(z) и производится разложение H(z):
H(z)
=
![]() ,
(6.1.4)
,
(6.1.4)
где G - масштабный множитель. Это позволяет применять каскадное построение фильтров, показанное на рис. 6.1.2, в котором:
H(z) = G H1(z) H2(z) ..... HN(z),
Hn(z) = Bn(z)/An(z).
Функции Аn(z) и Bn(z) обычно представляются в виде биквадратных блоков (фильтров второго порядка):
Bn(z) = bn.0 + bn.1 z + bn.2 z2,
An(z) = 1 + an.1 z + an.2 z2.
Параллельная форма. Функция H(z) разлагается на элементарные дроби:
H(z) = Ho(z) Bn(z) / [1+An(z)],
что дает параллельную форму фильтра, показанную на рис. 6.1.3. Параллельная конструкция фильтра применяется много реже каскадной, хотя это может объясняться и тем, что в аналоговых фильтрах, исторически предшествовавших цифровым фильтрам, теоретическая база анализа и синтеза каскадных рекурсивных фильтров получила весьма детальное развитие.
Устранение сдвига фазы. Рекурсивные фильтры являются фазо- сдвигающими фильтрами. Если требуется обеспечить нулевой фазовый сдвиг, то операция фильтрации производится дважды, в прямом и обратном направлении числовой последовательности массива данных, при этом амплитудно-частотная характеристика (АЧХ) фильтрации будет равна |H()|2 фильтра, что необходимо учитывать при конструировании фильтра.
