Задача 4

В тире имеется 5 различных по точности боя винтовок. Вероятность попадания в мишень для данного стрелка соответственно равна 0.5, 0.55, 0.7, 0.75 и P. Чему равна вероятность попадания в мишень, если стрелок делает один выстрел из случайно выбранной винтовки? Попадание произошло. Чему равна вероятность того; что была выбрана первая винтовка?

Исходные данные: P = 0.6.

Решение:

Рассмотрим событие, когда стрелок совершил попадание из случайно выбранной винтовки. Обозначим его A. Выбор любой из винтовок равновозможен, поэтому вероятность выбора каждой из них равна 0.2.

По формуле полной вероятности вероятность рассматриваемого события равна:

Рассмотрим событие, когда попадание произошло. Это событие обозначено у нас A. Условие, что была выбрана именно первая винтовка, является для этого события гипотезой. Обозначим ее . Вероятность выбора первой винтовки равна 0.2. Но поскольку было произведено попадание в мишень, событие случилось, а вероятность попадания из первой винтовки самая низкая, то и вероятность выбора первой винтовки в этом случае очевидно должна быть меньше 0.2.

Фактически задача сводится к тому, чтобы найти условную вероятность P( B₁| A ) для гипотезы при свершении события A. Для этого воспользуемся формулой Байеса:

Для сравнения для четвертой (самой пристреленной) винтовки условная вероятность будет равна:

Ответ: ,

Задача 5

Вероятность того, что баскетболист при броске попадет в корзину, равна p. Определить вероятность того что, сделав n бросков, он m раз попадет.

Исходные данные: n = 9, m = 4, p = 0.1.

Решение:

Данная задача являет собой пример о повторных независимых испытаниях. Для расчета искомой вероятности в данном случае лучше использовать формулу Бернулли:

,

где – вероятность промаха в каждом броске,

Ответ:

Задача 6

Вероятность появления бракованных деталей при их массовом производстве равна p. Определить вероятность того, что в партии из N деталей будет: ровно 3 бракованных, не более 3-х бракованных.

Исходные данные: N = 2000, p = 0.001.

Решение:

Для решения таких задач используют приближенные формулы. Мы воспользуемся формулой Пуассона (так как p меньше 0.1):

, где для нашего случая ,

Соответственно вероятность того, что в данной партии будет ровно три бракованные детали, будет равна:

.

Найдем вероятность того, что в данной партии будет не более трех бракованных деталей. По теореме сложения несовместных событий будем иметь:

.

Ответ: ,

Задача 7

В жилом доме имеется n ламп, вероятность включения каждой из них в вечернее время равна 0.5. Найти вероятность того, что число одновременно включенных ламп будет заключено между и .

Исходные данные: n =6400 , = 3200, = 3240.

Решение:

Поскольку n существенно больше 15 для решения этой задачи можно использовать интегральную предельную теорему Лапласа, описываемую приближенной формулой:

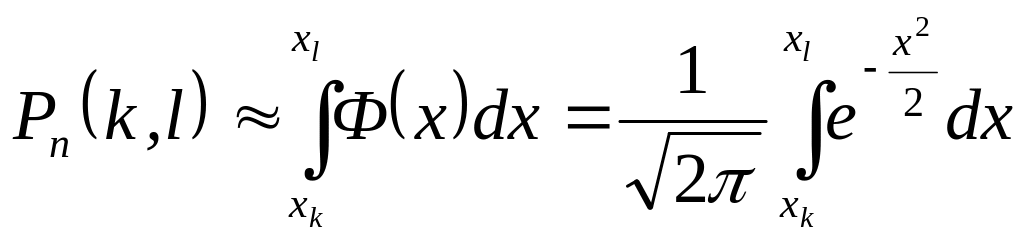, где ,

Для практического применения Лаплас ввел функцию , называемую функцией Лапласа или интегралом вероятностей.

После подстановки интегральная формула Лапласа примет вид:

, где , , , ,

– вероятность не включения для каждой из ламп.

Функция Лапласа вычисляется с помощью таблиц.

Таким образом, искомая вероятность будет равна:

Подставляя в полученную формулу значения функции Лапласа, получим искомую вероятность того, что число одновременно включенных ламп будет заключено в указанном интервале:

0.1915 – 0 0.1915

Ответ: 0.1915