
Тема: Работа. Энергия
1 .Тело
движется под действием силы, зависимость
проекции которой от координаты
представлена на графике. Работа силы
(в
.Тело
движется под действием силы, зависимость
проекции которой от координаты
представлена на графике. Работа силы
(в
![]() )
на пути 4 м равна …
)
на пути 4 м равна …
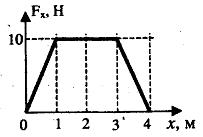 Решение:
Работа
переменной силы на участке
Решение:
Работа
переменной силы на участке
![]() определяется
как:
определяется
как: ,
т.е. численно равна площади трапеции
,
т.е. численно равна площади трапеции
![]()
2. На рисунке показан вектор силы, действующей на частицу: Работа, совершенная этой силой при перемещении частицы из начала координат в точку с координатами (5; 2), равна _____ .
Решение:
По определению
![]() .
С учетом того, что
.
С учетом того, что
![]() (см.
рис.),
(см.
рис.),
![]()
3. Частица совершила перемещение по
некоторой траектории из точки M (3, 2)
в точку N (2, –3). При этом на нее
действовала сила
![]() (координаты
точек и сила
(координаты
точек и сила
![]() заданы
в единицах СИ). Работа, совершенная силой
,
равна …
заданы
в единицах СИ). Работа, совершенная силой
,
равна …
Решение: По определению
.
С учетом того, что
![]()
![]()
4. Материальная точка массой
![]() начинает
двигаться под действием силы
начинает
двигаться под действием силы
![]() (Н)
. Если зависимость радиуса-вектора
материальной точки от времени имеет
вид
(Н)
. Если зависимость радиуса-вектора
материальной точки от времени имеет
вид
![]() (м),
то мощность (Вт), развиваемая силой
в момент времени
(м),
то мощность (Вт), развиваемая силой
в момент времени
![]() равна …
равна …
Решение:
Мгновенная мощность:![]() ,
где
,
где
![]() скорость
материальной точки, равная:
скорость
материальной точки, равная:
![]() .
Следовательно,
.
Следовательно,
![]() .
В момент
.
В момент
![]() 1с
1с
![]() 12
Вт.
12
Вт.
5. Для того чтобы раскрутить стержень
массы
![]() и
длины
и
длины
![]() (см.
рисунок) вокруг вертикальной оси,
проходящей перпендикулярно стержню
через его середину, до угловой скорости
(см.
рисунок) вокруг вертикальной оси,
проходящей перпендикулярно стержню
через его середину, до угловой скорости
![]() ,
необходимо совершить работу
,
необходимо совершить работу
![]() .
Для того чтобы раскрутить до той же
угловой скорости стержень массы
.
Для того чтобы раскрутить до той же
угловой скорости стержень массы
![]() и
длины
и
длины
![]() ,
необходимо совершить работу в _____
раз(-а) бόльшую, чем
.
,
необходимо совершить работу в _____
раз(-а) бόльшую, чем
.
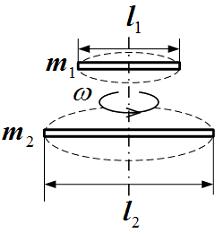
Решение:
Совершенная работа равна
кинетической энергии вращательного
движения стержня
![]() ,
где момент инерции стержня
,
где момент инерции стержня
![]() пропорционален
массе и квадрату длины,
пропорционален
массе и квадрату длины,
![]() (момент
инерции стержня массы
(момент
инерции стержня массы
![]() и
длины
и
длины
![]() относительно
оси, проходящей перпендикулярно ему
через середину стержня, равен
относительно
оси, проходящей перпендикулярно ему
через середину стержня, равен ![]() ).
Следовательно, работа по раскручиванию
до такой же угловой скорости
стержня
вдвое бόльшей массы и в два раза длиннее
будет в 8 раз больше:
).
Следовательно, работа по раскручиванию
до такой же угловой скорости
стержня
вдвое бόльшей массы и в два раза длиннее
будет в 8 раз больше:
![]() .
.
Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии r1 друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посередине между шариками. Стержень раскрутили из состояния покоя до угловой скорости
 ,
при этом была совершена работа А1.
Шарики раздвинули симметрично на
расстояние r2
= 2r1
и раскрутили до той же угловой скорости.
При этом была совершена работа …
,
при этом была совершена работа А1.
Шарики раздвинули симметрично на
расстояние r2
= 2r1
и раскрутили до той же угловой скорости.
При этом была совершена работа …
![]() ,
,
![]() ,
,
![]() ,
,
![]()

Решение:
Так как
![]() ,
т.к.
,
т.к.
![]() (
из состояния покоя),
(
из состояния покоя),
![]()
Следовательно
![]() ,
т.е.
.
,
т.е.
.
7 .
На концах невесомого стержня длины l
закреплены два маленьких массивных
шарика. Стержень может вращаться в
горизонтальной плоскости вокруг
вертикальной оси, проходящей через
середину стержня. Стержень раскрутили
до угловой скорости
.
На концах невесомого стержня длины l
закреплены два маленьких массивных
шарика. Стержень может вращаться в
горизонтальной плоскости вокруг
вертикальной оси, проходящей через
середину стержня. Стержень раскрутили
до угловой скорости
![]() .
Под действием трения стержень остановился,
при этом выделилось 4 Дж теплоты.
Если стержень раскрутить до
угловой скорости
.
Под действием трения стержень остановился,
при этом выделилось 4 Дж теплоты.
Если стержень раскрутить до
угловой скорости![]() ,
то при остановке стержня выделится
количество теплоты (в Дж), равное …
,
то при остановке стержня выделится
количество теплоты (в Дж), равное …
Решение:
Согласно закону сохранения
энергии количество выделившейся теплоты
равно убыли полной механической энергии,
в данном случае – убыли кинетической
энергии вращения:
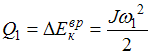 .
Отсюда следует, что при уменьшении
угловой скорости в 2 раза количество
выделившейся теплоты уменьшится в 4
раза, то есть
.
Отсюда следует, что при уменьшении
угловой скорости в 2 раза количество
выделившейся теплоты уменьшится в 4
раза, то есть
![]()
8. Потенциальная энергия частицы
задается функцией
![]() .
.
![]() -компонента
(в Н) вектора силы, действующей на
частицу в точке А (3, 1, 2),
равна …(Функция
-компонента
(в Н) вектора силы, действующей на
частицу в точке А (3, 1, 2),
равна …(Функция
![]() и
координаты точки А заданы в единицах
СИ.)
и
координаты точки А заданы в единицах
СИ.)
Решение:
Связь между потенциальной
энергией частицы и соответствующей ей
потенциальной силой имеет вид
![]() ,
или
,
или
![]() ,
,
 ,
,
![]() .
Таким образом,
.
Таким образом,
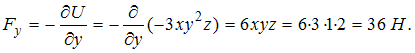
9. Потенциальная энергия частицы в
некотором силовом поле задана функцией
![]() Работа
потенциальной силы (в Дж) по перемещению
частицы из точки В (1, 1, 1) в точку
С (2, 2, 2) равна … (Функция
и
координаты точек заданы в единицах СИ.)
Работа
потенциальной силы (в Дж) по перемещению
частицы из точки В (1, 1, 1) в точку
С (2, 2, 2) равна … (Функция
и
координаты точек заданы в единицах СИ.)
Решение:
Работа потенциальной
силой совершается за счет убыли
потенциальной энергии частицы:
![]() .
Тогда
.
Тогда
![]()
10. Потенциальная энергия частицы
задается функцией
![]()
![]() -компонента
(в Н) вектора силы, действующей на
частицу в точке А (1, 2, 3), равна …
(Функция
и
координаты точки А и заданы в единицах
СИ.)
-компонента
(в Н) вектора силы, действующей на
частицу в точке А (1, 2, 3), равна …
(Функция
и
координаты точки А и заданы в единицах
СИ.)
Решение:
Связь между потенциальной
энергией частицы и соответствующей ей
потенциальной силой имеет вид:
,
или
,
,
.
Таким образом,
![]()
