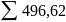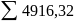- •III.Раздел – вариант №12
- •1.2. Ранжированный первоначальный ряд в порядке возрастания значений признака
- •1.3. Дискретный вариационный ряд
- •1.7. Для дискретного вариационного ряда вычислить показатели вариации:
- •1.8. . Для интервального вариационного ряда вычислить показатели вариации:
- •Раздел II. Статистические группировки
- •2.1. Имеются данные о показателях деятельности 30-ти строительных предприятий.
- •2.2.2. Провести аналитическую группировку рассматриваемого признака.
- •Вспомогательная таблица группировки
- •2.2.3. Рассчитаем величины средней из внутригрупповых, межгрупповой и общей дисперсии.
- •Раздел III. Ряды динамики
1.7. Для дискретного вариационного ряда вычислить показатели вариации:
а) среднее линейное отклонение
Таблица 1.6
Вспомогательная таблица для расчета показателей вариации
xi |
f |
хi*f |
|xi- |
|xi- |*f |
|xi- |2 |
|xi- |2*f |
1 |
14 |
14 |
7,17 |
100,38 |
51,41 |
719,74 |
2 |
5 |
10 |
6,17 |
30,85 |
38,07 |
190,35 |
3 |
6 |
18 |
5,17 |
31,02 |
26,73 |
160,38 |
4 |
9 |
36 |
4,17 |
37,53 |
17,39 |
156,51 |
5 |
8 |
40 |
3,17 |
25,36 |
10,05 |
80,4 |
6 |
5 |
30 |
2,17 |
10,85 |
4,71 |
23,55 |
7 |
9 |
63 |
1,17 |
10,53 |
1,37 |
12,33 |
8 |
8 |
64 |
0,17 |
1,36 |
0,03 |
0,24 |
9 |
11 |
99 |
0,83 |
9,13 |
0,67 |
7,58 |
10 |
2 |
20 |
1,83 |
3,66 |
3,35 |
6,67 |
11 |
4 |
44 |
2,83 |
11,32 |
8 |
32 |
12 |
1 |
12 |
3,83 |
3,83 |
14,67 |
14,67 |
13 |
3 |
39 |
4,83 |
14,49 |
23,33 |
69,99 |
14 |
2 |
28 |
5,83 |
11,66 |
33,99 |
67,98 |
16 |
2 |
32 |
7,83 |
15,66 |
61,3 |
122,62 |
18 |
2 |
36 |
9,83 |
19,66 |
96,63 |
193,26 |
19 |
2 |
38 |
10,83 |
21,66 |
117,29 |
234,58 |
21 |
1 |
21 |
12,83 |
12,83 |
164,1 |
164,1 |
22 |
1 |
22 |
13,83 |
13,83 |
191,27 |
191,27 |
26 |
1 |
26 |
17,83 |
17,83 |
317,91 |
317,91 |
28 |
1 |
28 |
19,83 |
19,83 |
393,23 |
393,23 |
31 |
2 |
62 |
22,83 |
45,66 |
521,21 |
1042,42 |
35 |
1 |
35 |
26,83 |
26,83 |
719,85 |
719,85 |
|
|
|
|
|
|
|
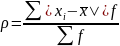
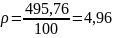
б) дисперсия
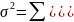
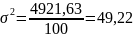
в) среднее квадратическое отклонение
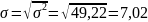
г) размах вариации
R=хmax-хmin
R=35-1=34
д) коэффициент вариации
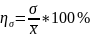

1.8. . Для интервального вариационного ряда вычислить показатели вариации:
Таблица 1.7
Вспомогательная таблица для расчета показателей вариации
Интервал по х |
Центр интервала хцi |
f |
хцi*fi |
|хцi- |
|хцi- *f |
(хцi- |
(хцi- 2*f |
1 – 6 |
3 |
47 |
141 |
5,28 |
248,16 |
27,88 |
1310,36 |
6 – 12 |
9 |
35 |
315 |
0,72 |
25,2 |
0,52 |
18,2 |
12 – 18 |
15 |
9 |
135 |
6,72 |
60,48 |
45,16 |
406,44 |
18 – 24 |
21 |
4 |
84 |
12,72 |
50,88 |
161,8 |
647,2 |
24 – 30 |
27 |
2 |
54 |
18,72 |
37,44 |
350,44 |
700,88 |
30 – 36 |
33 |
3 |
99 |
24,72 |
74,16 |
611,08 |
1833,24 |
|
|
|
|
|
|
|
|
а)среднее линейное отклонение
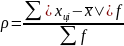
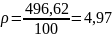
б) дисперсия
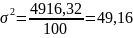
в) среднее квадратическое отклонение
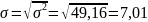
г) размах вариации
R=хmax-хmin
R=33-3=30
д) коэффициент вариации
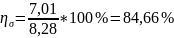
1.9. Изобразить вариационные ряды графически в виде:
а)
гистограммы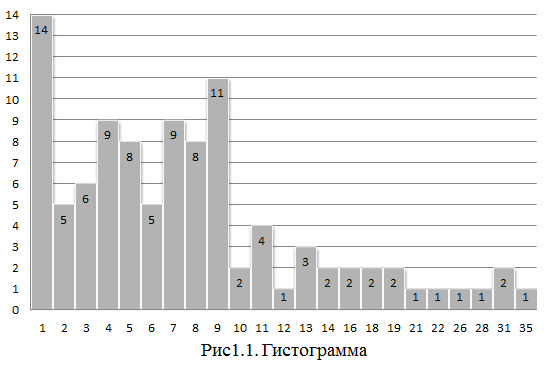
б) полигона
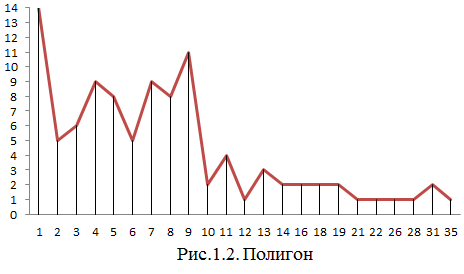
в) кумуляты
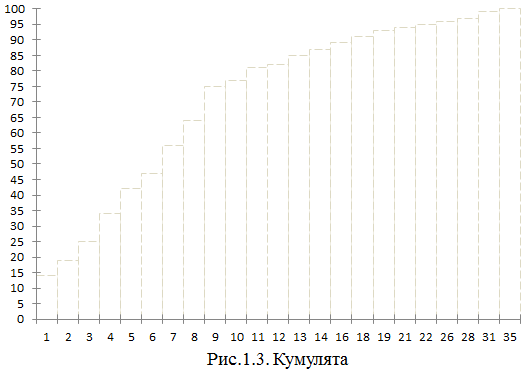
г) огивы
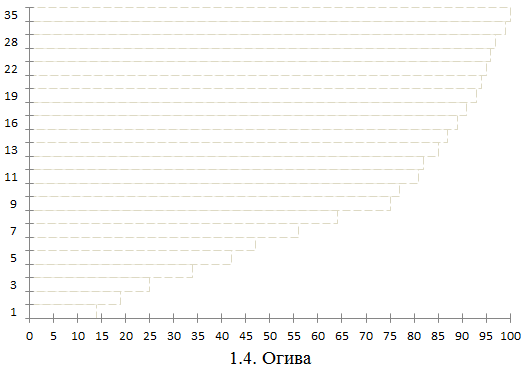
1.9. Анализ полученных результатов
Таблица 1.8
№ |
Показатели |
Дискретный ряд |
Интервальный ряд |
1 |
Средняя арифметическая |
8,17 |
8,28 |
2 |
Мода |
1 |
6 |
3 |
Медиана |
1 |
8 |
4 |
Среднее линейное отклонение |
4,96 |
4,97 |
5 |
Дисперсия |
49,22 |
49,16 |
6 |
Среднее квадратическое отклонение |
7,02 |
7,01 |
7 |
Коэффициент вариации |
85,92 |
84,66 |
8 |
Размах вариации |
34 |
30 |

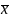 |
|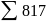

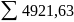
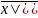
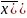 2
2