1.2. Относительные показатели

Темп роста (%) исчисляется для оценки интенсивности, т.е. относительного изменения уровня динамического ряда за какой-либо период времени (см. также Коэффициент роста):

– цепной, %,

; (4)

– базисный,%,

. (5)

Коэффициент роста показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы) – всегда положителен (см. также Темп роста):

– цепной

(т.е. ), (6)

заметим, произведение последовательных цепных коэффициентов равно базисному коэффициенту за весь период:

; (а)

– базисный

(т.е. ), (7)

заметим, частное от деления последующего базисного коэффициента роста на предыдущий равно соответствующему цепному коэффициента роста.

Темп прироста (%) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения, и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения (темп прироста может быть >0, <0, =0) (заметим, темпы прироста нельзя ни суммировать, ни перемножать) (см. также Коэффициент прироста):

; (8)

– цепной, %, (см. также Темп прироста)

; (9)

– базисный, %, (см. также Темп прироста)

. (10)

Коэффициент прироста – темп прироста, выраженный в долях единицы (можно выразить, в частности, через коэффициент роста:) (см. также Темп прироста).

= или (11)

Относительное ускорение, %, есть отношение абсолютного ускорения к абсолютному приросту , т.е. относительное ускорение есть темп прироста абсолютного прироста (вычисляется лишь в том случае, если абсолютный прирост, принятый за базу сравнения, >0).

1.3. Обобщающие показатели

Обобщающие показатели применяются как обобщающие характеристики динамики исследуемого явления и обобщают хронологическую вариацию. При вычислении обобщающих показателей применяются формулы средней хронологической.

Средняя хронологическая есть средняя, исчисленная из значений, изменяющихся во времени, т.е. из уровней ряда динамики. В хронологической средней отражается совокупность тех условий, в которых развивалось изучаемое явление в данном промежутке времени. Способы расчета средней хронологической зависят от характера ряда динамики, т.е. от его классификационных признаков. Формулы средних хронологических для исчисления обобщающих показателей, приведены при раскрытии понятий соответствующих показателей в дальнейшем изложении.

Средний абсолютный прирост (обобщающий показатель скорости изменения уровней во времени) дает возможность установить, насколько в среднем за единицу времени должен увеличиться уровень ряда (в абсолютном выражении), чтобы, отправляясь от начального уровня за данное число периодов (напр,. лет), достичь конечного уровня:

а) по цепным данным , (12)

где n – число цепных абсолютных приростов ;

б) по базисным (накопленным) данным , (13)

где m – число уровней ряда динамики, включая базисный.

Средний темп роста (сводная обобщающая характеристика интенсивности изменения уровней ряда динамики) показывает, во сколько раз в среднем за единицу времени изменился уровень динамического ряда, представляет собой средний коэффициент роста, выраженный в % ( ).

Средний коэффициент роста исчисляется следующим образом.

I) для равноотстоящих рядов динамики расчеты сводятся:

а) по средней геометрической – к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»):

= = (14)

где n – число цепных коэффициентов роста;

– цепные коэффициенты роста; – базисный коэффициент роста за весь период);

б) по (базисному способу) – к формуле

, (15)

где m – число уровней ряда динамики в изучаемом периоде, включая базисный.

II) для разноотстоящих (т.е. по периодам различной продолжительности) рядов динамики при расчетах пользуются средними геометрическими взвешенными:

(16)

где t– интервал, в течение которого сохраняется данный темп роста; – сумма отрезков периода).

Средний темп прироста рассчитывается на основе среднего темпа роста, вычитанием из последнего 100%:

= – 100. (17)

Средний коэффициент прироста рассчитывается на основе среднего коэффициента роста, вычитанием из последнего единицы:

= – 1. (18)

Средний уровень ряда характеризует обобщенную величину абсолютных уровней и рассчитывается по средней хронологической.

I) для интервальныx рядов динамики вычисляется по формуле средней арифметической:

а) при равных интервалах используется средняя арифметическая простая, т.е.

, (19)

где – абсолютные уровни ряда, n – число уровней ряда;

б) при неравных интервалах используется средняя арифметическая взвешенная, т.е.

, (20)

где – уровни ряда динамики, сохраняющиеся без изменения в течение соответствующих промежутков , – веса, длительность интервалов времени (напр., дней, лет) меду смежными датами;

II) для моментных рядов динамики:

а) с равнотстоящими интервалами используется формула средней хронологической моментного ряда, т.е.

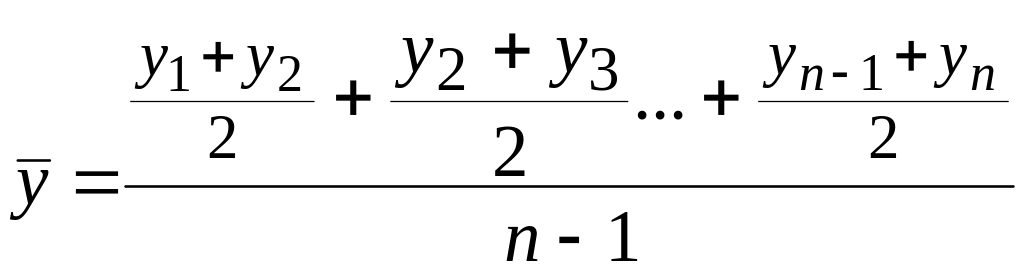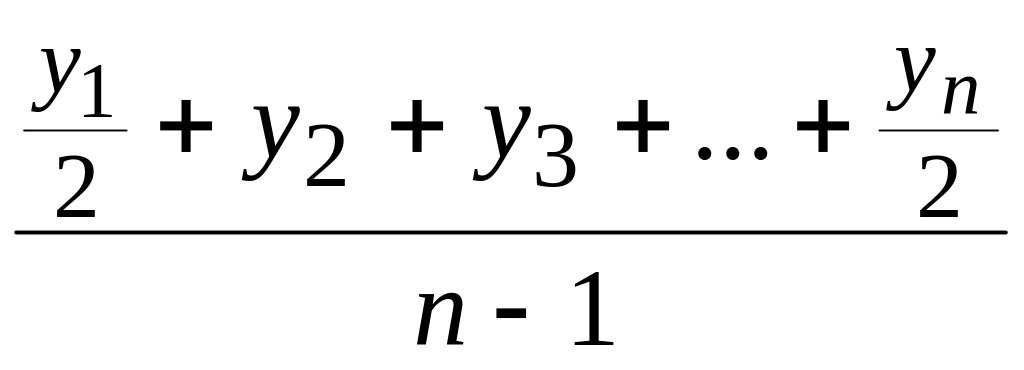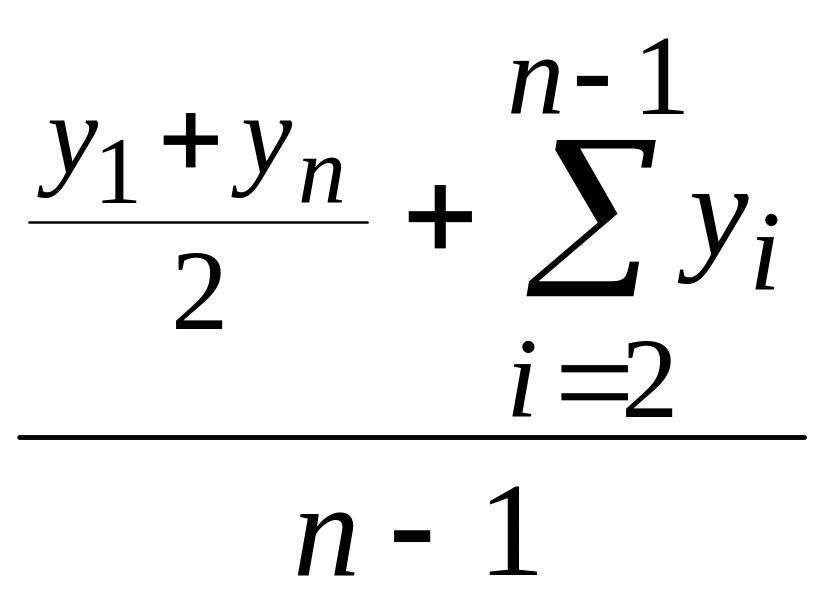= = , (21)

где – абсолютные уровни ряда, n – число уровней ряда;

б) с неравнотстоящими интервалами используется формула средней хронологической взвешенной, т.е.

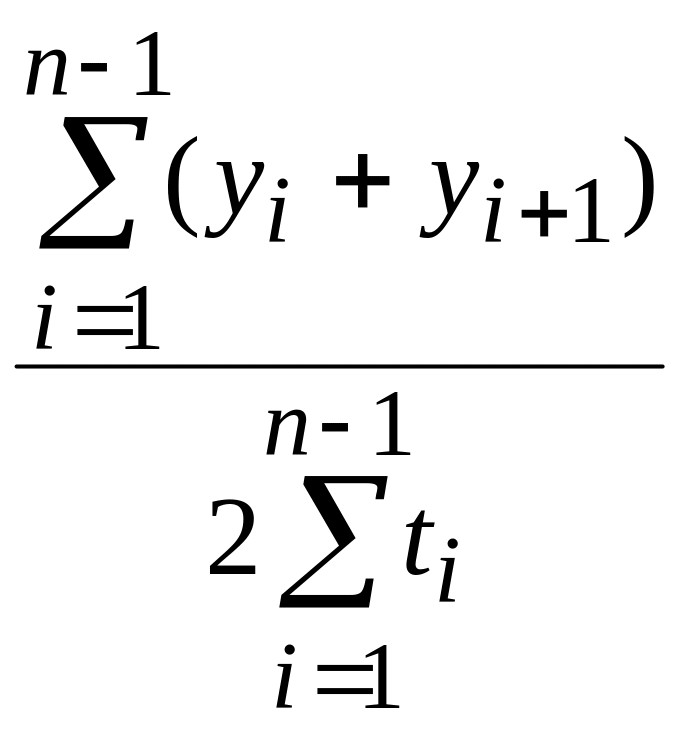= = , (22)

где – уровни ряда динамики, – интервал времени между смежными уровнями.

В качестве иллюстрации приводим анализ динамики численности работников на предприятии за 1990 – 1995 гг. (см. табл. 1). В этой таблице в столбцах соответственно представлены:

(1): i – порядковые номера индексов;

(2): – годы;

(3): – численность работников предприятия;

(4): = – абсолютный прирост цепной или первые конечные разности (i = 1, 2, 3, 4, 5), напр., 272 – 250 = 22;

(5): = – абсолютное ускорение или вторые конечные разности (i = 2, 3, 4, 5), напр., 15 – 22 = – 7;

(6): = – третьи конечные разности (i = 3, 4, 5), напр., – 4– ( – 7) = 3;

(7): = – четвертые конечные разности (i = 4, 5) напр., – 1– 3) = – 4;

(8): = – пятые конечные разности (i = 5); в данном примере = – 1 – ( –4) = 3;

(9): = – абсолютный прирост базисный (i = 1, 2, 3, 4, 5), напр., 272 –250 = 22, 287 – 250 = 37 и т.д.;

(10): = – абсолютное значение 1% (i = 2, 3, 4, 5), напр., 250 / 100 = 2.50%;

(11): – пункты роста, вычисляются следующим образом (см нижнюю строку столбца 13 табл. 1): напр., 8.8 – 0 = 8.8, 14.8 – 8.8 = 6.0, 19.2 – 14.8 = 4.4 и т.д.

(12), верхняя строка: – коэффициент роста цепной (i = 1, 2, 3, 4, 5), напр., , и т.д.; соответствующие им цепные темпы роста, %, можно определить из выражения = , т.о. = 91.1%, = 94.8% и т.д. (ввиду их очевидности, в таблице они не приведены).

(12), нижняя строка: – коэффициент роста базисный (i = 1, 2, 3, 4, 5), напр., , и т.д.; соответствующие им базисные темпы роста, %, можно определить из выражения = , т.о. = 108.8%, = 114.8% и т.д. (как и цепные темпы роста, в таблице они не приведены).

(13), верхняя строка: – 100% – темп прироста цепной, напр., 91.9 – 100 = – 8.1%, 94.8 – 100 = 5.2% и т.д.; соответствующие им цепные коэффициенты прироста, можно определить из выражения = , т.о. – 8.1/100 = – 0.0081, – 5.2/100 = – 0.0052 и т.д. (как и цепные темпы роста, в таблице они не приведены).

(13), нижняя строка: – 100% – темп прироста базисный; напр., 108.8 – 100 = 8.8%, 114.8 – 100 = 14.8% и т.д.; соответствующие им базисные коэффициенты прироста, можно определить из выражения = , т.о., 8.8/100 = 0.0088,

14.8/100 = 0.0148 и т.д. (как и цепные темпы роста, в таблице они не приведены).

(14): – относительное ускорение (i = 2, 3, 4, 5); напр. (см столбцы 5 и 4), 100 (– 7/22) = – 31/8%, 100 (– 4/15) = – 26.7% и т.д.

Таблица 1.

I	Годы		Абсолютные показатели								Относительные показатели
			=
1	2	3	4	5	6	7	8	9	10	11	12	13	14
0	1990	250	–*	–	–	–	–	–	–	–	– 1.000	– –	–
1	1991	272	22	–	–	–	–	22	2.50	– + 8.8	1.088 1.088	– 8.1 + 8.8	–
2	1992	287	15	– 7	–	–	–	37	2.72	– + 6.0	1.055 1.148	– 5.2 + 14.8	– 31.8
3	1993	298	11	– 4	3	–	–	48	2.87	– + 4.4	1.038 1.192	– 3.7 + 19.2	– 26.6
4	1994	304	6	– 5	– 1	– 4	–	54	2.98	– + 2.4	1.020 1.216	– 2.0 + 21.6	– 45.5
5	1995	303	– 1	– 7	– 2	– 1	3	53	3.04	– – 1.4	0.997 1.212	+ 0.0 + 20.2	– 116.7
											П=1.212 –
* показатели не существуют