1. Представление информации в компьютере.

Компьютер может обрабатывать только информацию, представленную в числовой форме. Вся другая информация (например, звук, изображения, показания приборов и т.д.) для обработки на компьютере должна быть преобразована в числовую форму. Например, чтобы перевести в числовую форму музыкальный звук, можно через небольшие промежутки времени измерять интенсивность звука на определенных частотах, представляя результаты каждого измерения в цифровой форме. С помощью программ для компьютера можно выполнить преобразования полученной информации, например, "наложить" друг на друга звуки от различных источников. После этого результат можно преобразовать обратно в звуковую форму.

Аналогичным образом ЭВМ обрабатывает текстовую информацию. При вводе данных в компьютер каждый символ кодируется определенным числом, а при выводе на внешние устройства (экран, печать и т.д.) для восприятия человеком по этим числам строится соответствующие изоб­ражения символов. Соответствие между набором символов и цифрами называется кодировкой символов.

Как правило, все вычисления в компьютере представляются с помощью нулей и единиц. Для запоминания кодированной информации в запоминающем устройстве компьютера отводятся определенные участки памяти, которые называются ячейками. Все ячейки одинаковы и состоят из устройств, называемых разрядами, принимающими значение 0 или 1. Число разрядов во всех ячейках одинаково. Длиной ячейки (машинного слова) называется число разрядов в ячейке. Количество информации, которое можно поместить в один разряд называется битом. Как правило, команды компьютеров работают не с отдельными битами, а с восемью битами сразу. Восемь последовательных битов составляют один байт. Более крупными единицами информации являются килобайт (сокращенно обозначаемый Кб ), равный 1024 битам, и мегабайт (сокращенно обозначаемый Мб), равный 1024 Кб.

Таким образом, вся обработка информации в компьютере (преобразование, пересылка и т.д.) осуществляется только над числовыми кодами, состоящими из нулей и единиц, т.е. компьютеры работают в двоичной системе счисления.

1.1. Системы счисления.

Необходимость выполнения арифметических действий над вводимыми в ЭВМ числами предъявляет особые требования к кодированию числовой информации. Для двоичного представления чисел в ЭВМ наиболее удобной оказалась так называемая двоичная система счисления.

В общем случае система счисления представляет собой совокупность приемов и правил для записи чисел цифровыми знакам. Способов записи чисел цифровыми знаками существует множество. Любая предназначенная для практического применения система счисления должна обеспечивать:

0. возможность представления любого числа в рассматриваемом диапазоне величин;

1. единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);

2. простоту оперирования числами.

Все системы представления чисел делят на позиционные и непозиционные.

В непозиционной системе счисления значение символа не зависит от его положения в числе. Принципы построения таких систем не сложны. Для их образования используют в основном операции сложения и вычитания. Например, система с одним символом палочкой встречалась у многих народов. Для изображения какого-то числа в этой системе нужно записать определенное множество палочек, равное данному числу. Эта система неэффективна, так как запись числа получается длинной. Другим примером непозиционной системы счисления является римская система, использующая набор следующих символов: I, V, X, L, C, D и т.д. В этой системе отсутствуют отклонения от правила независимости значения цифры от положения в числе. В числах LX и XL символ X принимает два значения: +10 и -10.

В позиционной системе счисления значение цифры определяется ее положением в числе: один и тот же знак принимает различные значения. Например, в десятичном числе 222 первая цифра с права означает две единицы, соседняя с ней - два десятка, а левая две - две сотни.

Десятичная система счисления наиболее распространена в бытовой практике. Однако своему распространению она обязана не каким-то особым преимуществом перед другими системами, а достаточно случайному обстоятельству - наличию у человека на руках десяти пальцев.

Любая позиционная система счисления характеризуется основанием. Основание (базис) естественной позиционной системы счисления - число знаков или символов, используемых для изображения цифр в данной системе. Поэтому возможно бесчисленное множество позиционных систем, так как за основание можно принять любое число, образовав новую систему.

Десятичная система счисления. В десятичной системе счисления любое целое положительное число представляется в виде суммы единиц, десятков, сотен, тысяч и т.д. Например число 547 представляется в следующем виде:

547 = 5*10² + 4*10¹ + 7*10⁰

где 5 - количество сотен, 4 - количество десятков, 7 - количество единиц. Таким образом, запись числа в виде 547 представляет собой перечисление коэффициентов в разложении этого числа по степени 10. Аналогично любое число в десятичной системе счисления записывается следующим образом:

Число 10 называется основанием десятичной системы счисления. Так как 10 единиц младшего разряда составляют одну единицу старшего разряда, то каждый из коэффициентов x_i представляет собой некоторую цифру из набора {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Этот набор цифр составляет базис десятичной системы счисления. Число цифр в базисном наборе совпадает с основанием системы счисления. Однако десятичная система не является единственной. В качестве основания системы счисления можно взять любое целое число q > 1, а для базисной системы коэффициентов x_i использовать набор из p различных цифр

x  {0,1,...,q-1}.

Таким образом, произвольное число K в системе счисления с основанием р имеет вид:

К_q = x_n*qⁿ + x_n-1*q^n-1 +... + x₁*q¹ + x₀*q⁰ + x_-1*q^-1 + x_-2*q^-2 + x_mq^-m...

Двоичная система счисления. Минимальным значением основания системы счисления p > 1 является число 2. В двоичной системе базисная система коэффициентов представляет собой набор из двух цифр x_i  {0,1}. Так, например, десятичное число 51.5 в двоичном представлении имеет следующий вид:

51.5₁₀ = 1*2⁵ + 1*2⁴ + 0*2³ + 0*2² + 1*2¹ + 1*2⁰ + 1*2^-1 = 110011.1_2.

Двоичная система получила широкое распространение с появлением ЭВМ. Как правило, все числа в компьютере представлены с помощью нулей и единиц, т.е. компьютеры работают в двоичной системе счисления, поскольку при этом их устройство получается значительно более простым. Например, для того, чтобы различать цифры в такой системе, достаточно иметь устройство, обладающее двумя устойчивыми состояниями, одно из которых соответствует единице, другое - нулю (единица -ток проходит через проводник, нуль - ток не проходит). Для сравнения аналогичная задача в десятичной системе счисления требует устройства с десятью различными устойчивыми состояниями. Другим важным достоинством двоичной системы является простота вычислений. Отметим, что выполнение арифметических действий над числами в двоичной системе счисления производится по тем же правилам, что и в десятичной системе счисления. При этом пользуются следующими правилами.

Правило сложения: Правило умножения: Правило вычитания:

0 + 0 = 0 0 * 0 = 0 0 - 0 = 0

0 + 1 = 1 0 * 1 = 0 1 - 0 = 1

1 + 0 = 1 1 * 0 = 0 1 - 1 = 0

1 + 1 = 10 1 * 1 = 1 0 - 1 = -1

Отметим недостаток, характерный для двоичной системы счисления - значительный рост числа разрядов, необходимых для записи чисел. Например двузначное десятичное число 22 в двоичной системе имеет вид 10110, т.е. для его записи в двоичной системе счисления требуется уже 5 разрядов. Вместе с тем перечисленные выше достоинства двоичной системы счисления делают этот недостаток не столь существенным.

Выше было отмечено, что большинство устройств ЭВМ работают с числами, представленными в двоичной системе счисления (т.е. в виде комбинации нулей и единиц), однако задавать исходные данные и анализировать полученные результаты вычислений удобней в десятичной системе счисления. Поэтому необходим простой способ записи десятичных чисел с помощью символов двоичной системы счисления. Такую возможность обеспечивает двоично-десятичная система счисления. В ней каждая десятичная цифра записывается двоичными знаками. Ниже приведена запись в двоично-десятичной системе счисления чисел от 0 до 9, составляющих базис десятичной системы счисления:

0 = 0000 5 = 0101

1 = 0001 6 = 0110

2 = 0010 7 = 0111

3 = 0011 8 = 1000

4 = 0100 9 = 1001

Например, десятичное число 9024.19 имеет в двоично-десятичной системе следующий вид (нули, стоящие в крайних позициях, как правило, опускают):

Следует иметь в виду тот факт, что запись числа в двоично-десятичной системе счисления не совпадает в общем случае с записью того же числа в двоичной системе. Рассмотрим набор двоичных чисел 10101

0001 0101 = 15

1 5

Такая последовательность представляет собой двоично-десятичную запись числа 15. С другой стороны, если теперь эту же последовательность интерпретировать как число, записанное в двоичной системе счисления, то получим:

1*2⁴ + 0*2³ + 1*2² + 0*2¹ + 1*2⁰ = 21.

Очевидно, что полученные результаты различны. В связи с этим достаточно широкое распространение с появлением компьютеров получили восьмеричная (основание системы р = 8) и шестнадцатеричная (основание системы р = 16) системы счисления, поскольку представление восьмеричных чисел в двоичной системе счисления тождественно совпадает с их представлением в двоично-восьмеричной системе счисления. Аналогично это правило выполняется и для шестнадцатеричной системы счисления.

Восьмеричная и шестнадцатеричная системы счисления. В случае восьмеричной системы счисления основанием системы служит число 8, а базис системы составляет набор цифр x_i  {0, 1, 2, 3, 4, 5, 6, 7}. Например:

765.4 = 7*8² + 6*8¹ + 5*8⁰ + 4*8^-1

Так как базис восьмеричной системы составляют числа от 0 до 7, то для изображения любой базисной цифры достаточно трех двоичных символов. Группы из трех разрядов для изображения восьмеричных чисел принято называть триадами.

Выпишем изображение базисных цифр в двоично-восьмеричной системе:

0 = 000 4 = 100

1 = 001 5 = 101

2 = 010 6 = 110

3 = 011 7 = 111

Например:

724₈ = 111 010 100

7 2 4

При записи чисел в шестнадцатеричной системе счисления необходимо использовать 16 цифр, составляющих базис системы, однако только 10 цифр из шестнадцати имеют общепризнанное обозначение 0 - 9. Поэтому для записи остальных базисных чисел (10,11,12,13,14,15) обычно используют символы A, B, C, D, E, F.

Базис шестнадцатеричной системы составляет набор x_i  {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F} поэтому для изображения любой базисной цифры достаточно четырех двоичных символов.

Изображение базисных цифр в двоично-шестнадцатеричной системе выглядит следующим образом:

0 = 0000 4 = 0100 8 = 1000 C = 1100

1 = 0001 5 = 0101 9 = 1001 D = 1101

2 = 0010 6 = 0110 A = 1010 E = 1110

3 = 0011 7 = 0111 B = 1011 F = 1111

Например:

A792₁₆ = 1010 0111 1001 0010

A 7 9 2

Арифметические операции над числами в восьмеричной и шестнадцатеричной системе счисления, как, впрочем, и в любой другой системе, выполняются аналогично соответствующим операциям в рассмотренной выше двоичной системе, только в каждом случае используется своя таблица сложения и умножения.

Для записи одного и того же значения в различных системах счисления требуется разное число позиций или разрядов. например 961₀=140₈=1100000₂.

Чем меньше основание системы, тем больше длина числа (длина разрядной сетки).

Если длина разрядной сетки задана, то это ограничивает максимальное по абсолютному значению число, которое может быть записано.

Пусть длина разрядной сетки равна любому положительному числу, например, N. Тогда

К_qmax=q^N-1 , где q - основание системы счисления.

Однако, если задано максимальное абсолютное значение числа, то длина разрядной сетки

N=log_q(K_qmax+1). (1)

Интервал числовой оси, заключенный между максимальным и минимальным числами, называют диапазоном представления (ДП) чисел в данной системе счисления для заданного ограничения на длину разрядной сетки:

-K_qmax  ДП  K_qmax.

В ЭВМ длина обрабатываемых чисел обычно ограничена значениями: 1 байт (8 разрядов), 2 байт (16 разрядов), 4 байт (32 разряда), 8 байт (64 разряда). Соответственно ограничены и значения записываемых с использованием указанной длины разрядной сетки целых положительных чисел. Так, максимальное целое положительное число, которое может быть записано с использованием 16 двоичных разрядов, равно 2¹⁶-1=65535.

Произведение основания системы на длину разрядной сетки, выбранной для записи чисел в этой системе, называют показателем экономичности системы:

C=qN. (2)

Подставив в (2) значение N выраженное в (1), получим:

С_q=qlog_q(A_q+1).

Использование двоичной системы счисления для ЭВМ связано с преодолением дополнительных трудностей, вызванных необходимостью перевода вводимых в ЭВМ чисел в двоичную систему счисления и обратного преобразования числовых данных при выводе из ЭВМ. Эти преобразования осуществляются автоматически с использованием специально разработанных методов. В информатике и вычислительной технике разработано множество других методов перевода чисел из одной системы счисления в другую. Приведем пример одного из самых простых методов - метода перевода целых чисел и целых частей неправильных дробей, базирующегося на делении переводимого числа на основание новой системы счисления. Целое число К в системе с основанием q записывается в виде

K_q=x_n-1q^n-1+x_n-2q^n-2+...+x₁q¹+x₀q⁰.

Переписав это выражение по схеме Горнера, получим

K_q=(...(((x_n-1q+x_n-2)q+x_n-3)q...+x₁)q+x₀). (3)

Если правую часть выражения (3) разделить на величину основания q, то получим целую часть (...(x_n-1q+x_n-2)q+...+x₁) и остаток x_0. Разделив полученную часть на q, найдем второй остаток x₁. Повторяя процесс деления n раз, получим последнее частное xn-1, которое в соответствии с (3) является старшей цифрой n-разрядного числа, представленного в системе с основанием q. При переводе все арифметические действия должны вычисляться по правилам системы счисления первоначального представления числа K (c исходным основанием).

Пример 1. Перевести десятичное число 15 в двоичную систему счисления.

Ответ: x₄x₃x₂x₁x₀=10001_2.

Для перевода правильных дробей в систему с основанием q используют метод, базирующийся на умножении переводимой правильной дроби на основание q новой системы счисления. Правильная дробь может быть записана в виде

K_q=x_-1q^-1+x_-2q^-2+...+x_-mq^-m.

Переписав это выражение по схеме Горнера, получим:

Kq=q^-1(x_-1+q^-1(x_-2+...+q^-1(x_-(m-1)+q^-1x_-m)...). (4)

Если правую часть выражения (4) умножить на q, то найдем неправильную дробь, в целой части которой будет число x_-1. Умножив затем оставшуюся дробную часть на величину основания q, получим дробь, в целой части которой будет x_-2 и т.д. Повторяя процесс умножения m раз, найдем все m цифр дробной части числа в новой системе счисления.

Пример 2. перевести десятичную дробь 0.625 в двоичную систему счисления.

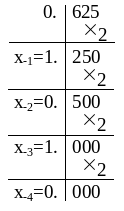
Ответ: 0,x_-1x_-2x_-3x_-4 = 0.1010_2.

В ЭВМ точность перевода (в случае бесконечного или расходящегося ряда) обычно ограничивается длиной разрядной сетки, отведенной для представления чисел.