Основні сфероїдичні функції для визначення параметрів ліній на сфероїді.
Функції
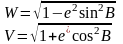(1),(2)
залежні від ексцентриситету еліпсоїда й широти, називаються основними сфероїдичними функціями. Між ними є наступний зв'язок:
(3)
Якщо врахувати формули (1), (2), то маємо наступне:
Рівняння
поверхні еліпсоїда запишемо у
векторній формі:
або, з урахуванням формул, маємо
(4)
Введемо позначення: dX, dY - диференціали дуг меридіана й паралелі; t1 (t2) - одиничний вектор, дотичний до меридіана (паралелі).
Повний диференціал вектора s:
Знайдемо частки похідні вектора s (4) :
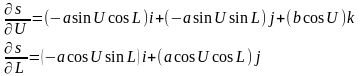(5),
(6)
Для меридіана (L=const, dL = 0) маємо:
З
уразуванням часток похідних (5):
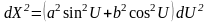(7)
Для паралелі (U= const, dU=0) маємо:
,
З
урахуванням часток похідних (6):
(8)
Користуючись раніше отриманими формулами, від наведеної широти перейдемо до геодезичної.
Тому одержуємо:
звідки,
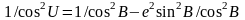
або
(9)
Аналогічно
(10)
Використовуючи співвідношення (7) — (10), одержимо шукані диференціали, виражені через геодезичні широту й довготу:
(11)
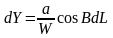(12)
Методи визначення довжин паралелей та меридіанів.
1. Визначення довжини меридіана.
Н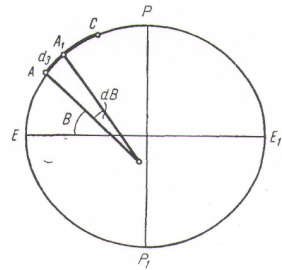
ехай
точка А (рис.1) на меридіанному еліпсі
має широту В. Візьмемо на нескінченно
малій відстані ds
від точки А точку А1, що має широту В+dB;
таким чином, різниця широт точок А та
А1, що відповідає дузі меридіана ds
буде dB.
Розглядаючи
елементарну дугу ds як дугу кола з радіусом
М, отримуємо:
ds=MdB,
або
dB=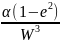
Довжина дуги меридіана між точками, що мають широти В1 та В2, буде:
Рис. 1
(1)
Таким чином, обчислення довжини меридіана зводиться до знаходження елліптичного інтеграла виду:
Для обчислення вказаного інтеграла розкладемо підінтегральну функцію 1/W3 в ряд по біному Ньютона:
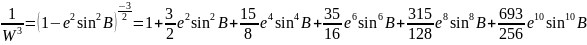+…(2)
Для спрощення подальших викладок обмежимося членами з е4. Парні степіні синусів, що входять в розклад функції 1/W3, замінимо косинусами кратних дуг згідно рівностей:
Тепер формула (2) матиме вигляд:
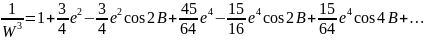
або:
(3)
Позначимо:
(4)
Отримуємо:
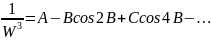(5)
Підставивши знайдене значення 1/W3 в (1), отримаємо:
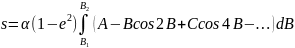(6)
Інтегруючи почленно, знаходимо:
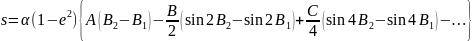(7)
Отримана формула є загальною для дуги меридіана. Але існують також часткові випадки:
При обчисленні геодезичних таблиць (наприклад, для обчислення таблиць координат Гаусса-Крюгера) довжина меридіана вираховується від екватора до точок дуги, розташованих через певні інтервали широти. Формула (7) може бути залишена без перегрупування членів і матиме вигляд:
(8)
При обробці градусних вимірів з метою виводу розмірів земного еліпсоїда (7) є незручною. В цьому випадку широти кінців виміряних меридіанних дуг, що використовуються в обробці градусних вимірів, можуть вважатися постійними; на відміну від попереднього випадку розміри еліпсоїда потребують визначення. Тому необхідно розташувати члени ряду, що виражає дугу меридіана, так, щоб навколо визначуваних величин а, е2, е4 і т.д. сгрупувати постійні члени. В результаті отримаємо:
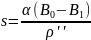
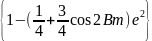(9)
Для обчислень в триангуляції, коли сторони незначні та рідко перебільшують 40-50 км, є більш зручна формула. Для цього введемо допоміжну величину:
яка
представляє собою довжину дуги кола з
радіусом, рівним радіусу кривизни
меридіана в точці з середньою широтою.
В результаті перетворень отримаємо:
(10)
2. Обчислення довжини паралелі.
Паралель на еліпсоїді обертання є колом, тому обчислення паралелі зводиться до визначення дуги кола з центральним кутом, рівним різниці довгот кінцевих точок дуги. Радіус паралелі r визначається за формулою:
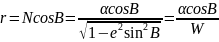(11)
Довжина паралелі s, що має широту В та різницю довгот кінцевих точок дуги l, задається формулою:
(12)
Звідси легко отримуємо різницю довгот двох точок паралелі під широтою В, розташованих на відстані s:
(13)