6. Загальна характеристика ліній на поверхнях. Поняття про кривизну ліній та геодезичну лінію.

За допомогою ліній вдається вирішувати багато наукових і інженерних завдань. У загальному випадку лінія може належати поверхні або не належати. Лінія належить поверхні, якщо всі її крапки належать цій поверхні. Лише коли лінія представлена прямою, а поверхня — площиною, то для приналежності прямої площині вистачає, аби хоча б дві крапки її належали цій поверхні.

Взагалі, поверхня може бути задана рівнянням 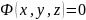або або ж в параметричному вигляді трьома рівняннями де α, β - параметри. Лінія на поверхні, заданій параметрично, задається цими ж рівняннями, якщо α и β - функції одного параметра. Лінії α=const, β=const const утворюють на поверхні мережу криволінійних координат. Квадрат диференціала ds довжини дуги лінії на поверхні можна представити у вигляді

Де 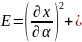; ; 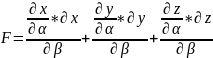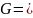коефіцієнти Гауса. Вираз Edα2+2Fdαdβ+Gdβ2 називається першою квадратичною формою поверхні.

Одним з елементів, що характеризує форму лінії (кривої), є міра її викривленості. Нехай ми маємо криву, яка не перетинає саму себе і має певну дотичну в кожній точці. Проведемо дотичні до кривої в будь-яких двох її точках А та В і позначимо через кут, утворений цими дотичними. Кср= - середня кривизна дуги АВ. Кривизною лінії в даній точці А називається границя середньої кривизни дуги АВ, коли довжина цієї дуги прагне до нуля. КA = 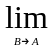Kcp=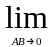 . Для довільної кривої кривизна в різних її точках буде різна.

Розглянемо будь-яку лінію L1, проведену на поверхні через її точку M1. . Проекція вектора кривизни Kv на напрям вектора в точці М1 називається нормальною кривизною лінії L1 в точці М1. Лінія на поверхні, у якої в кожній точці нормальна кривизна дорівнює нулю, називається асимптотичною лінією. Величина Kn (або нормальна кривизна лінії на поверхні) визначається по формулі . Вираз Ldα2 + 2Mdαdβ+Ndβ2 називається другою квадратичною формою поверхні.

Напрями дотичних до головних нормальних перетинів поверхні називаються головними напрямами на поверхні. Лінія на поверхні, в кожній точці якої дотична має головний напрям, називається лінією кривизни. Через кожну точку поверхні проходять дві взаємно ортогональні лінії кривизни. - середня, а K = κ1κ2 - гаусова кривизни поверхні.

У сфероїдичній геодезії точки на поверхні еліпсоїда з'єднуються геодезичними лініями, які визначаються як найкоротші відстані на даній поверхні між заданими точками. Геодезична лінія на даній поверхні — така крива, в кожній точці якої головна нормаль збігається з нормаллю до по­верхні. Вона відіграє роль прямої лінії на площини або дуги великого круга на сфері. Геодезична лінія характеризуються тим, що її геодезична кривизна дорівнює нулю у всіх її точках. Важливо зазначити, що геодезична лінія є асимптотичною тоді і лише тоді, коли вона пряма, а плоска геодезична лінія є в той же час і лінією кривизни.

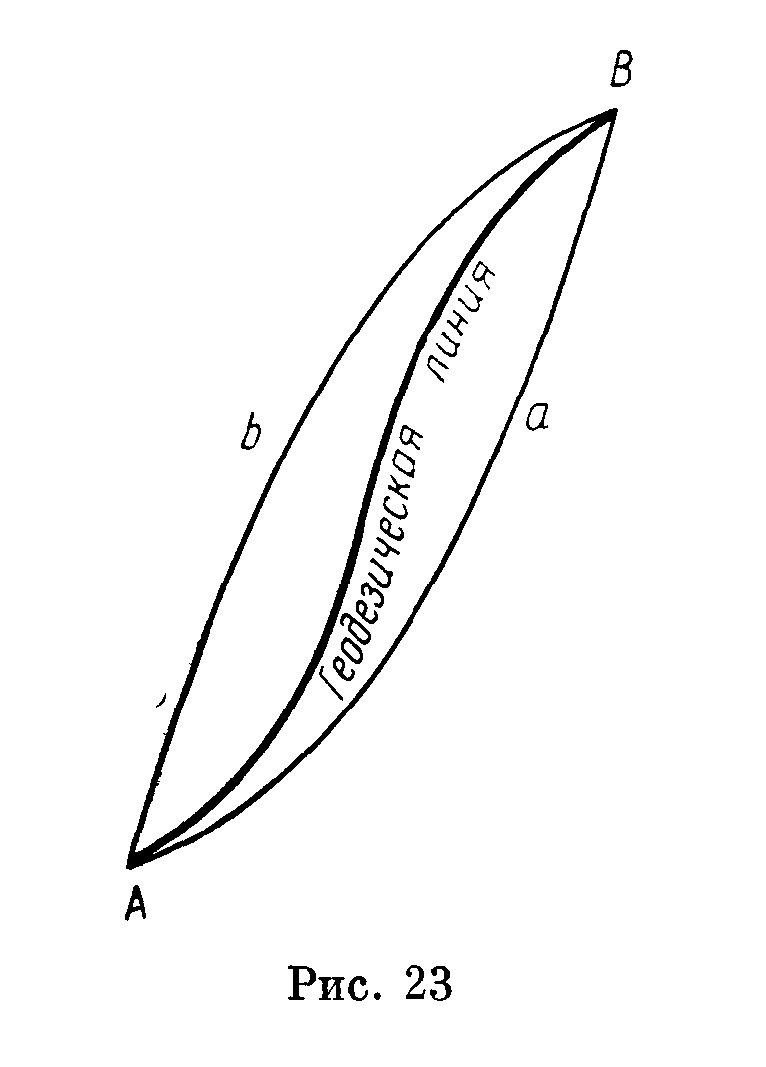
Рівняння геодезичної лінії для довільної поверх­ні має вигляд:

.

Рівняння геодезичної лінії на поверхні обертання має вигляд:

, де С - постійна інтеграції.