2.2. Определение главных центральных моментов инерции сечения

1. Определяют положение центра тяжести сечения (см. поря- -\ док решения задачи для самостоятельной работы У). ]

2. Проводят центральные оси для каждого профиля проката или простой геометрической фигуры. Эти оси называются центральными осями. Для первой фигуры проводят оси X] и y_l , для второй — х₂ и у₂ и т.д.

3. Проводят главные центральные оси. Они проходят через центр тяжести всего сечения. Одну из осей совмещают с осью симметрии (в задании все сечения имеют такую ось), а вторую i проводят через центр тяжести сечения перпендикулярно первой. Вертикальная ось обозначается v, а горизонтальная — и.

4. Находят моменты инерции сечения относительно главных центральных осей. В общем виде моменты инерции сечения оп­ределяют по формулам:

относительно оси и

относительно оси v

38

Если главная центральная ось совпадает с собственной цен­тральной осью какого-нибудь профиля или фигуры, то момент инерции ее относительно главной центральной оси равен мо­менту инерции относительно собственной оси, так как расстоя­ние между ними равно нулю.

При определении геометрических характеристик необходимо учитывать, что профили проката на заданном сечении могут быть ориентированы иначе, чем в ГОСТах. Например, верти­кальная по ГОСТу ocь у на заданном сечении может оказаться горизонтальной, а горизонтальная ось х — вертикальной. Поэто­му необходимо внимательно следить за тем, относительно каких осей следует брать геометрические характеристики. На это будет обращено особое внимание в рассматриваемых примерах.

Пример 9. Определить главные моменты инерции сечения, показанного на рис. 13. Сечение состоит из двух уголков 56x4 и швеллера № 18.

39

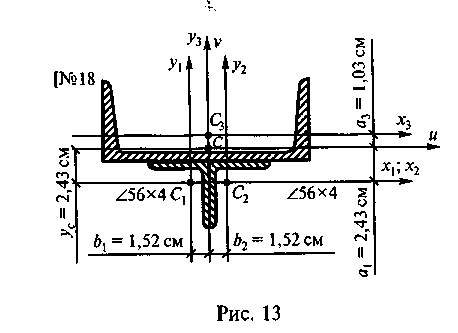
Решение. 1. Определим положение центра тяжести сечения (см. пример 5). Координаты центра тяжести: х_с= 0; у_с= 2,43 см.

2. Проведем центральные оси х_ъ х₂, х₃ и оси у_ъ у₂, у$ через центры тяжести фигур 1, 2, 3.

3. Проведем главные центральные оси. Ось v совместим с осью симметрии у₃. Ось проведем через центр тяжести сечения С перпендикулярно оси v. Оси v и у₃ совпали.

4. Определим главный момент инерции относительно оси и:

Из рис. 13 следует, что уголки одинаковые и расположе­ны на одинаковом расстоянии от оси и, т. е. А\ = А₂ и а_{ = а₂. Поэтому формулу для определения /„ можно записать:

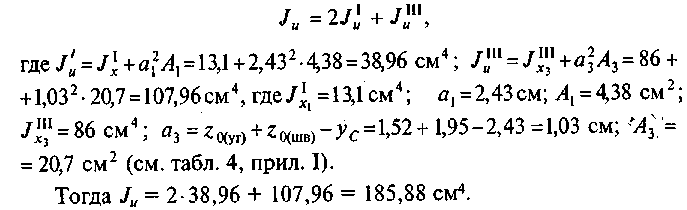
Определим главный момент инерции относительно оси v:

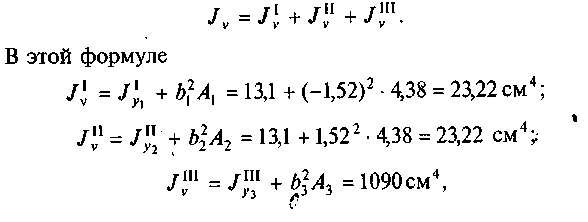
40

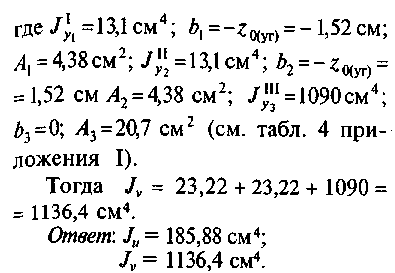
Пример 10. Определить момент инерции сечения, показанного на рис. 14, относительно главной центральной оси, не являющейся осью симметрии сечения. Сечение состоит из двутавра № 24 и швеллера № 24а.

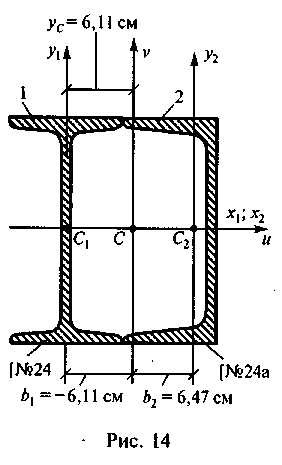
Решение. 1. Центр тяжести сече­ния найден в примере 7 (х_с = 6,11 см; Ус = 0).

2. Проведем центральные оси х_ь х₂ и у_ъ у₂. Оси x_l и х₂ совпали.

3. Проведем главные центральные оси. Ось и совмещаем с осью симметрии, а ось v проводим через центр тяжести С пер­пендикулярно оси и. Оси и, х_г и х₂ совпали.

4. Определим момент инерции сечения относительно оси v, так как по условию требуется найти момент инерции только отно­сительно оси, не являющейся осью симметрии. Запишем фор­мулу

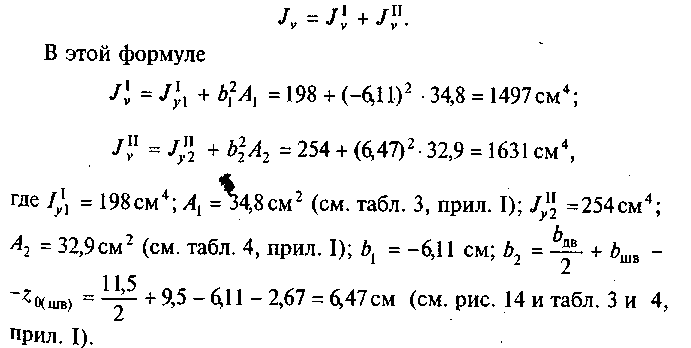
Тогда /_v= 1497 + 1631 = 3128 см⁴. Ответ: J_v = 312% см⁴

Задание для самостоятельной работы 5. Определить момент инерциш сечения относительно главной центральной оси, не являющейся осью] симметрии, по данным одного из вариантов, показанных на рис. 10. }