1.3. Определение положения центра тяжести сечения

1. Разбивают сечение на простые фигуры. В задачах для само­стоятельной работы такими фигурами являются стандартные профили проката, размеры которых приведены в прил. I. Обыч­но профили прокатной стали, образующие сечение, обозначают цифрами 1, 2, 3, ... .

2. Указывают центры тяжести каждого профиля (фигуры) и обо­значают их C₁, ..., С_N , используя таблицы ГОСТов (см. прил. I).

3. Выбирают систему координатных осей. В задачах для само­стоятельной работы все сечения имеют одну ось симметрии, по­этому рекомендуется одну из координатных осей совмещать с ней. Вторую ось координат направляют перпендикулярно первой так, чтобы она пересекла центры тяжести одной или нескольких фигур. При этом начало координат может совпадать (или не сов­падать) с центром тяжести одной из фигур. Вторую ось можно направить так, чтобы она прошла через нижнюю (крайнюю) точ­ку сечения. В первом случае вычисления будут более простыми.

4. Составляют формулы для определения координат центра тя­жести сечения:

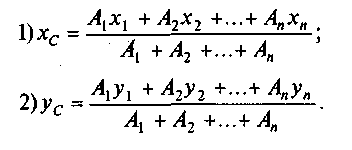
22

Пользуясь таблицами ГОСТов (см. прил. I), определяют пло­щади профилей проката А_ъ А₂, ..., А„, координаты их центров тя­жести х_{, х₂, ...,х„ и у_ъ у₂, ...,у„ относительно выбранных осей координат. Число слагаемых в числителе и знаменателе формул зависит от числа профилей, из которых состоит сечение. Полу­ченные величины подставляют в формулу и находят х_с и у_с.

Следует помнить, что если ось х совмещена с осью симмет­рии, то координата у_с = 0, а если ось у совмещена с осью сим­метрии, то х_с = 0.

5. Указывают положение центра тяжести на рисунке, придер­живаясь определенного масштаба, и показывают расстояние от центра тяжести до координатных осей.

6. Выполняют проверку правильности решения, для чего можно изменить положение координатных осей (или одной оси) и най­ти координаты центра тяжести относительно .новых осей. Поло­жение центра тяжести не зависит от того, как выбрана система координатных осей.

Пример 5. Определить координаты центра тяжести сечения, по­казанного на рис. 8, а. Сечение состоит из двух уголков (/.} 56x4 и швеллера ([) № 18. Выполнить проверку правильности определения положения центра тяжести. Указать его положение на сечении.

Решение. 1. Разобьем сечение на профили проката: два уголка 56x4 и швеллер № 18. Обозначим их 1, 2, 3 (см. рис. 8, а).

2. Укажем центры тяжести каждого профиля, используя табл. 1 и 4 прил. I, и обозначим их Q, С₂, С₃.

3. Выберем систему координатных осей. Ось у совместим с осью симметрии, а ось х проведем через центры тяжести уголков.

4. Определим координаты центра тяжести всего сечения. Так как ось у совпадает с осью симметрии, то она проходит через центр тяжести сечения, поэтому х_с = 0. Координату у_с опреде­лим по формуле

Пользуясь табл. 1 и 4 прил. I, определим площади каждого профиля и координаты центров тяжести:

Координаты yi и у2 равны нулю, так как ось х проходит через центры тяжести уголков. Подставим полученные значения в формулу для определения у_с:

23

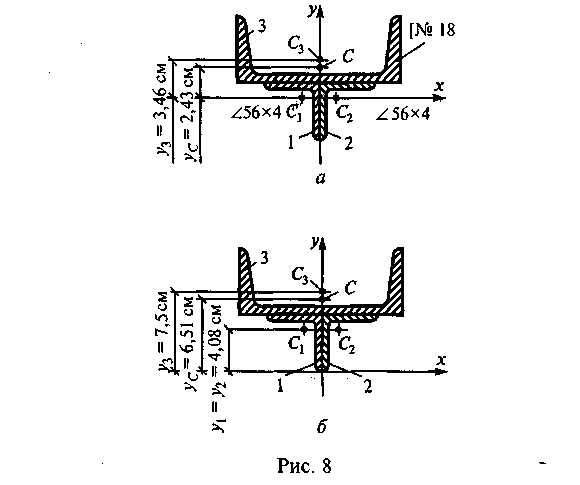
5. Укажем центр тяжести сечения на рис. 8, а и обозначим его буквой С. Покажем расстояние у с = 2,43 см от оси х до точ­ки С.

Поскольку уголки симметрично расположены, имеют одина­ковую площадь и координаты, то А] = А₂, y_l = у₂. Поэтому фор­мула для определения у_с может быть упрощена:

6. Выполним проверку. Для этого ось х проведем по нижнему краю полки уголка (рис. 8, б). Ось у оставим, как в первом ре­шении. Формулы для определения хс и у_с не изменяются:

Площади профилей останутся такими же, а координаты центров тяжестей уголков и швеллера изменятся. Выпишем их:

Находим координату центра тяжести:

24

По найденным координатам х_с и у_с наносим на рисунок точ­ку С. Найденное двумя способами положение центра тяжести находится в одной и той же точке. Проверим это. Разница между координатами у_с, найденными при первом и втором решении, составляет: 6,51 - 2,43 = 4,08 см.

Это равно расстоянию между осями х при первом и втором решении: 5,6 - 1,52 = 4,08 см.

Ответ: у_с = 2,43 см, если ось jc проходит через центры тяже­сти уголков, или у_с = 6,51 см, если ось х проходит по нижнему краю полки уголка.

Пример 6. Определить координаты центра тяжести сечения, изображенного на рис. 9, а. Сечение состоит из двутавра (I) № 24 и швеллера № 24а. Показать положение центра тяжести на сече­нии.

Решение. 1. Разобьем сечение на профили проката: двутавр и швеллер. Обозначим их цифрами 1 и 2.

2. Укажем центры тяжести каждого профиля С\ и С₂, ис­пользуя табл. 3 и 4 прил. I.

3. Выберем систему осей координат. Ось х совместим с осью симметрии, а ось у проведем через центр тяжести двутавра.

4. Определим координаты центра тяжести сечения. Координа­та у_с = 0, так как ось х совпадает с осью симметрии. Координату х_с определим по формуле

25

По табл. 3 и 4 прил. I и схеме сечения определим

Подставим числовые значения в формулу и получим

5. Нанесем точку С (центр тяжести сечения) по найденным значениям х_с и у_с (см. рис. 9, а).

6. Проверку решения необходимо выполнить самостоятельно при положении осей, как показано на рис. 9, б. В результате ре­шения получим х_с - 11,86 см. Разница между значениями х_с при первом и втором решении равна 11,86 - 6,11 = 5,75 см, что равно расстоянию между осями у при тех же решениях b_дв/2 = 5,75 см.

Ответ: х_с = 6,11 см, если ось у проходит через центр тяжести двутавра; х_с = 11,86 см, если ось у проходит через левые крайние точки двутавра.

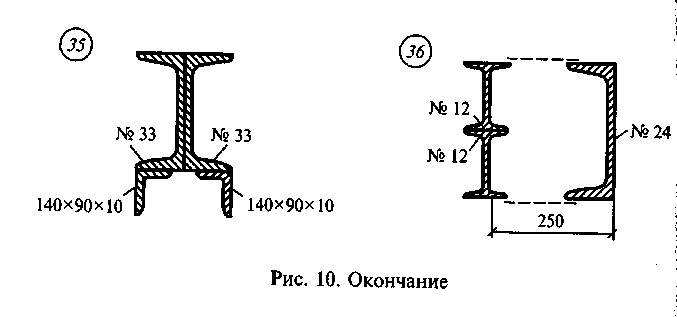
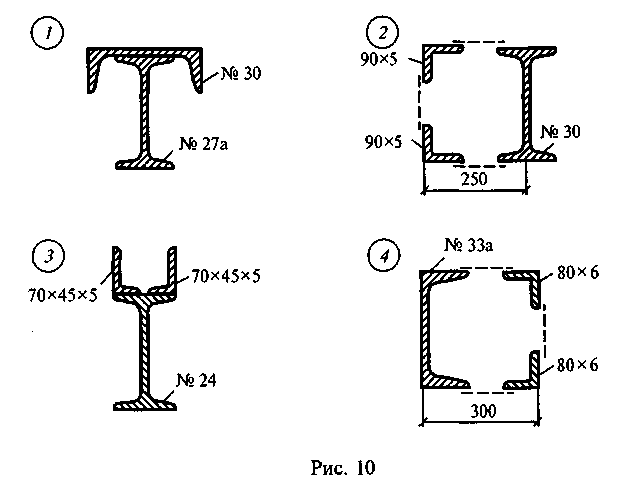
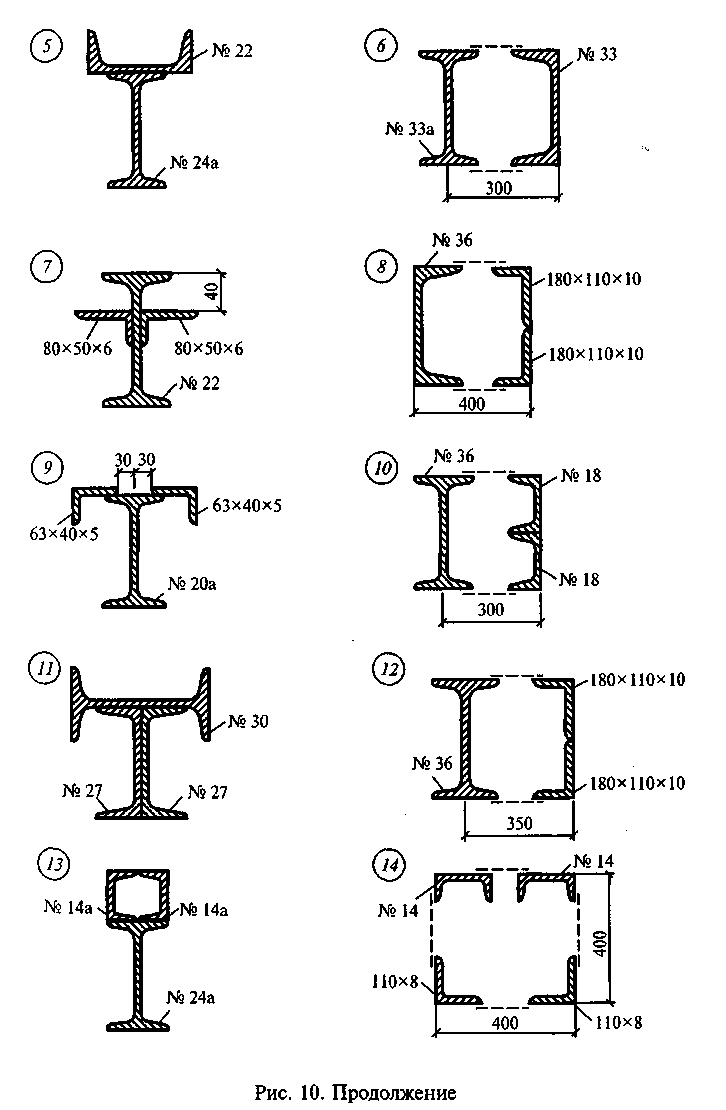
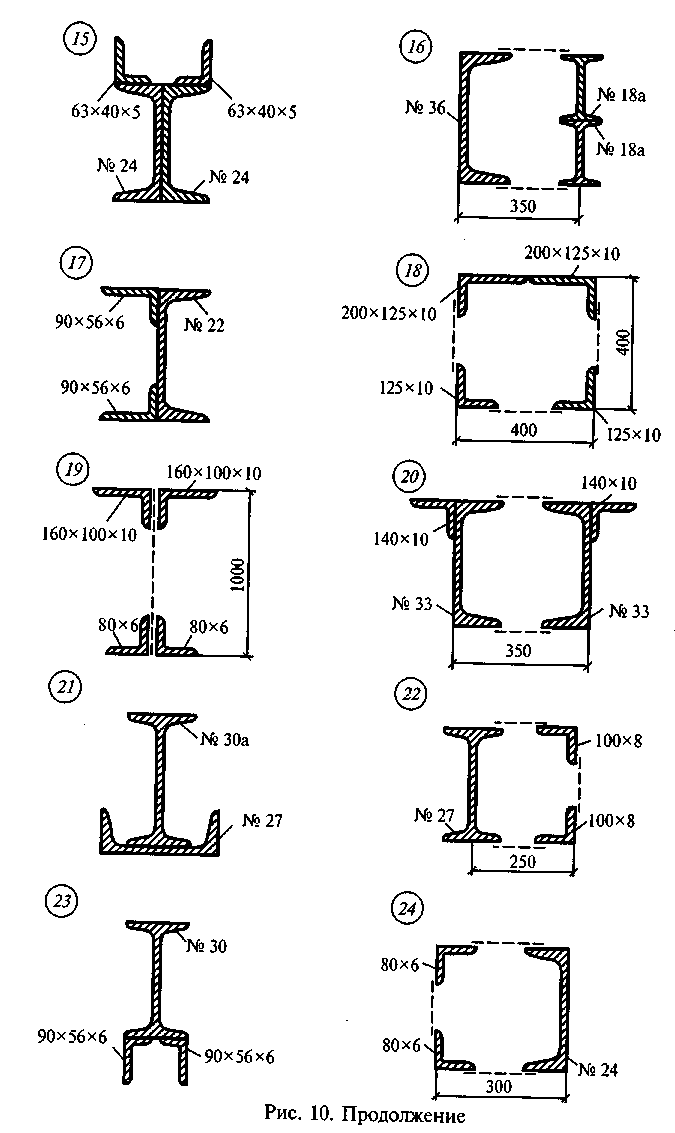
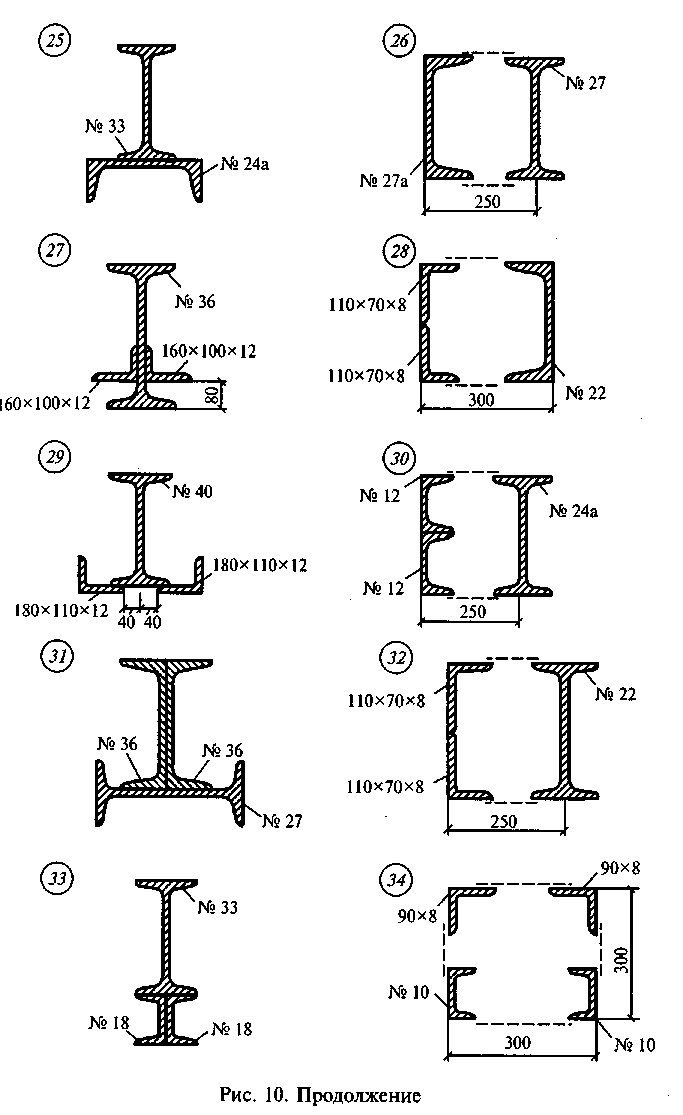
Задание для самостоятельной работы 3. Определить координаты цен­тра тяжести сечения по данным одного из вариантов, показанных на рис. 10. Показать положение центра тяжести на сечении.

26

27

28

29