
- •Раздел I самостоятельные и контрольные работы
- •Глава 1 теоретическая механика. Статика
- •1.1. Определение реакций идеальных связей аналитическим способом
- •1.2. Определение опорных реакций балки на двух опорах при действии вертикальных нагрузок
- •1.3. Определение положения центра тяжести сечения
- •Глава 2 сопротивление материалов
- •2.1. Подбор сечений стержней из расчета на прочность
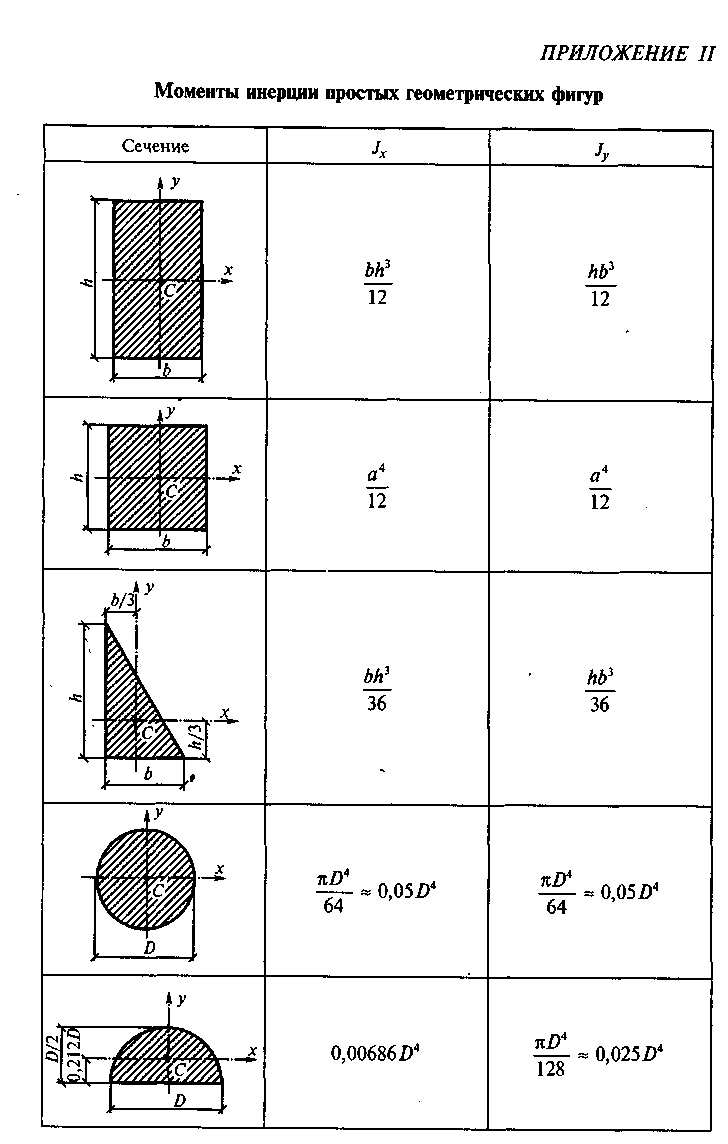
- •2.2. Определение главных центральных моментов инерции сечения
- •2.3. Построение эпюр поперечных сил и изгибающих моментов для простой балки
- •2.4. Определение допустимого значения центрально-сжимающей силы
- •Глава 3 статика сооружений
- •3.1. Построение эпюр внутренних усилий для простейшей одноконтурной рамы
- •3.2. Графическое определение усилий в стержнях фермы построением диаграммы Максвелла—Кремоны
- •3.3. Определение линейных перемещений в простейших консольных рамах
- •3.4. Расчет статически неопределимой (неразрезной) балки по уравнению трех моментов
- •Раздел II расчетно-графические работы
- •Глава 4 теоретическая механика. Статика
- •4.1. Определение усилий в стержнях простейшей консольной фермы
- •4.2. Определение опорных реакций балки на двух опорах
- •4.3. Определение положения j центра тяжести сечения
- •5.1. Определение усилий в стержнях статически
- •5.2. Определение главных моментов инерции сечения
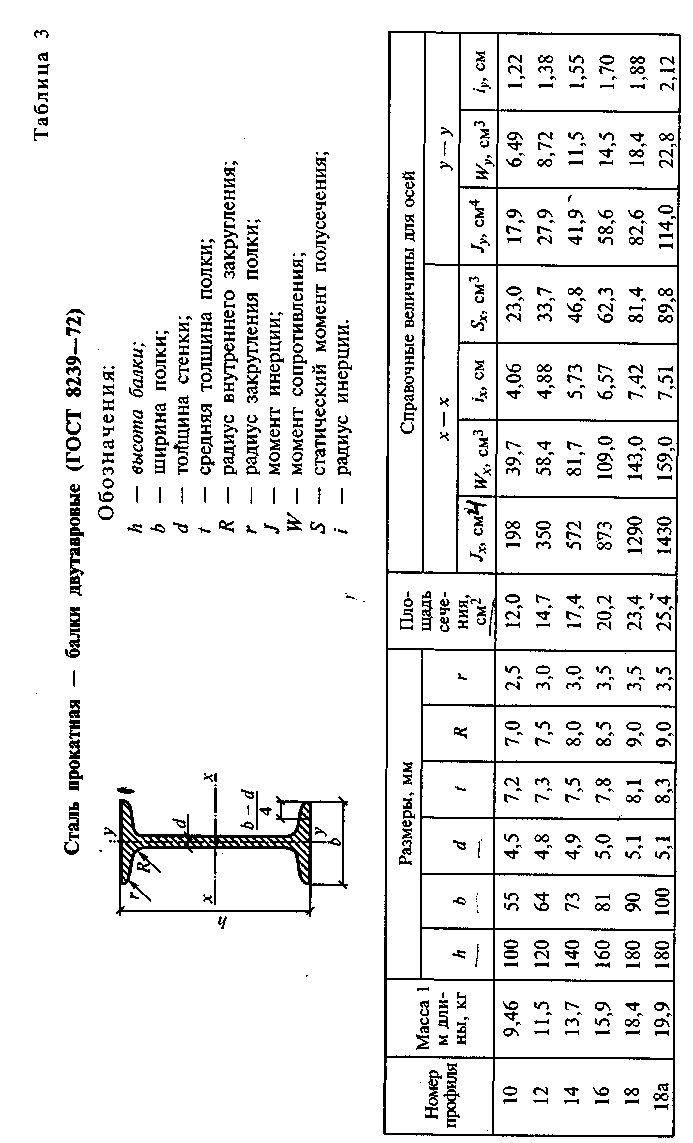
- •5.3. Подбор сечения балки из прокатного двутавра
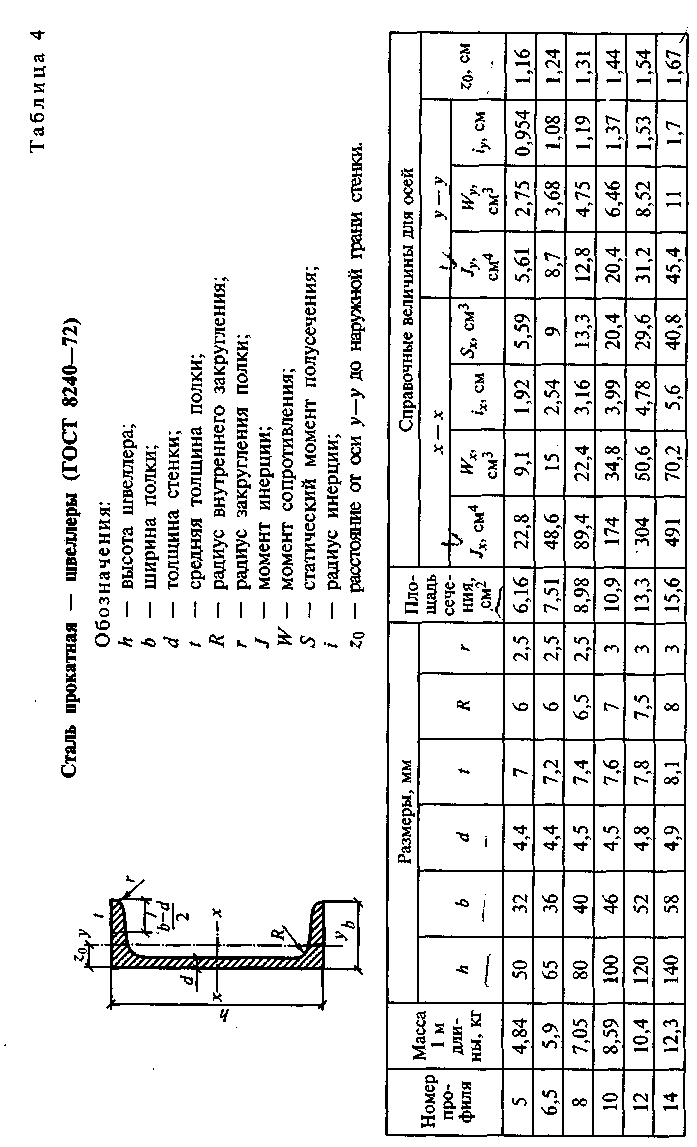
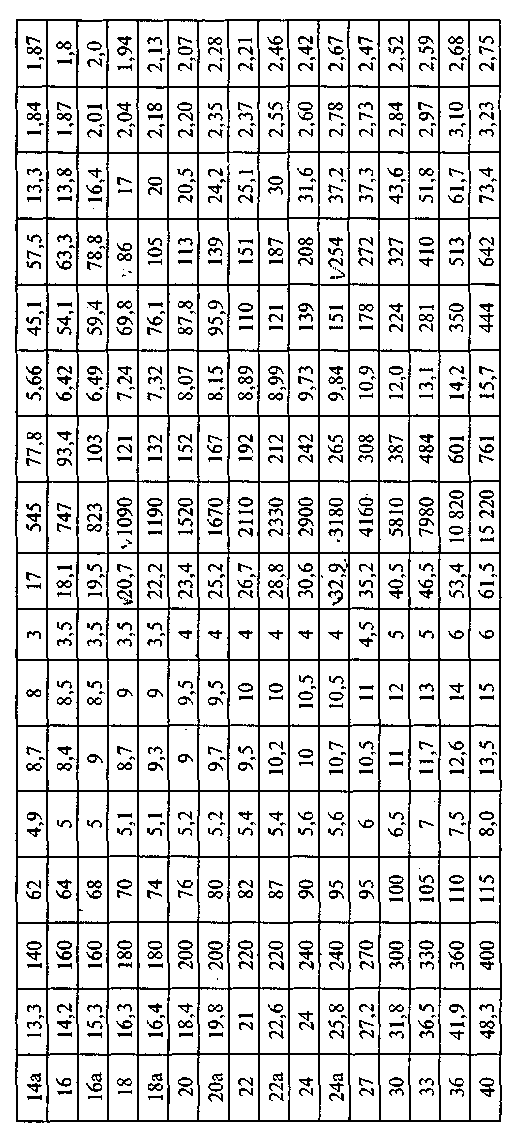
- •5.4. Подбор сечения центрально-сжатой составной стойки
- •Глава 6 статика сооружений
- •6.1. Определение усилий в сечениях трехшарнирной арки
- •6.2. Графическое определение усилий в стержнях
- •6.3. Расчет статически неопределимой рамы
- •6.4. Расчет неразрезной балки по уравнению трех моментов
- •Глава 4. Теоретическая механика. Статика ....................101
- •Глава 5. Сопротивление материалов ......................... 130
- •Глава 6. Статика сооружений .............................. 157
6.4. Расчет неразрезной балки по уравнению трех моментов
К решению задачи рекомендуется приступить после выполнения самостоятельной работы 11. Порядок решения остается таким же.
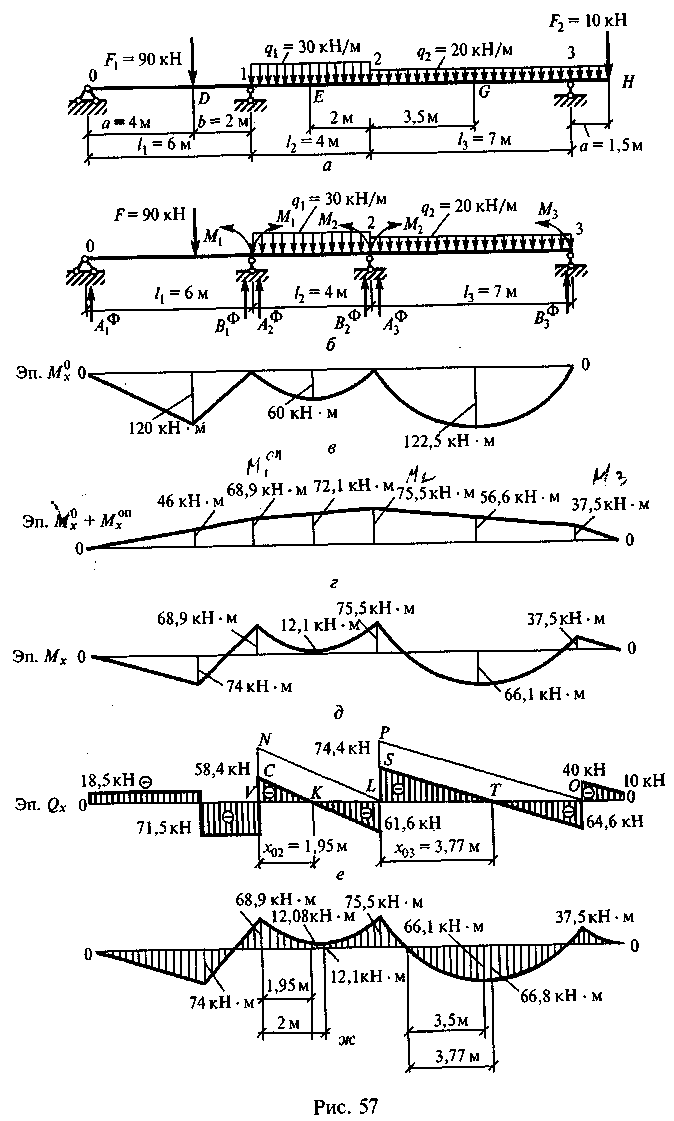
Пример 37. Построить эпюры Qx и Мх для неразрезной балки, показанной на рис. 57, а.
Решение. 1. Обозначим пролеты 1Ь 12, 13 и опоры О, 1, 2, 3.
2. От заданной системы переходим к основной. Вместо опор вводим шарниры и заменяем действие отброшенных связей опорными моментами М0, М1, М2 и М3. Консоль в основной системе отбросим (рис. 57, б). Фиктивные опорные реакции на основной системе показаны условно.
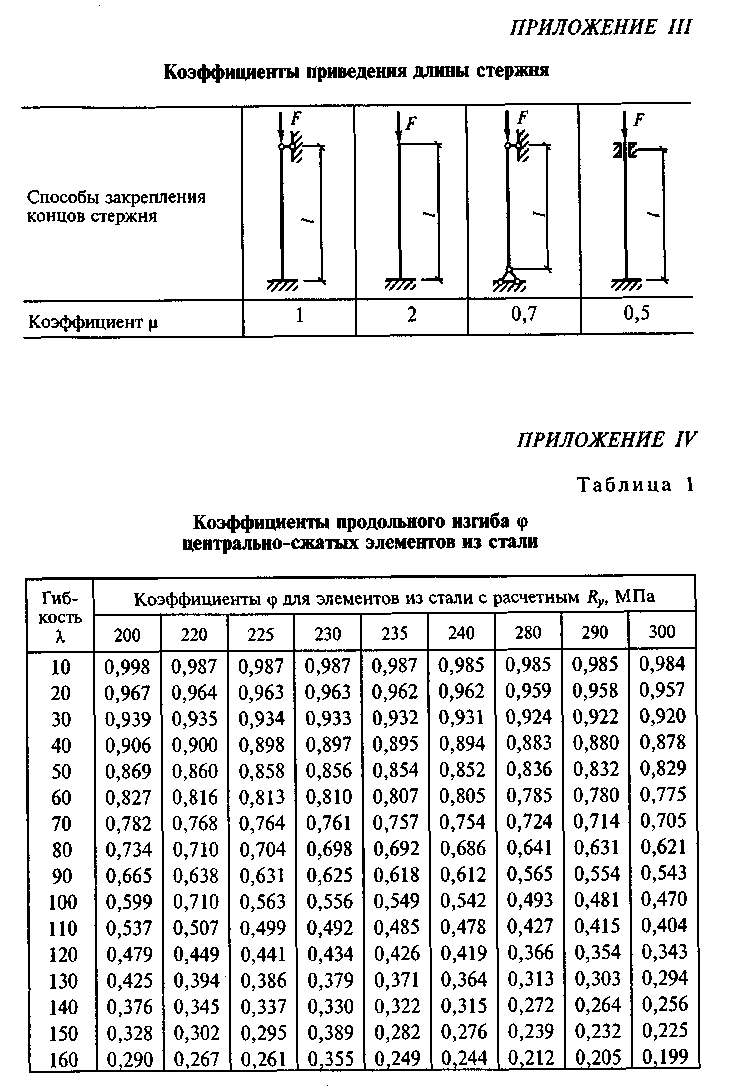
3. Определим значения изгибающих моментов М0х от заданной нагрузки для основной системы (см. прил. V):

По найденным значениям строим эпюру М°х (рис. 57, в).
190
191
4. Составим уравнения трех моментов. Таких уравнений будет два^для промежуточных опор 1 и 2.
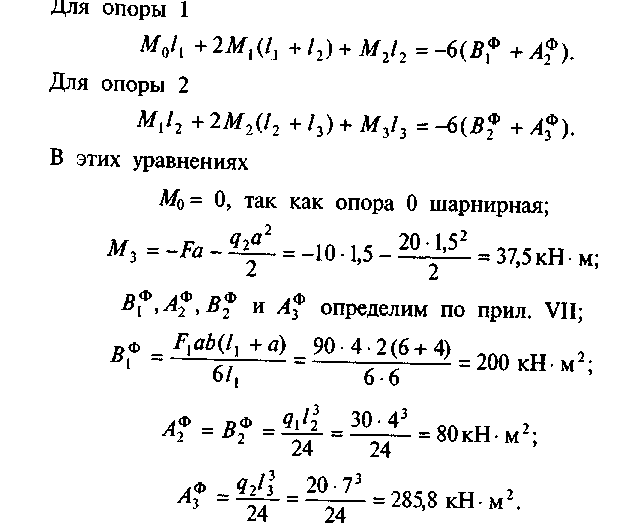
Подставим найденные значения в уравнения трех моментов:
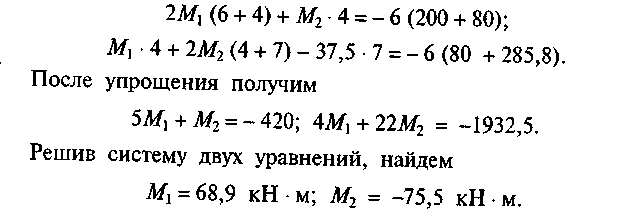
В целях единообразия дальнейших вычислений обозначим эт) моменты М1°п и М2°п.
5. По найденным значениям строим эпюру моментов Мх°п (см. рис. 57, в), откладывая значения моментов М1°п , М2°п и М3ОП на опорах в отрицательную сторону и соединяя концы отрезков прямыми линиями.
6. Определяем значения изгибающих моментов для заданной системы от заданной нагрузки в характерных точках путем суммиро вания значений эпюр М0х и Мх°П (рис. 57, г):
![]()
192

По найденным значениям строим эпюру Мх (рис. 57, д). Значения моментов во втором и третьем пролетах не являются экстремальными. Они будут уточнены после построения эпюры Qx.
1. Определим значения поперечных, сил на n-й опоре по формулам (см. прил. VI):
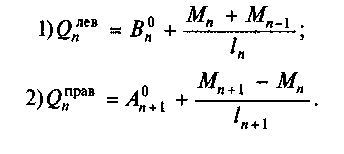
193
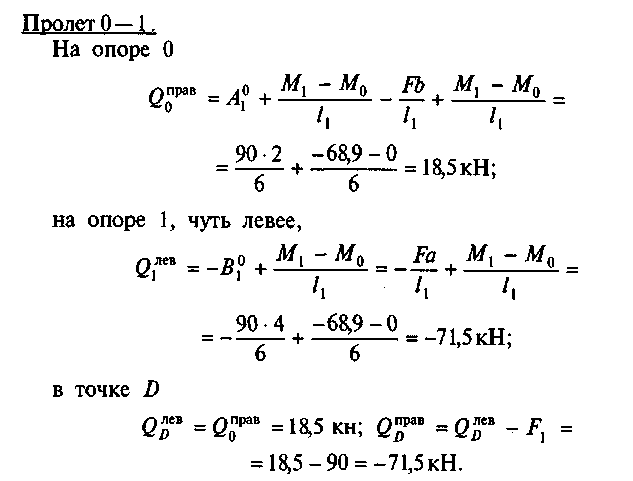
На участках 0D и D1 эпюра Qx представляет собой прямую линию, параллельную нулевой.
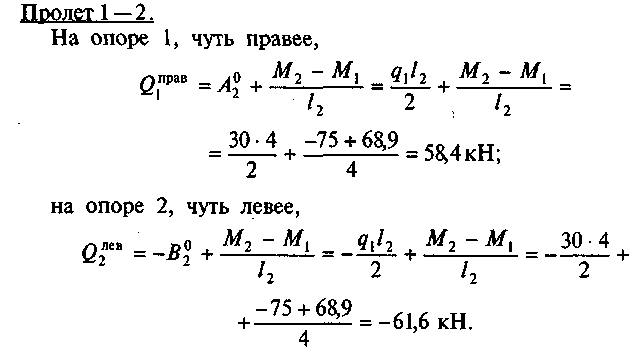
В пролете 1—2 эпюра Qx — прямая линия, наклонная к нулевой и пересекающая ее. Определим положение точки К, в которой эпюра Qx пересекает нулевую линию. Из подобия треугольников VCK и VNL

194
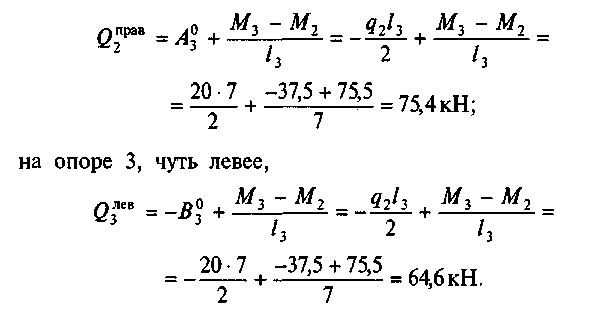
В пролете 2 — 3 эпюра Qx — прямая линия, наклонная к нулевой. Она пересекает нулевую линию в точке Т. Определим положение этой точки из подобия треугольников STL и POL:
X03: 7 = 75,4 : 140; откуда х03 = (75,4 • 4)/140 = 3,77 м.
Консоль 3— G.
На опоре 3 (чуть правее) поперечную силу найдем из суммы проекций всех правых сил на ось у:
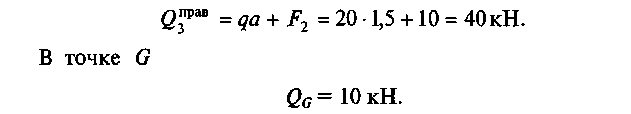
По найденным значениям строим эпюру Qx (рис. 57, е).
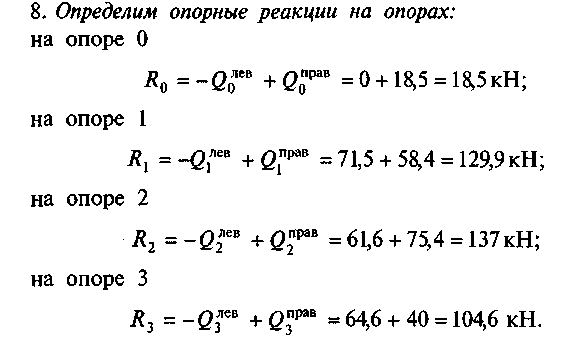
9. Проверим правильность определения опорных реакций по урав-
нению
![]()
или 18,5 + 129,9 + 137 + 104,6 - 90 - 30 • 4 - 20 • 8,5 -
-10 = 0, откуда 390 - 390 = 0.
195
10. Уточним эпюру Мх. Определим изгибающий момент в сечении на расстоянии х02 - 1,95 м от опоры 1:

Определим изгибающий момент в сечении на расстоянии х03 = = 3,77 м от опоры 2. Рассмотрим правую часть балки:
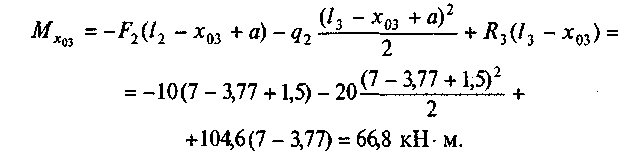
Построим эпюру Мх с уточненными значениями моментов (рис. 57, ж).
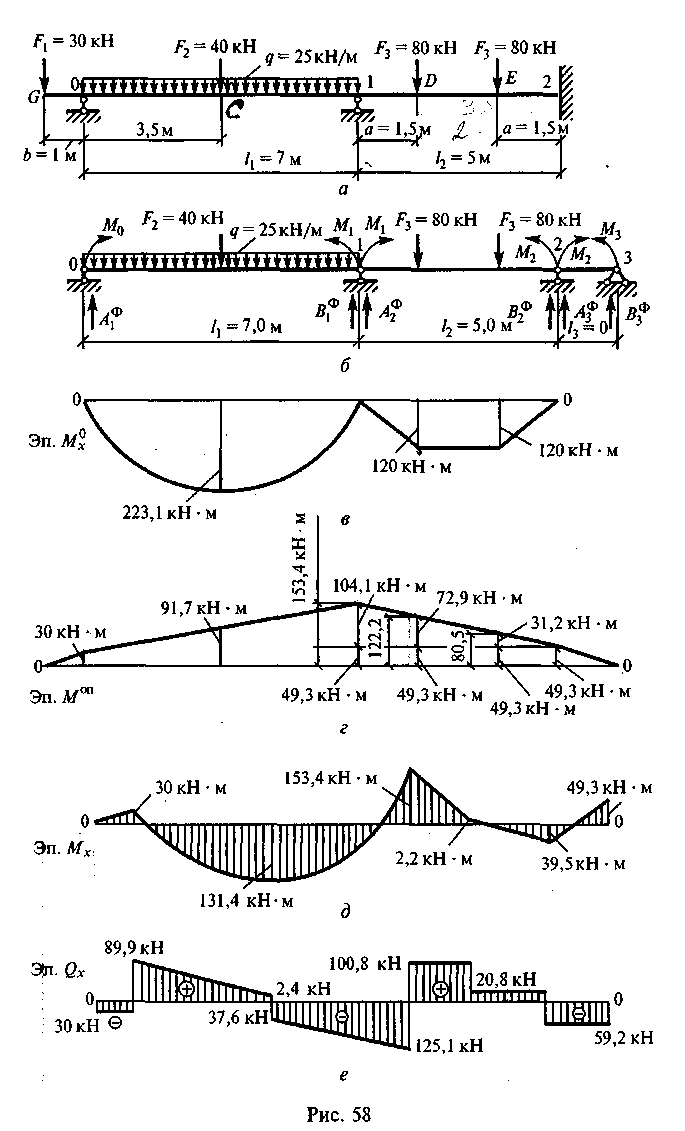
Пример 38. Построить эпюры Мх и Qx для неразрезной балки, показанной на рис. 58, а.
Решение. 1. Обозначим пролеты /,, 12 и опоры О, 1, 2.
2. Выберем основную систему. На опоры введем шарниры и обозначим опорные моменты М0, М1 и М2. Для получения уравнений трех моментов вместо жесткой заделки введем еще один (фиктивный) пролет /3 = 0 и опору 3 с опорным моментом М3 = О (рис. 58, б).
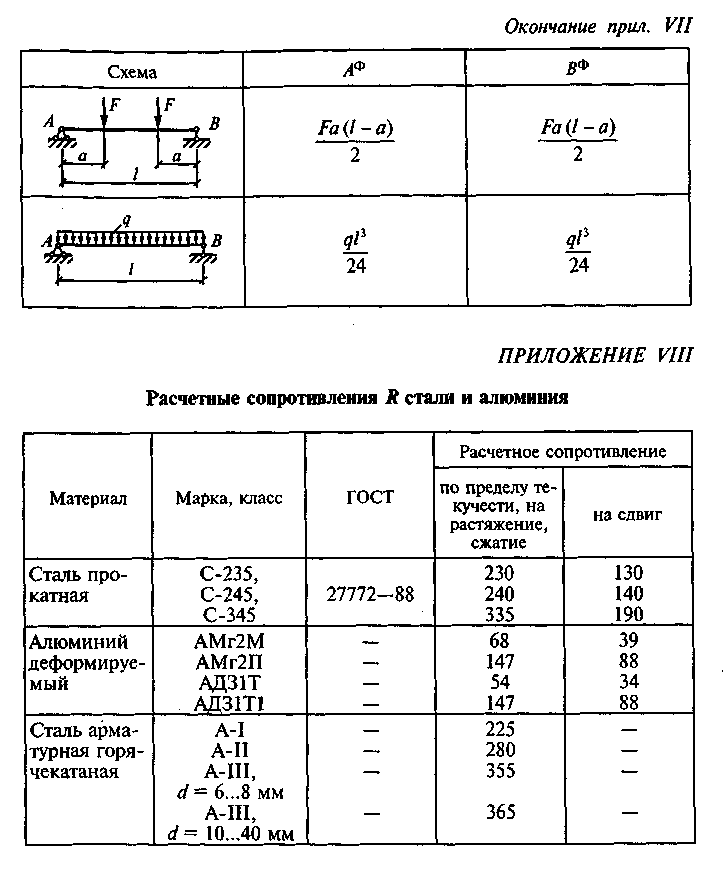
3. Определим величины изгибающих моментов для основной системы от заданной нагрузки (см. прил. VI).
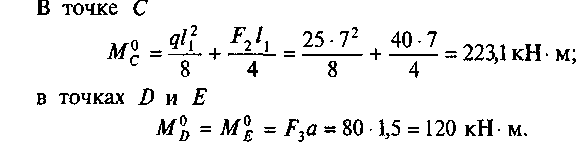
По найденным значениям строим эпюру М0х (рис. 58, в).
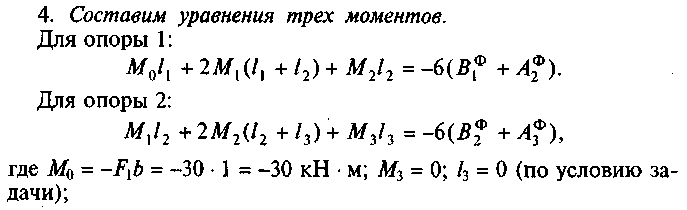
196
197
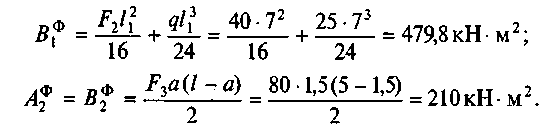
(прил. VIII).
Подставим полученные значения в уравнения трех моментов:
![]()
После упрощения получим
24М1 + 5М2 = - 3928,8; 5М1 + 10М2 = -1260.
Решив совместно оба уравнения, получим М1 = -153,4 кН • м; М2 = -49,3 кНм.
5. По найденным значениям строим эпюру опорных моментов Моп(рис. 58, г). Определим опорные моменты. ,/ /
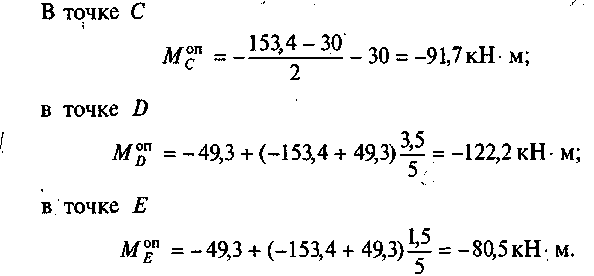
6. Определим значения Мх от заданной нагрузки для заданной схемы путем суммирования эпюр Мх° и Мхоп:
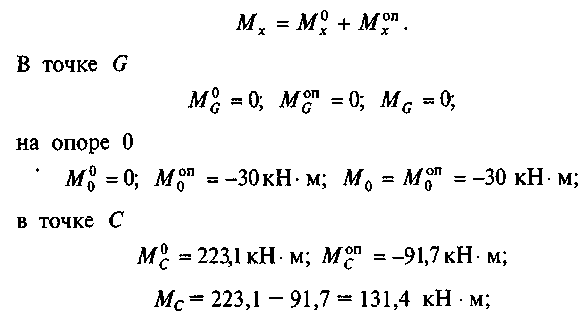
198
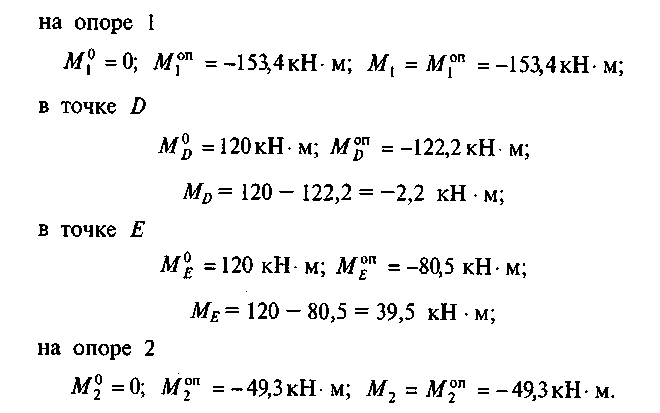
По найденным значениям строим эпюру Мх (рис. 58, д). 7. Определим значения поперечных сил в характерных точках.
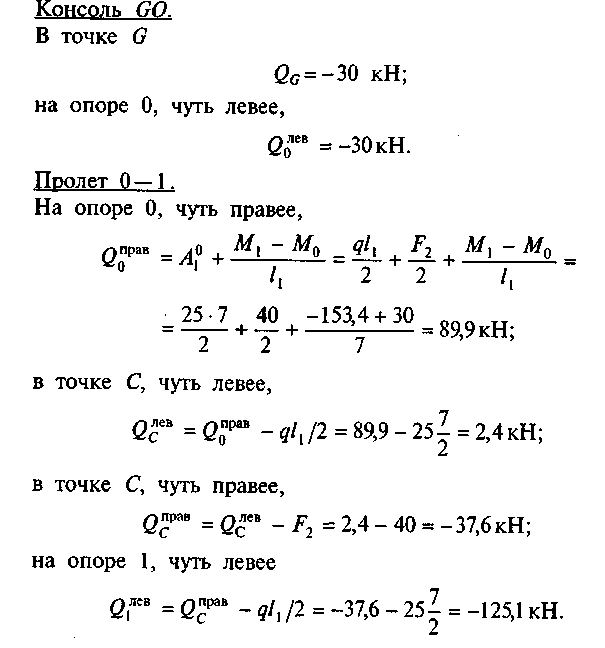
199

По найденным значениям строим эпюру Qx (рис. 58, е). 8. Определим опорные реакции:
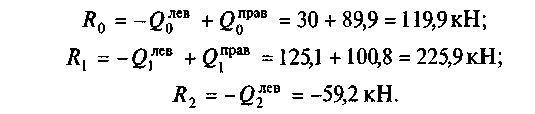
9. Проверим правильность определения опорных реакций:
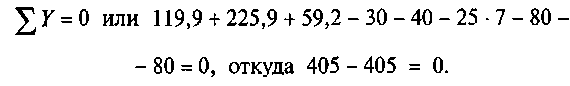
В качестве проверки всего решения необходимо найти момент в любой (лучше нескольких) точке балки, рассматривая левую или правую ее часть. Определим момент, например в точке С.
Рассмотрим левую часть балки:
![]()
![]()
200
Рассмотрим правую часть балки:
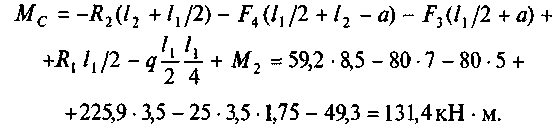
Моменты от правых и левых сил получились одинаковыми:
![]()
Оба эти момента равны моменту в точке С на эпюре Мх.
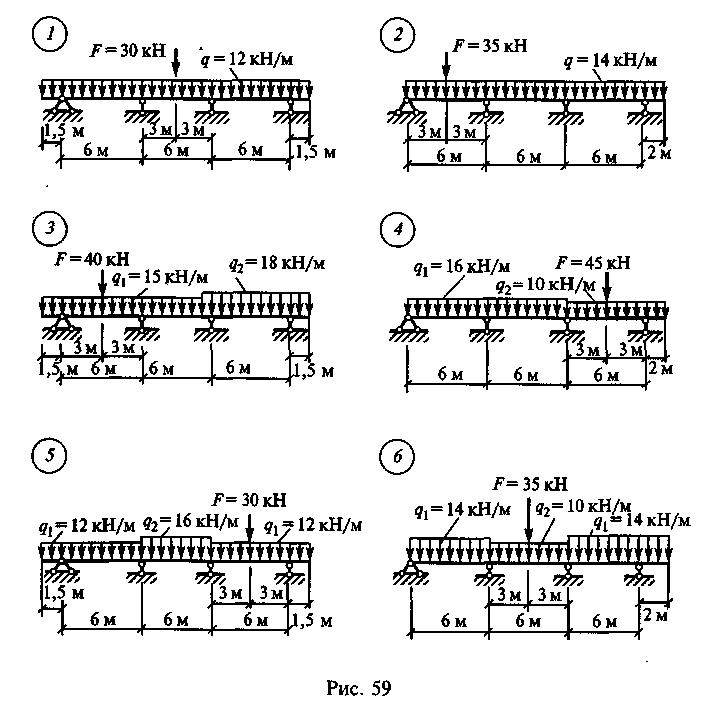
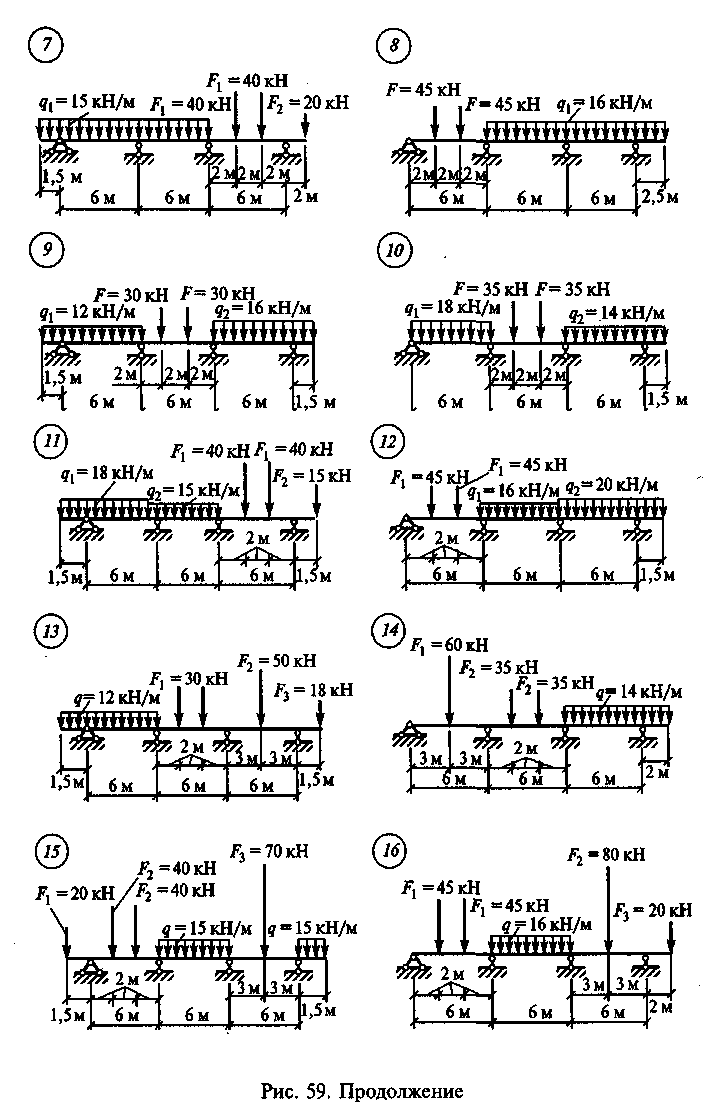
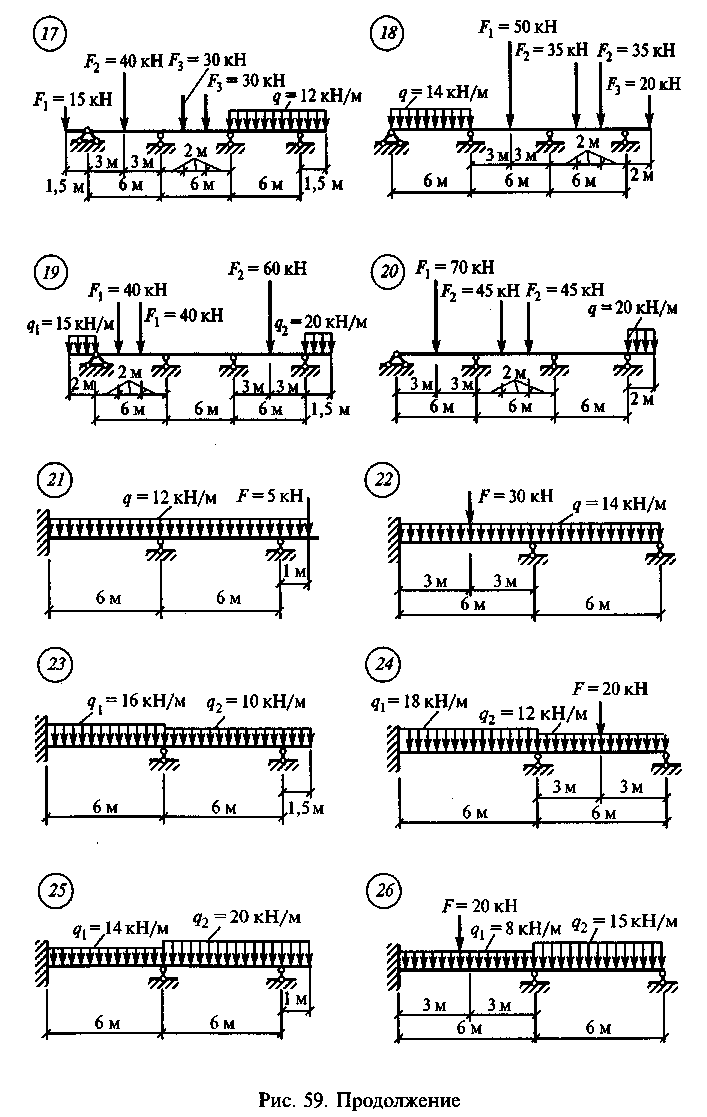
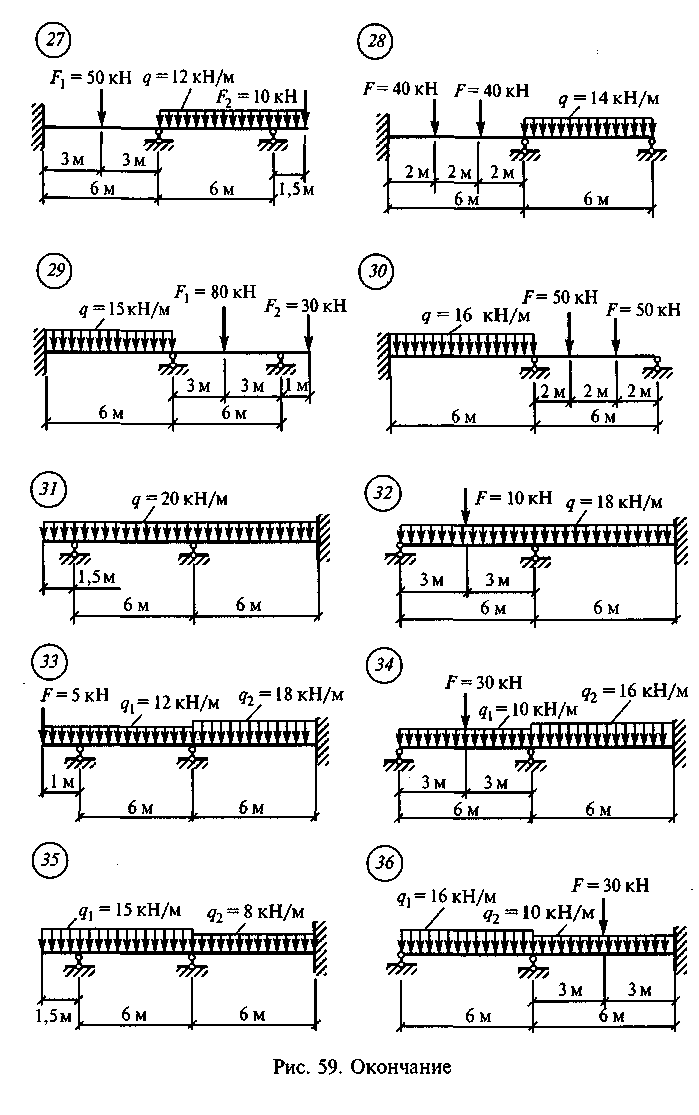
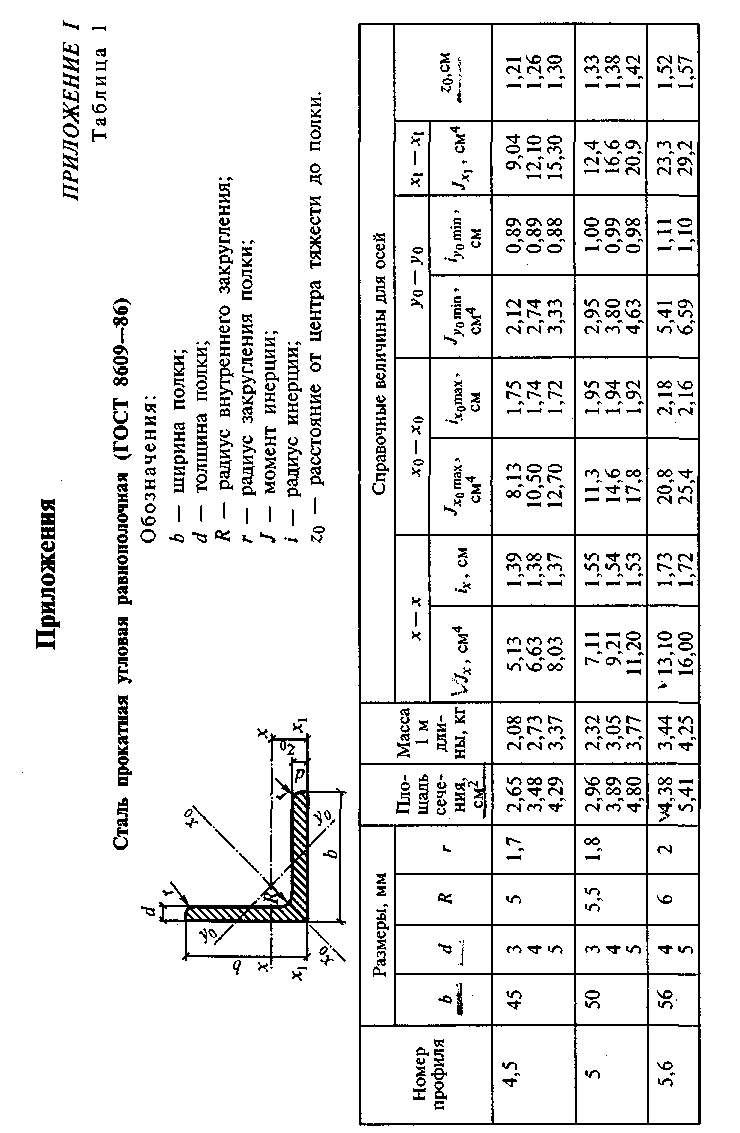
Задание для расчетно-графической работы 11. Построить эпюры Qx и Мх для неразрезной балки по данным одного из вариантов, приведенных на рис. 59.
201
202
203
205
206
207
208
209
210
211
212

213
214
215
216
217
218
219
220
СПИСОК ЛИТЕРАТУРЫ
1. Аркуша А.И. Руководство к решению задач по теоретической механике. — М.: Высшая школа, 1976. — 288 с.
2. Михайлов А.М. Основы расчета элементов строительных конструкций в примерах. — М.: Высшая школа, 1986. — 416 с. ' 3. Мухин А.В. Статика сооружений в примерах. —М.: Высшая школа 1979. - 304 с.
4. Портаев Л.П., Петраков А.А., Портаев В.Л. Техническая механика. — М.: Стройиздат, 1987. — 464 с.
5. Улитин Н.С., Першин А.Н., Лауенбург Л.В. Сборник задач по технической механике. — М.: Высшая школа, 1978. — 399 с.
6. СНиП П-23-81*. Стальные конструкции. —М.: Минстрой России 1995.-96 с.
7. СНиП 2.03.09-85. Алюминиевые конструкции — М • Стройиздат 1984.-46 с.
8. СН 528-80. Перечень единиц физических величин, подлежащих применению в строительстве. — М.: Стройиздат, 1981. — 34 с.
ОГЛАВЛЕНИЕ
Предисловие ............................................ 3
Раздел I. Самостоятельные и контрольные работы. ................ 5
Глава 1. Теоретическая механика. Статика ...................... 5
1.1. Определение реакций идеальных связей аналитическим
способом .............................. 5
1.2. Определение опорных реакций балки на двух опорах
при действии вертикальных нагрузок ............. 15
1.3. Определение положения центра тяжести сечения ...... 22
Глава 2. Сопротивление материалов .......................... 31
2.1. Подбор сечений стержней из расчета на прочность. .... 31
2.2. Определение главных центральных моментов инерции
сечения .............................. 38
2.3. Построение эпюр поперечных сил и изгибающих моментов для простой балки ........................ 42
2.4. Определение допустимого значения центрально-сжимающей силы ................................ 53
Глава 3. Статика сооружений ............................... 61
3.1. Построение эпюр внутренних усилий для простейшей
одноконтурной рамы. ...................... 61
3.2. Графическое определение усилий в стержнях фермы
построением диаграммы Максвелла —Кремоны. ....... 71
3.3. Определение линейных перемещений в простейших
консольных рамах ........................ 80
3.4. Расчет статически неопределимой (неразрезной) балки
по уравнению трех моментов. ................. 90
Раздел П. Расчетно-графические работы ....................... 101
