6.3. Расчет статически неопределимой рамы

1. Определяют степень статической неопределимости системы: Л = 2Ш + С_оп - ЗД,

где Ш — число промежуточных шарниров в раме; С_оп — число опорных стержней, крепящих раму к основанию; шарнирно-подвижная опора имеет один опорный стержень, шарнирно-неподвижная — два, жесткая защемляющая — три; Д — число жестких дисков, образующих систему.

Степень статической неопределимости системы равна числу лишних связей. В задачах для расчетно-графической работы приведены дважды статически неопределимые рамы. В этом следует убедиться.

2. Выбирают основную систему, которую лучше иметь статически определимой. Для этого необходимо отбросить лишние связи и заменить их действие неизвестными пока реакциями. В задачах для расчетной графической работы есть возможность основную систему получить в виде консольной рамы или бруса с ломаной осью, отбрасывая две связи и заменяя их действие реакциями, которые обозначают Х_{ и Х₂.

3. Определяют изгибающие моменты в характерных точках от заданной нагрузки для основной системы и строят эпюру моментов. Эта эпюра называется грузовой и обозначается M_F.

4. Строят эпюры моментов от единичных сил X_t =1 и Х ₂_^_ = 1. Эти эпюры называются единичными и обозначаются M₁ и М₂.

5. Составляют канонические уравнения метода сил. Число уравнений зависит от степени статической неопределимости системы (числа неизвестных). Для системы с двумя неизвестными уравнения принимают вид:

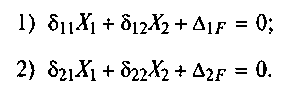
Определяют коэффициенты при неизвестных путем перемно­жения единичных эпюр и свободные члены путем перемножения единичных эпюр на грузовую эпюру. При этом следует пользо­ваться прил. V. Из уравнений находят неизвестные Х₁ и Х₂.

6. Строят эпюры моментов от найденных сил M_Xl и M_Xi, умно­жая значения эпюр М₁ и M₂ на Х_} и Х₂.

7. Определяют изгибающие моменты в характерных точках от заданной нагрузки для заданной системы путем суммирования зна­чений моментов эпюр M_F, М_х и М_х .

На этом решение задачи заканчивается. Построение эпюр Q_x, N_x и выполнение деформационной проверки выходит за рамки задачи. Они могут быть построены по правилам, приведенным в самостоятельной работе 8.

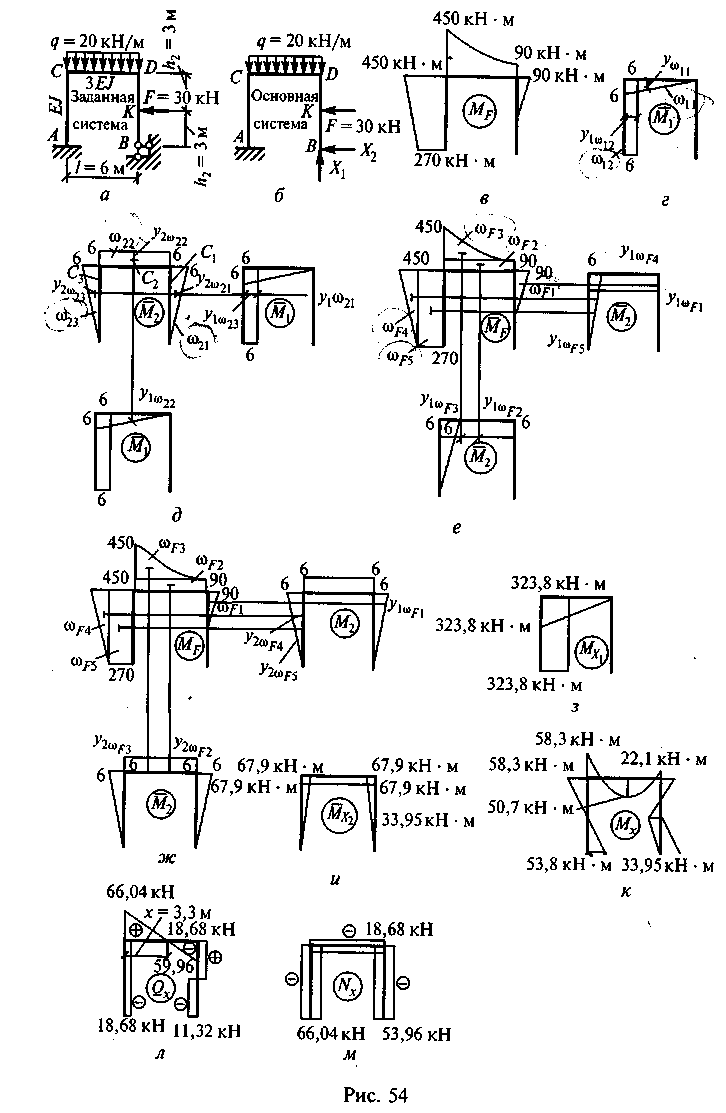
Пример 35. Построить эпюру М_х для рамы, показанной на рис. 54, а.

Решение. 1. Определяем степень статической неопределимости заданной системы:

178

Рама имеет две лишние связи и является дважды статически неопределимой.

2. Выбираем основную систему. Отбросим правую опору, имею­щую две связи (два опорных стержня). Основная система — статически определимая консольная рама. Заменим действие отброшен­ных связей двумя силами X_t и Х₂, пока неизвестными (рис. 54, б).

3. Определяем величины изгибающих моментов в характерных точках от заданной нагрузки для основной системы. Стойка BD:

4. Определяем моменты в характерных точках от единичных сил

Стойка BD:

Ригель CD:

Стойка АС:

По найденным значениям строим эпюру Л/, (рис. 54, г); б) от силы Х₂ = 1.

Стойка BD:

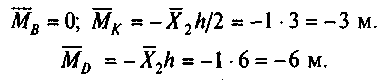
Ригель CD:

Стойка А С:

По найденным значениям строим эпюру М₂ (рис. 54, д). 5. Составляем канонические уравнения метода сил:

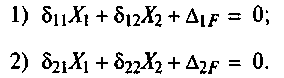
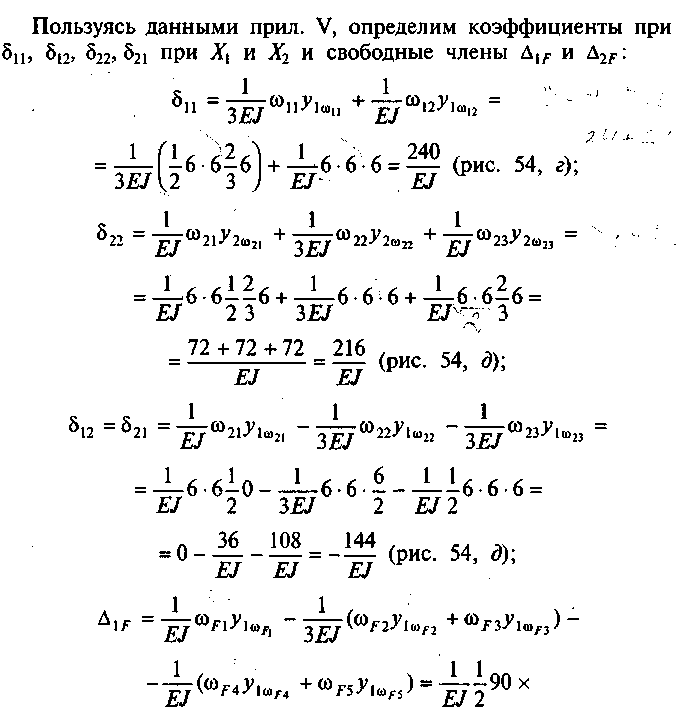
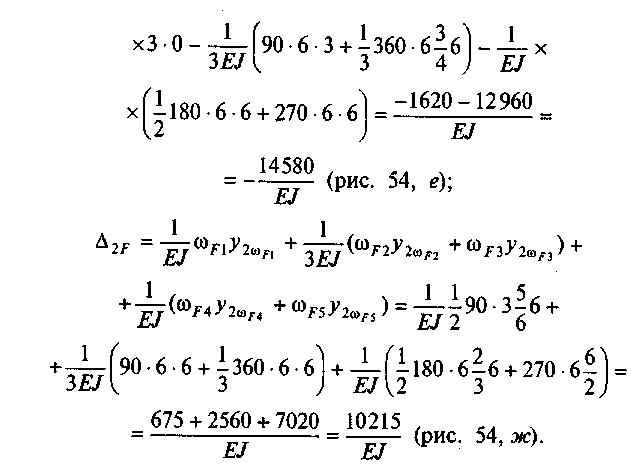
Подставим полученные значения в канонические уравнения:

Решив систему уравнений, получим:

Знак «минус» перед значением силы Х₂ означает, что она в действительности направлена в сторону, противоположную показанной на рис. 54, б.

6. Строим эпюры изгибающих моментов от сил Х_{ и Х₂, равных не единице, а значениям, полученным из решения уравнений:

а) от силы Х_{ = 53,96 кН. Величины моментов от этой силы можно получить умножением значений эпюры М_{ на 53,96 кН:

б) от силы Х₂ - -11,32 кН. Величины моментов от этой силы можно получить умножением значений эпюры М₂ на -11,32 кН:

7. Находим величины изгибающих моментов в характерных точ­ках, суммируя значения моментов эпюр M_F, М_х1 и М_х2 . Стойка BD:

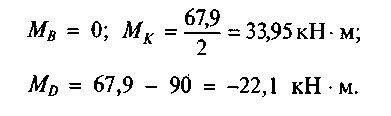
182

Ригель CD:

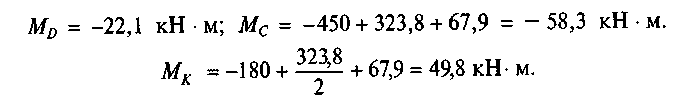
Стойка А С:

По найденным значениям стром эпюру М_х (рис. 54, к). Значе­ния моментов на ригеле между точками Си D должны быть уточ­нены после построения эпюры Q_x или путем использования диф­ференциальных зависимостей между значениями изгибающих моментов и поперечных сил. В данном случае наибольшее значе­ние изгибающего момента на ригеле получается в точке на рас­стоянии 3,3 м от точки С и равно 50,7 кН • м. Такие действия, как построение эпюр Q_x и N_x и выполнение проверки, выходят за рамки задания. Эпюры Q_x и N_x приведены на рис. 54, л, м.

Пример 36. Построить эпюру М_х для рамы, показанной на рис. 55, а.

Решение. 1. Определим степень статической неопределимости заданной системы:

Рама имеет две лишние связи и является дважды статически неопределимой.

2. Выберем основную систему. Отбросим шарнирную опору А, имеющую две связи. Заменим действие отброшенных связей двумя пока неизвестными силами X₁ и Х₂ (рис. 55, б).

3. Определим изгибающие моменты в характерных точках от заданной нагрузки для основной системы. Ригель AD:

Стойка BD:

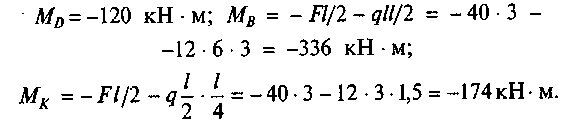
По найденным значениям строим эпюру М_Р (рис. 55, в). 4. Определим значения изгибающих моментов от единичных сил Х_{ и Х₂:

а) от силы Х₁ = 1.

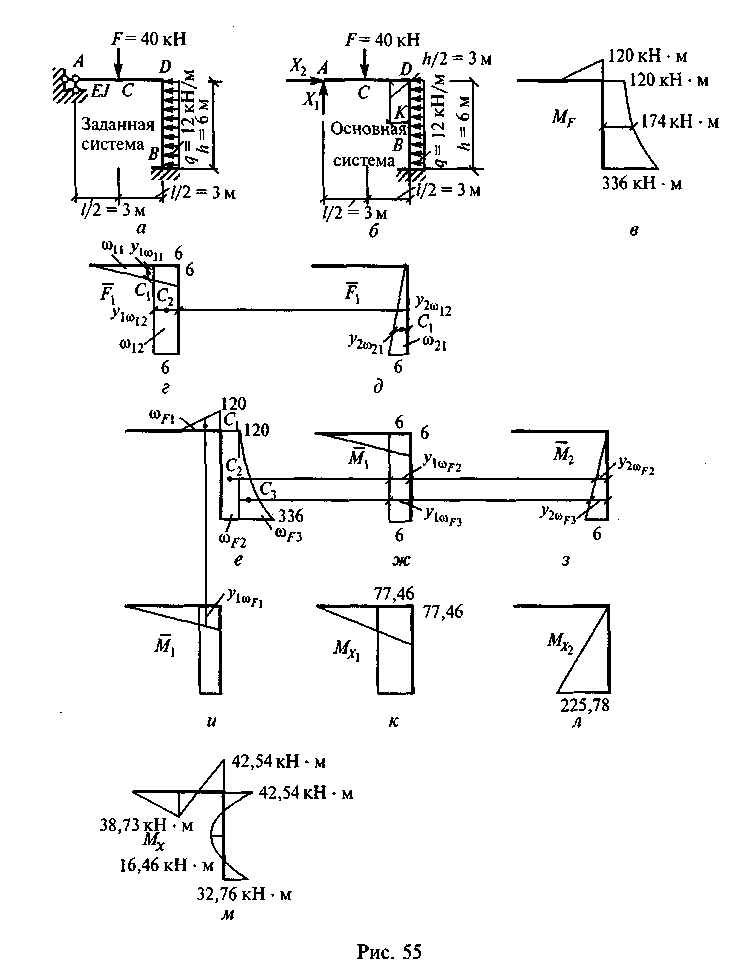
184

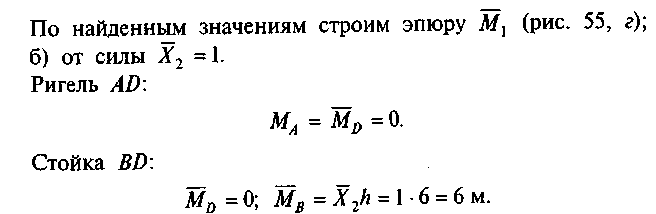
По найденным значениям стром эпюру М₂ (рис. 55, д).

5. Составим канонические уравнения метода сил:

Подставим числовые значения в канонические уравнения

180Х₁ + 54Х₂ - 4356 = 0; 54Х₁ + 16Х₂ - 2052 = 0.

Решив систему уравнений, получим Х₁ = 12,91 кН; Х₂ = 37,63 кН.

6. Строим эпюры изгибающих моментов от сил Х₁ и Х₂;

а) от силы Xi = 12,91 кН. Величины моментов от этой силы получим, умножив значения моментов эпюры М₁ на 12,91 кН:

M_B=M_D =6-12,91=77,46 кН-м (рис. 55, л);

б) от силы Х₂ = 37,63 кН. Величины моментов от этой силы получим, умножив значения моментов эпюры М₂ на 37,63 кН:

М_В = 6 • 37,63 = 225,78 кН-м (рис. 55, м).

7. Определим величины изгибающих моментов в характерных точках заданной системы, суммируя значения изгибающих момен­тов М_f , М_х и М_х в тех же точках.

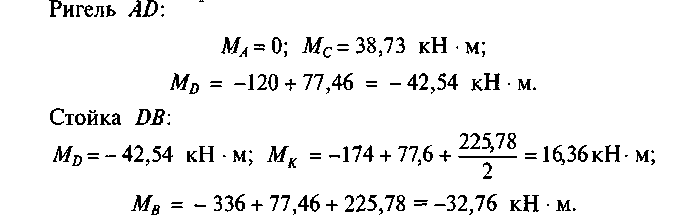
По найденным значениям строим эпюру М_х от заданной нагрузки для заданной системы (рис. 55, н).

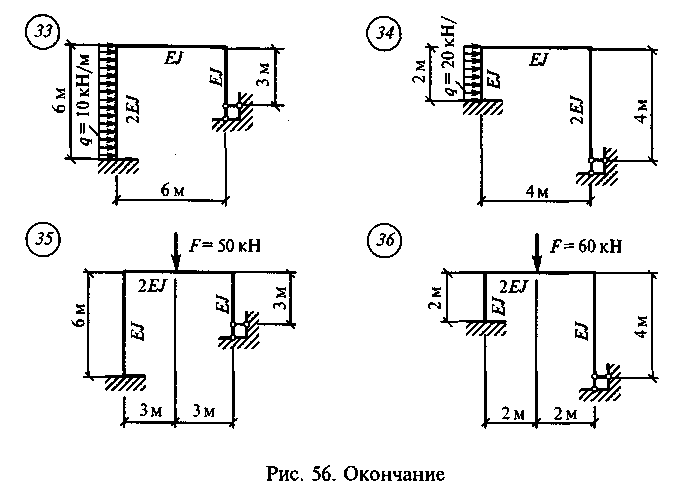
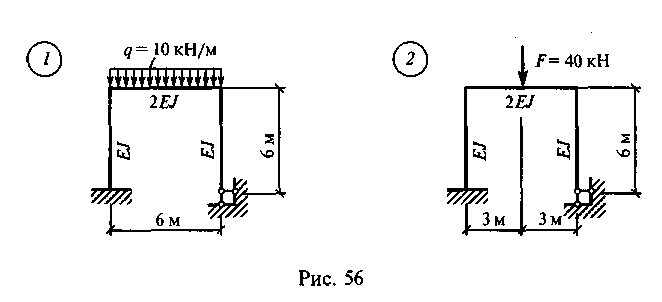
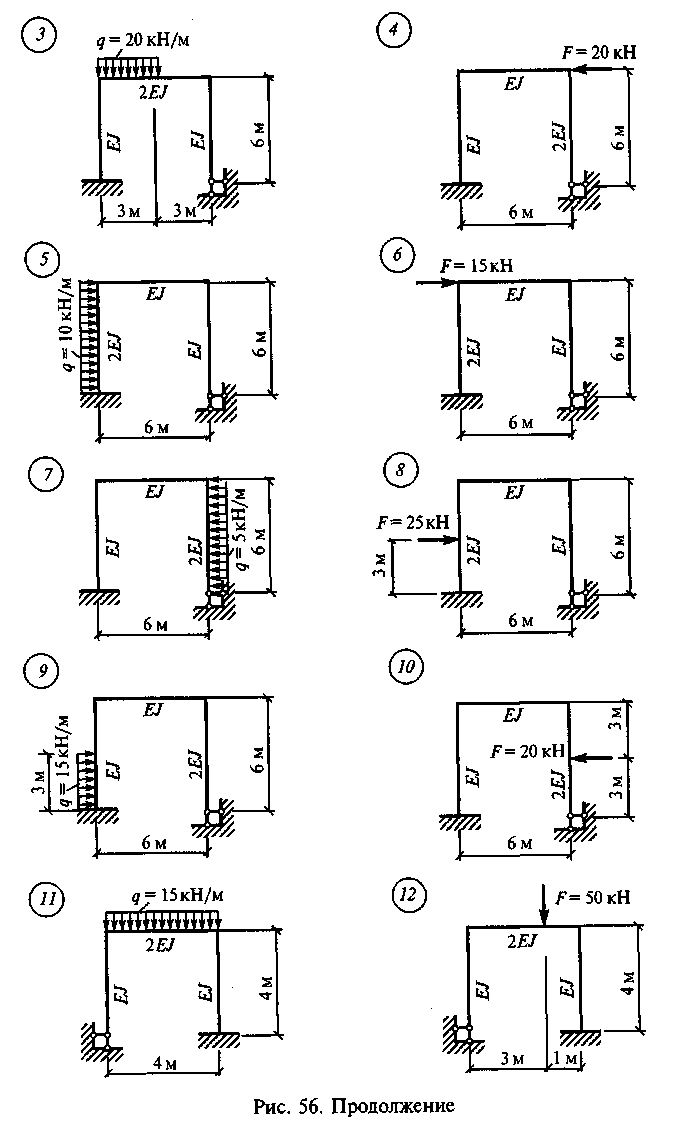
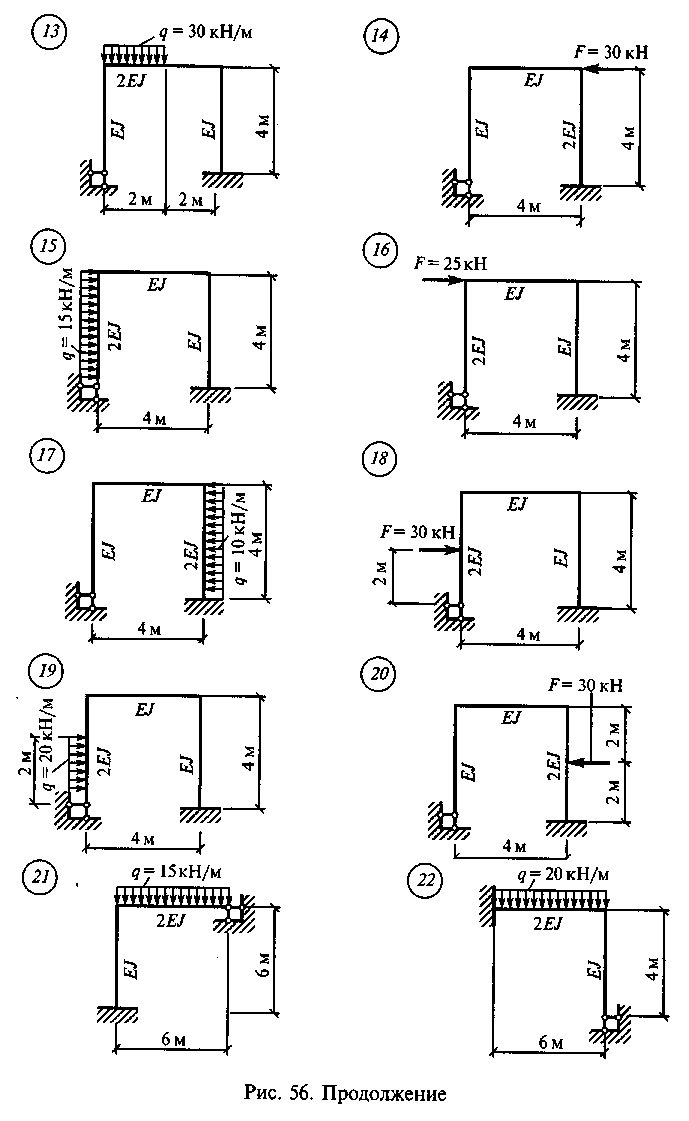
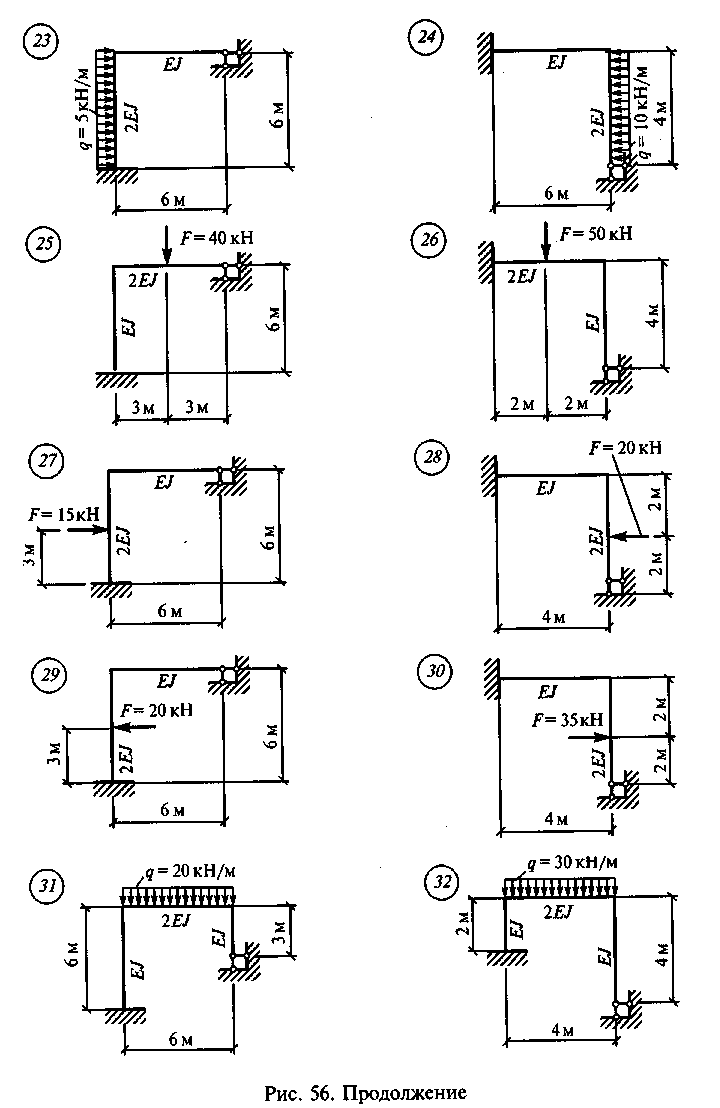
Задание для расчетно-графической работы 10. Построить эпюру М_х для статически неопределимой рамы по данным одного из вариантов, показанных на рис. 56.

186

187

188

189