Глава 6 статика сооружений

6.1. Определение усилий в сечениях трехшарнирной арки

1. Мысленно отбрасывают опоры и заменяют их действие опор­ными реакциями. В опорах трехшарнирной арки возникают четы­ре реакции: две вертикальные V_A, V_B и две горизонтальные Н_А, Н_В, называемые распором.

2. Составляют четыре уравнения равновесия:

из которых определяют четыре неизвестные реакции. Точками А и В обозначены опоры, а точкой С — шарнир.

Правильность определения V_A и V_B может быть уточнена из уравнения

При действии на арку только вертикальных нагрузок горизон­тальные реакции Н_А и Н_В равны между собой и обычно обознача­ются Н.

3. Определяют изгибающие моменты в заданных сечениях арки (арочные изгибающие моменты):

где M_k — арочный изгибающий момент в любой точке арки; М⁰_к — балочный изгибающий момент в том же сечении, т.е. из­гибающий момент в сечении балки, имеющей нагрузки и про­лет, одинаковые с аркой; Н — распор арки; y_k — ордината k-u точки, в которой определяется момент; определяется из уравне­ния оси арки, которое задано в условии задачи.

4. Определяют поперечные силы в заданных сечениях арки:

где Q_k — арочная поперечная сила в любом сечении арки; Q⁰_к — балочная поперечная сила в том же сечении, т.е. поперечная сила в сечении балки, имеющей одинаковую нагрузку и пролет с аркой; ос — угол, образуемый касательной к оси арки в данной точке k; определяется из первой производной уравнения оси арки.

157

5. Определяют продольные силы в заданных сечениях арки:

При определении поперечных и продольных сил на правой половине арки можно рассматривать равновесие левой или пра-вой (какой-то одной) ее части. Если рассматривать равновесие левой части, то:

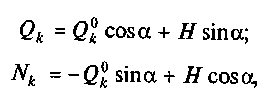
где Q⁰_к — балочная поперечная сила, равная сумме проекций всех левых сил на ось, перпендикулярную оси балки; а — ост­рый угол между касательной и горизонталью; принимается та­ким же, как и для симметричных сечений левой половины арки.

Если рассматривается равновесие правой части арки, то фор­мулы имеют тот же вид, но Q⁰_к принимается равной сумме проек­ций всех правых сил на ось, перпендикулярную оси балки.

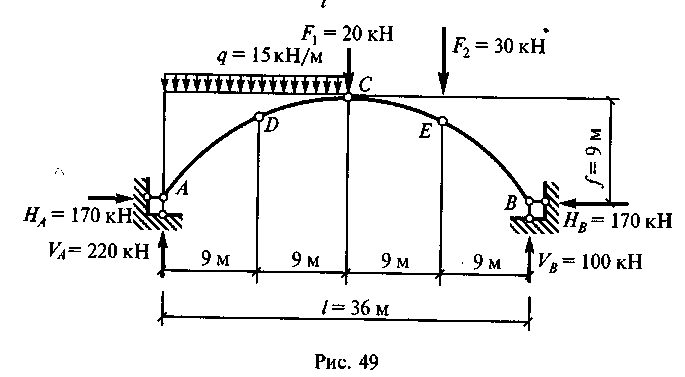
Пример 33. Определить изгибающие моменты, поперечные и продольные силы в точках A, D, С, Е, В (рис. 49) арки параболи­ческого очертания. Уравнение параболы

Первая производная

158

Решение. 1. Обозначим опорные реакции V_A, V_B, H_A и Н_в. 2. Определим опорные реакции по уравнениям равновесия. Первое уравнение

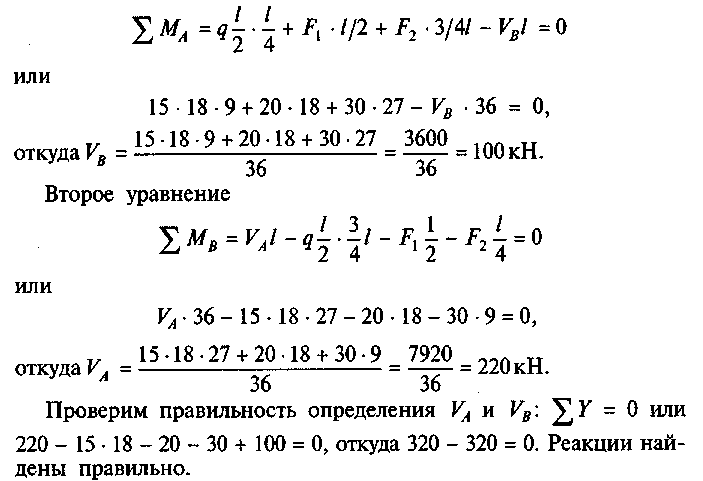
Для составления третьего уравнения можно рассмотреть как левую, так и правую полуарки. Рассмотрим равновесие левой части арки относительно шарнира С:

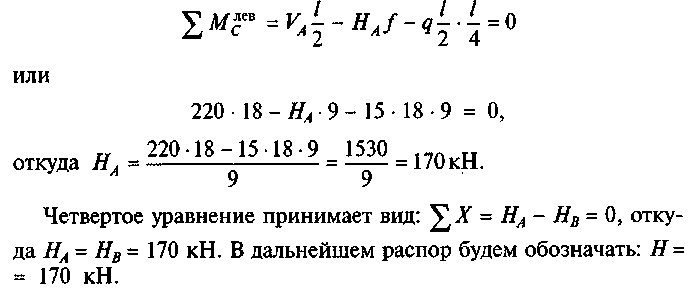
3. Определим изгибающие моменты в точках A, D, С, Е и В по формуле

Определим балочные изгибающие моменты в указанных точ­ках:

159

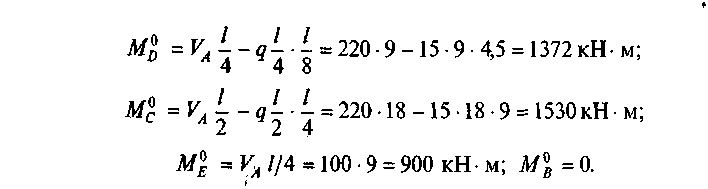
Определим ординаты y_k указанных точек из уравнения пара­болы:

л г

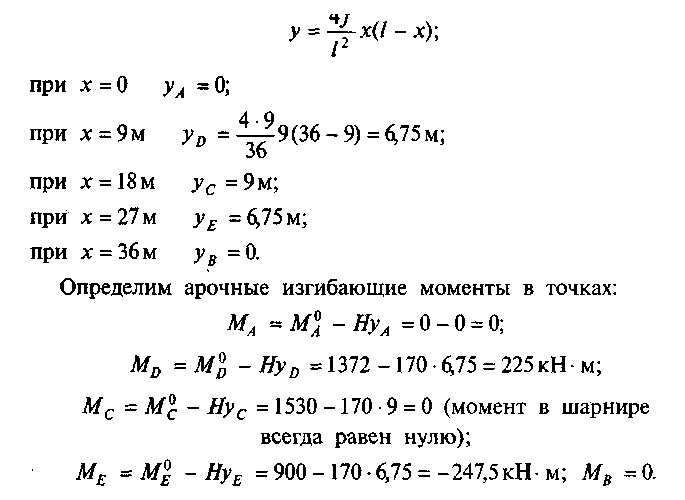
Л. Определим поперечные силы в точках A, D, С, Е и В:

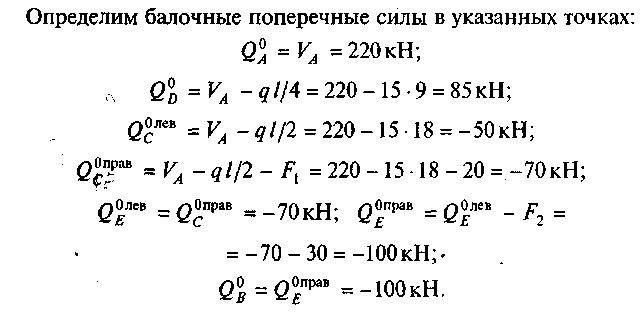
160

Определим углы а для указанных точек. Известно, что

Определим тангенсы углов для указанных точек, сами углы, а также синусы и косинусы углов:

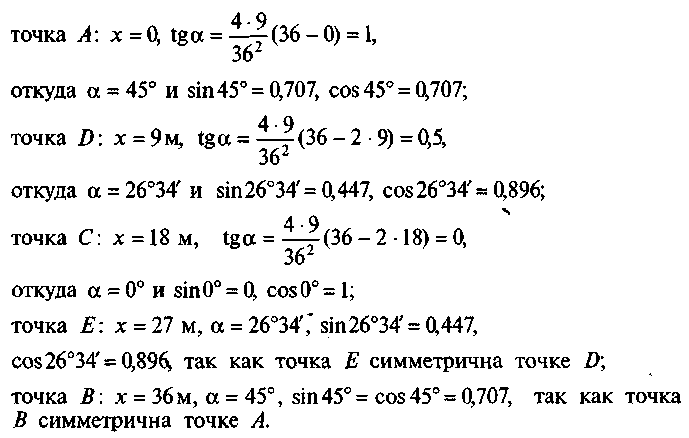
161

В выражениях поперечной силы для сечений правой половины арки знак перед вторым слагаемым изменился на «плюс». 5. Определим продольные силы в точках A, D, С, Е и В:

Подставим числовые значения для каждой точки:

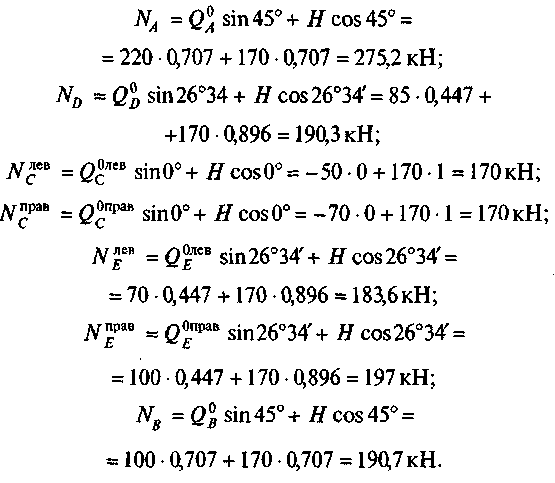
В выражениях продольной силы для сечений правой полови­ны арки знак перед первым слагаемым изменился на «минус».

Если взять большее число точек для определения M_k, Q_k и N _к, например через 1—2 м, то по найденным значениям можно по­строить эпюры изгибающих моментов, поперечных и продоль­ных сил. Это выходит за рамки задания.

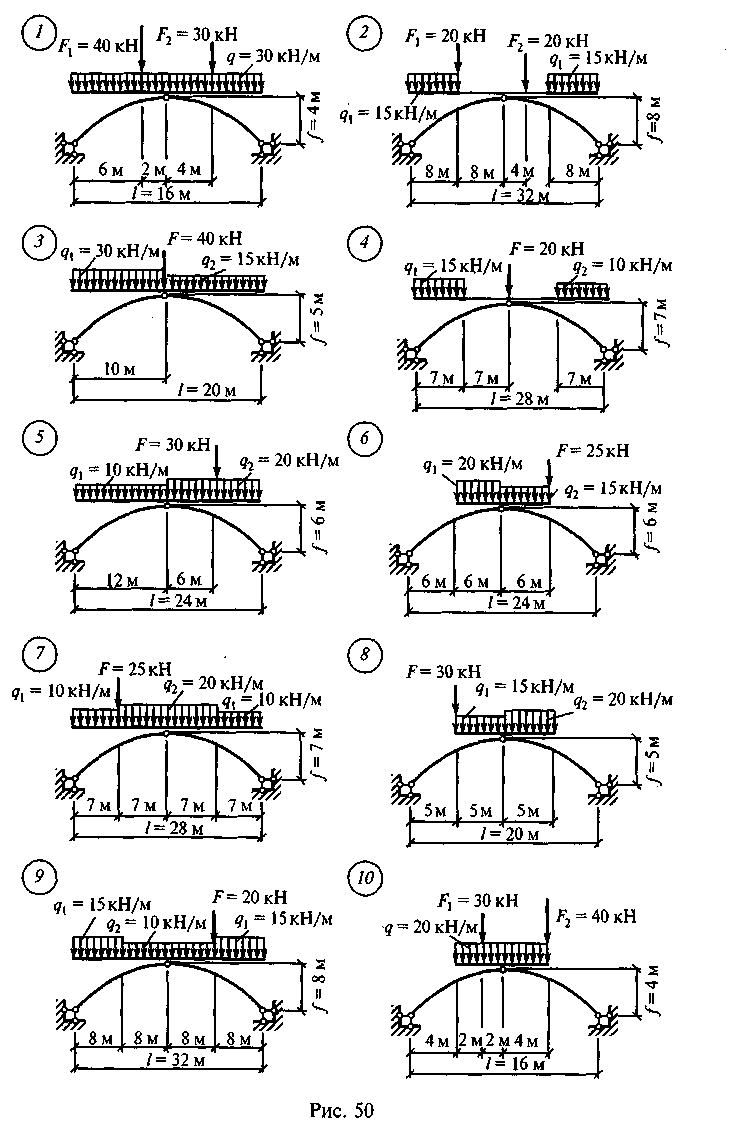
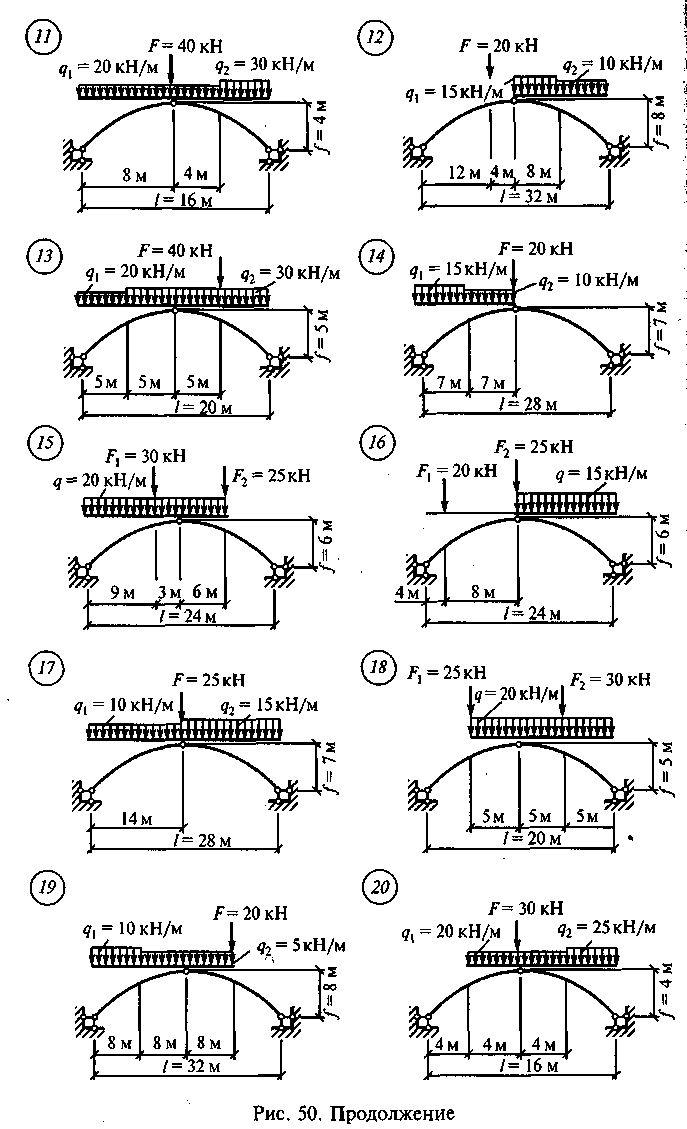
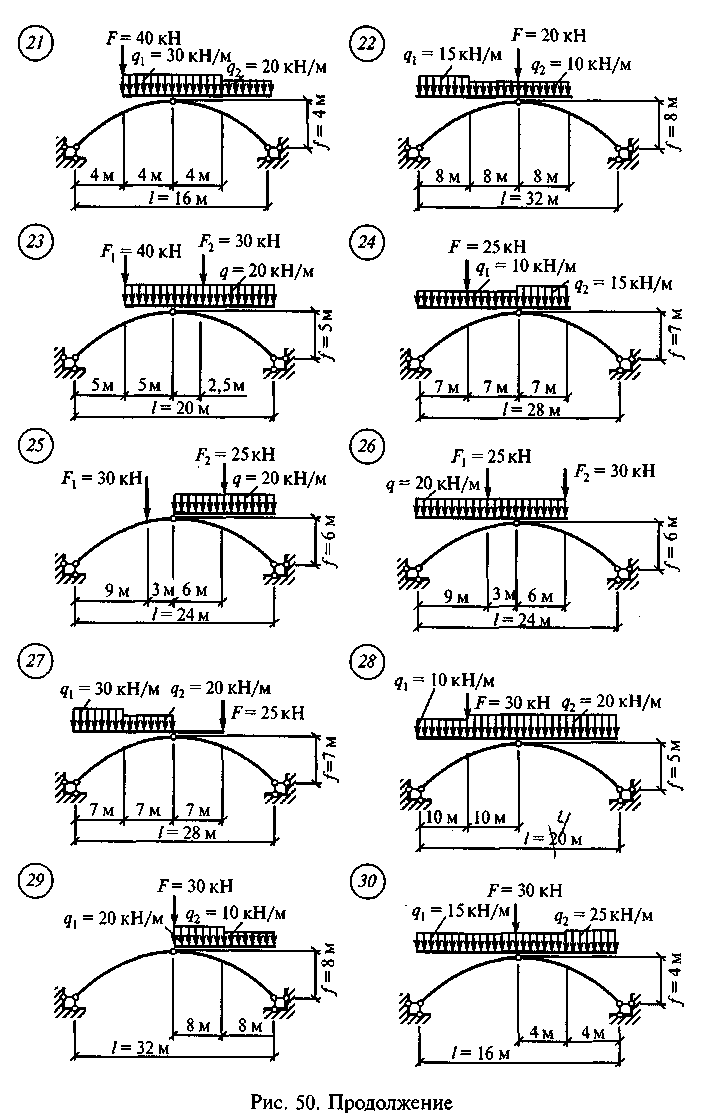
Задание для расчетно-графической работы 8. Определить изгибаю­щие моменты, поперечные и продольные силы в пяти точках: опорах, промежуточном шарнире и серединах., левой и правой полуарки по данным одного из вариантов, показанных на рис. 50. Для нечетных вариантов принять очертание арки параболическим.

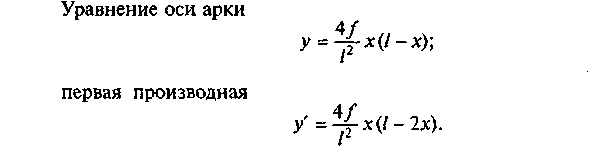
Для четных вариантов принять очертание арки по дуге окружности.

162

163

164

165