5.4. Подбор сечения центрально-сжатой составной стойки

К решению задачи рекомендуется приступить после решения самостоятельной работы 7.

1. Задаются величиной коэффициента продольного изгиба ф. В пер­вом приближении его можно принять равным 0,6...0,8.

2. Определяют требуемую площадь поперечного сечения стойки

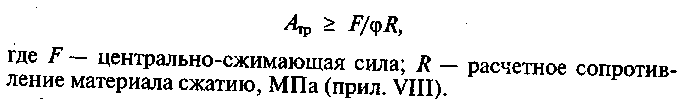
3. По найденной площади определяют номера профилей проката, из которых состоит сечение, используя прил. I. В рамках расчет­ной работы рекомендуется принять профили одинаковыми по площади, если их несколько.

В практических расчетах приходится решать различные зада­чи: обеспечить равную в обеих плоскостях устойчивость стойки или наперед заданное отношение жесткостей (устойчивостей) и т.д. Сложной задачей является выбор типа сечения, его габари­тов, которая довольно сложна и требует специальных знаний, по­этому рекомендации по подбору сечения упрощены.

4. Проверяют устойчивость принятого сечения в следующем порядке:

а) определяют расчетную длину стержня:

148

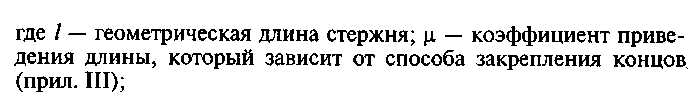
б) определяют моменты инерции сечения J_x и J_y относительно главных центральных осей х и у, которые совпадают с осями симметрии сечения. Моменты инерции профилей проката отно­сительно собственных осей определяются по ГОСТам (прил. I);

в) определяют радиусы инерции сечения относительно осей х и у.

г) определяют гибкость стержня относительно осей х и у:

д) по наибольшему значению Л и в зависимости от материала стойки определяют коэффициент продольного изгиба ф (прил. IV); е) подставляют полученные значения в формулу:

Если это условие удовлетворено, то устойчивость стержня обеспечена, если не удовлетворено — не обеспечена. Если несу­щая способность стойки не обеспечена, то необходимо увеличить площадь сечения, приняв больший профиль, и проверить устой­чивость стойки, добиваясь того, чтобы напряжение было меньше расчетного сопротивления. Если напряжение в стойке равно рас­четному сопротивлению или немного меньше, то сечение счита­ется рационально подобранным, т. е. экономичным. Если напря­жение намного меньше расчетного сопротивления, то такое сече­ние не экономично, так как имеет большой запас прочности. Поэтому, если недонапряжение составляет более 5 %, то следует уменьшить площадь сечения (или увеличить гибкость) стойки, добиваясь, чтобы недонапряжение не превышало 5 %. В некоторых случаях этого не удается добиться из-за ограниченности сорта­мента профилей проката.

Пример 32. Подобрать сечение центрально-сжатой составной стойки, показанной на рис. 47. Материал стойки — сталь С-245.

Решение. 1. Задаемся величиной ф = 0,7.

2. Определим требуемую площадь сечения

149

где R - 240 МПа — расчетное сопротивление стали С-24 (прил. VIII).

Принимаем все профили одинаковыми по площади. На один профиль требуется площадь 50,6 : 3 = 16,8 см². Принимаем два швеллера № 14а площадью А₁ = 1 • 17 = 34 см² и двутавровую балку № 14 площадью А₂ = 17,4 см². Общая площадь сечения

А = 34 +17,4 = 51,4 см²

(см. табл. 3 и 4 прил. I).

3. Проверим устойчивость принятого сечения стержня в следующем порядке:

а) определим расчетную длину стержня

где -ц = 1 для стержня с шарнирным закреплением концов (прил. III);

б) определим момент инерции сечения относительно оси х:

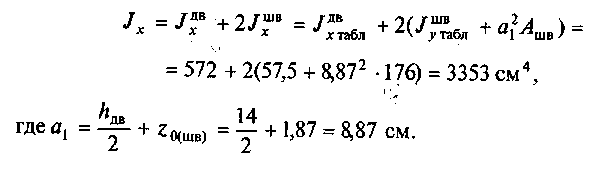
150

Определим момент инерции сечения относительно оси у:

в) определим радиусы инерции сечения

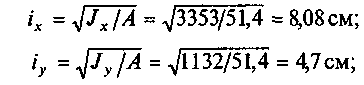
г) определим гибкость стержня относительно осей х и у:

д) для наибольшего значения гибкости Х_у = 85,1 определим ко­эффициент ф (см. прил. IV) по интерполяции между значениями

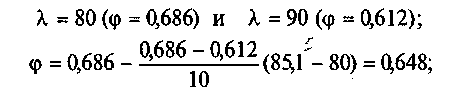
е) определим расчетное напряжение в сечении

Это недопустимо, поэтому необходим перерасчет.

1. Принимаем во втором приближении среднее значение меж­ду тем, которым задались, и тем, что получили:

2. Требуемая площадь сечения

На один профиль требуется 51,6 : 3 = 17,2 см². Принимаем два швеллера № 16 с А_{ = 2 • 18,1 = 36,2 см² и двутавровую балку № 14 с А₂ = 17,4 см². Полная площадь сечения

А = 2-18,1 + 17,4 + 53,6 см².

3. Проверим устойчивость стойки:

а) /о = 4 м, осталось прежним;

б) поскольку J_x > J_y, определим наименьший момент инерции, который дает наибольшую гибкость:

151

в) радиус инерции

г) гибкость стержня

д) коэффициент продольного изгиба получим интерполяцией между

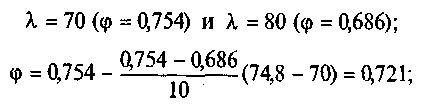
е) расчетное напряжение

ж) недонапряжение равно

что допустимо, но нежелательно.

Выполним перерасчет, уменьшив номера профилей и, как правило, площадь поперечного сечения.

Возможны такие варианты сечения: двутавровая балка № 16 и два швеллера № 14 (А = 51,4 см²); двутавровая балка № 16 и два швеллера № 14 а (А = 54,2 см²). В первом случае напряжение а = = 268,4 МПа, во втором о =243,5 МПа. Решение необходимо провести самостоятельно по приведенной ранее схеме. В обоих случаях напряжения получились больше расчетного сопротивле­ния R = 240 МПа, что недопустимо.

Нам не удалось добиться того, чтобы недонапряжение стало меньше 5 %, поэтому оставляем сечение из двутавровой балки № 14 и двух швеллеров № 16 (А = 53,6 см² и R = 219,9 МПа).

Интересно отметить, что при площади сечения А = 53,6 см² стойка недонапряжена на 8,37 %, а при площади сечения А = = 54,2 см² перенапряжена на 1,4 %, т.е. при меньшей площади стойка обладает большей устойчивостью (жесткостью). Такое явление происходит потому, что кроме площади сечения на ус­тойчивость стойки влияют другие геометрические характери­стики.

Ответ: принято сечение стойки из двух швеллеров № 16 и двутавровой балки № 14.

152

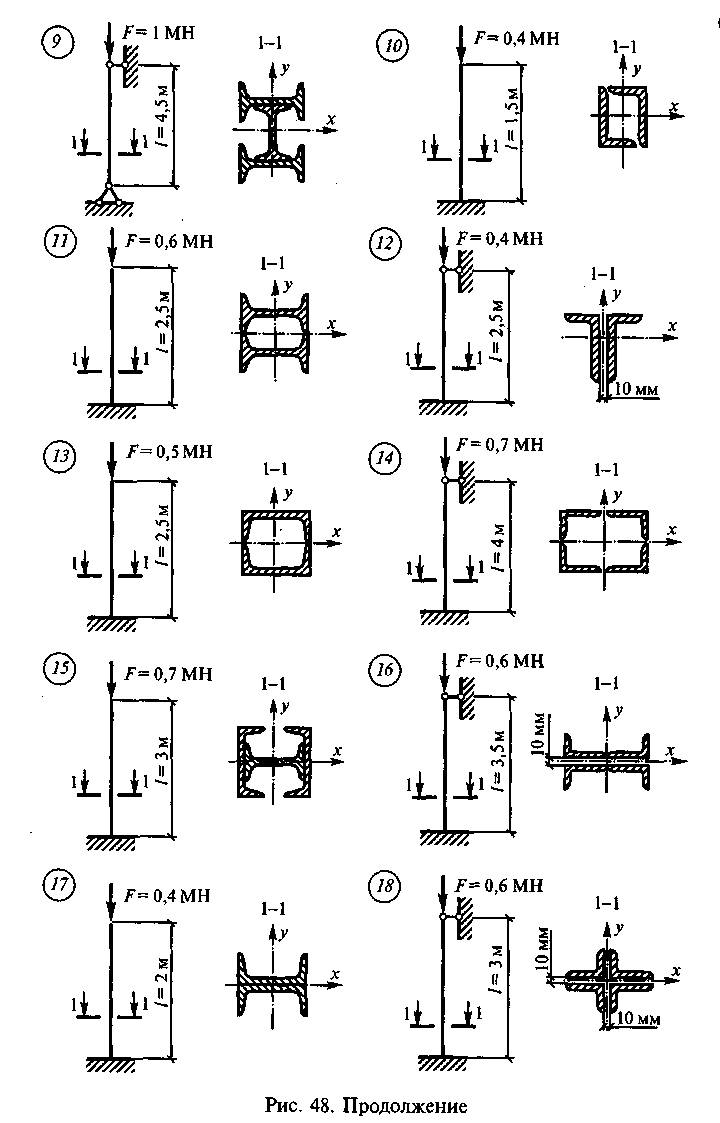
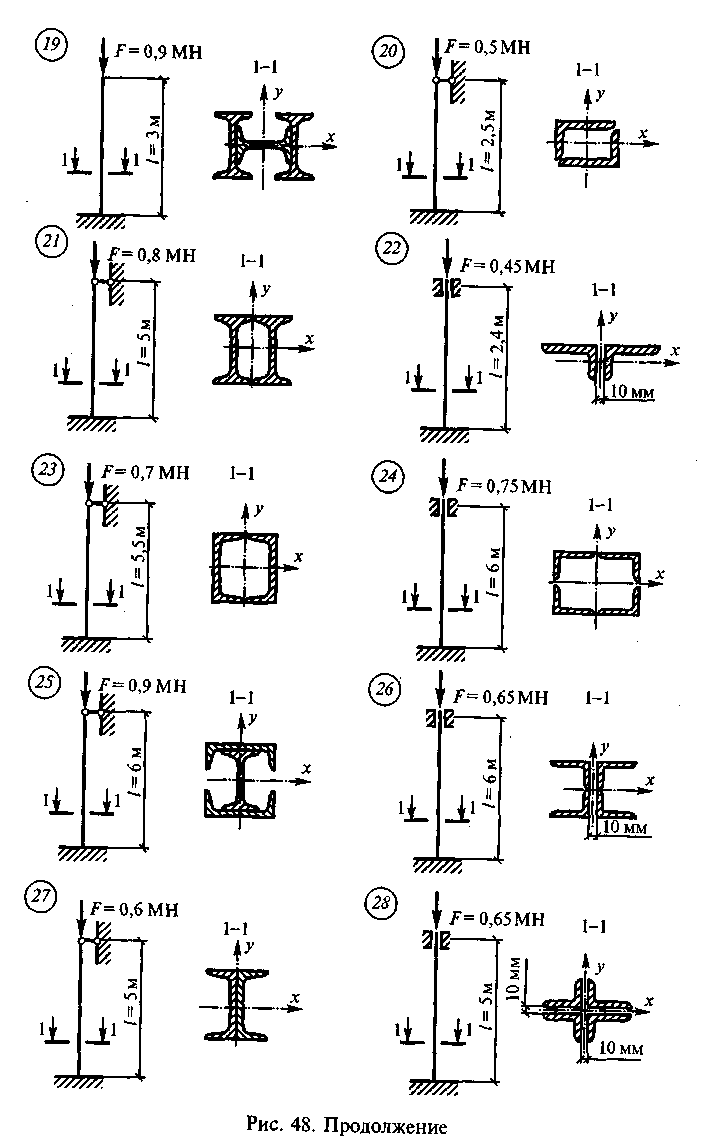
Задание для расчетно-графической работы 7. Подобрать сечение центрально-сжатой стойки по данным одного из вариантов, показан­ных на рис. 48. Материал стойки для нечетных вариантов — сталь С-245, для четных вариантов — сталь С-345.

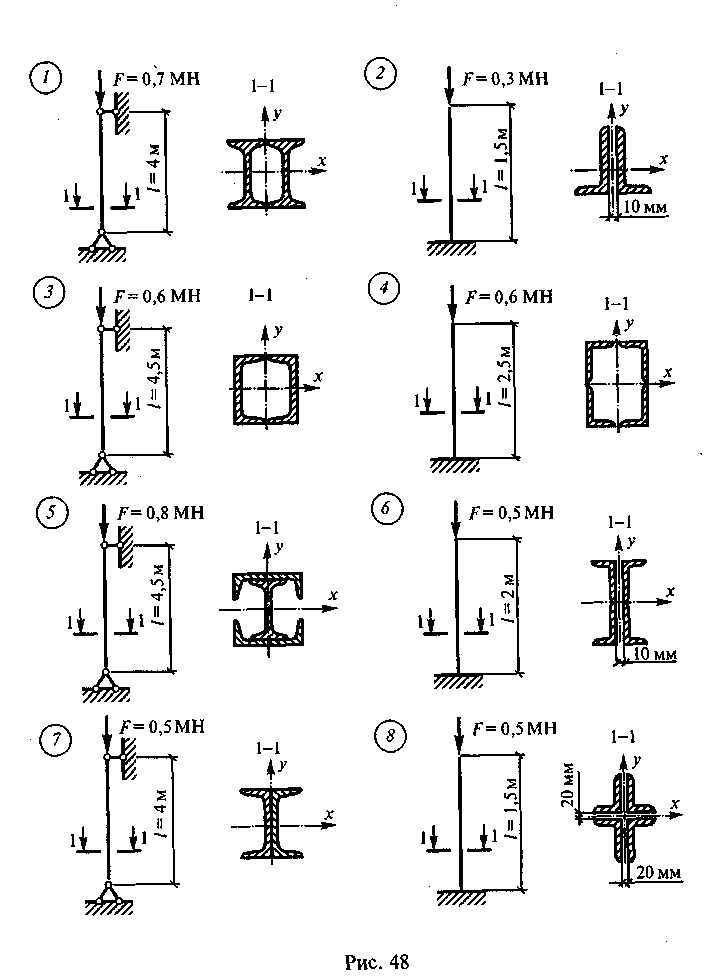
153

154

155