5.1. Определение усилий в стержнях статически

неопределимой системы '

1. Мысленно отбрасывают стержни и заменяют их усилиями в стержнях. Усилия обозначают N₁ и N₂.

2. Устанавливают степень статической неопределимости сис­темы. Под действием нагрузки или других воздействий в системе возникнут три неизвестных: V_A, N₁ и N₂

Для системы параллельных сил можно составить два незави­симых уравнения равновесия, например уравнение моментов от­носительно точек А и В. Таким образом, при трех неизвестных имеем два уравнения. Для решения не хватает одного уравнения. Такая задача называется один раз статически неопределимой. По условию задачи не требуется определения реакции V_A неподвиж­ной опоры А, поэтому из решения следует исключить уравнение, в которое войдет эта реакция. Таким образом, остается одно уравнение моментов относительно неподвижной опоры, которое содержит два неизвестных. Составление уравнения равновесия называется статической стороной задачи.

3. Устанавливают зависимость между деформациями стержней. Для этого вычерчивают деформированную схему системы, в ко­торой показывают систему до и после деформации. На схеме по­казывают удлинения (укорочения) каждого стержня, между кото­рыми всегда можно установить зависимость, рассматривая, на­пример подобие треугольников. Выраженная некоторой форму­лой, она называется уравнением совместности деформации сис­темы. Полученная зависимость между деформациями представ­ляет собой геометрическую сторону задачи.

4. Выражают удлинения (укорочения) стержней в уравнении со­вместности деформации через усилия в этих стержнях. Для этого используют закон Гука:

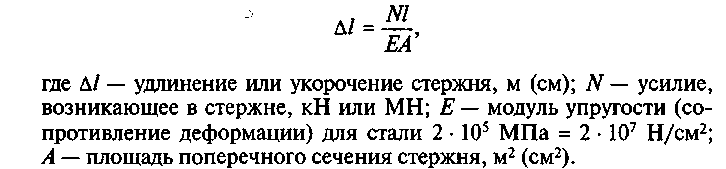
В результате такой подстановки получают еще одну зависи­мость между усилиями N₁ и N₂. Она является недостающим урав-

130

нением к уравнению статики. Полученная зависимость от­ражает физическую сторону за­дачи.

По двум уравнениям опре­деляют неизвестные усилия.

Пример 26. Определить усилия в стержнях ВС и DK, поддерживающих брус AG, как показано на рис. 40, а.

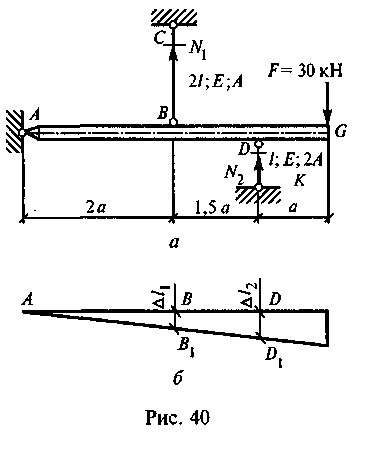
Решение. 1. Отбросим стерж­ни и заменим их усилиями TV, nN₂.

2. Статическая сторона за­дачи. Составим уравнение рав­новесия статики:

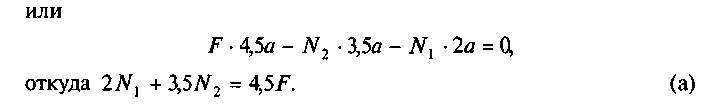
Задача один раз статически неопределима.

3. Геометрическая сторона задачи. Изобразим деформирован­ную схему системы (рис. 40, б). Поскольку брус абсолютно жест­кий, он не деформируется, а только поворачивается относитель­но точки А. Из подобия треугольников АВВ₁ и ADD_} видно, что

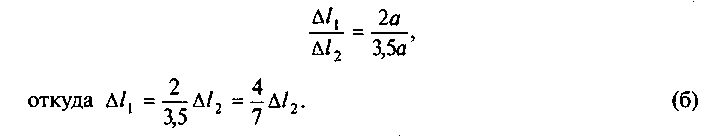
4. Физическая сторона задачи. Выразим деформации стержней уравнения (б) с помощью закона Гука:

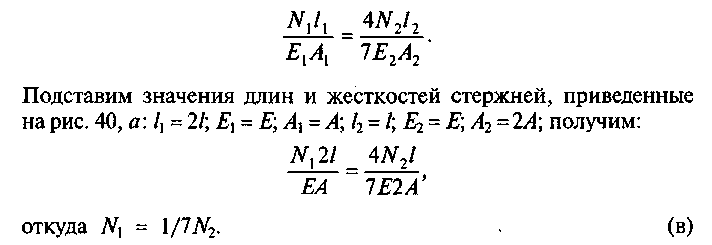
131

Подставим уравнение (в) в уравнение (а):

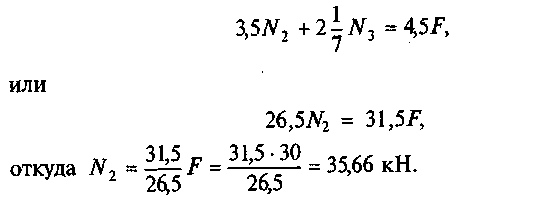
Из уравнения (в) найдем значение второго усилия:

Ответ: n₁ = 5,09 кН; N₂ = 35,66 кН.

Пример 27. Определить усилия в стержнях ВС и DK (рис. 41, j а), поддерживающих брус DA, если стержень DK изготовлен ко-роче проектной длины на a/₀ = 0,001/. Материал — сталь, Е = = 2 • 10⁵ МПа, А = 5 см².

Решение. 1. Обозначим усилия в стержнях N₁ и N₂.

2. Статическая сторона задачи-Составим уравнение равнове­сия:

3. Геометрическая сторона задачи. Покажем деформированную схему системы (рис. 41, б). Если бы не было стержня ВС, то брус AD занял бы положение АП_Ъ т. е. точка D переместилась в положение D₂, причем DD₂ = a/₀. Однако стержень ВС уменьшает величину этого перемещения, и точка D займет какое-то проме­жуточное положение, например D_1, а точка В — положение В\.

Из подобия треугольников АВВ₁ и ADD₁ находим

132

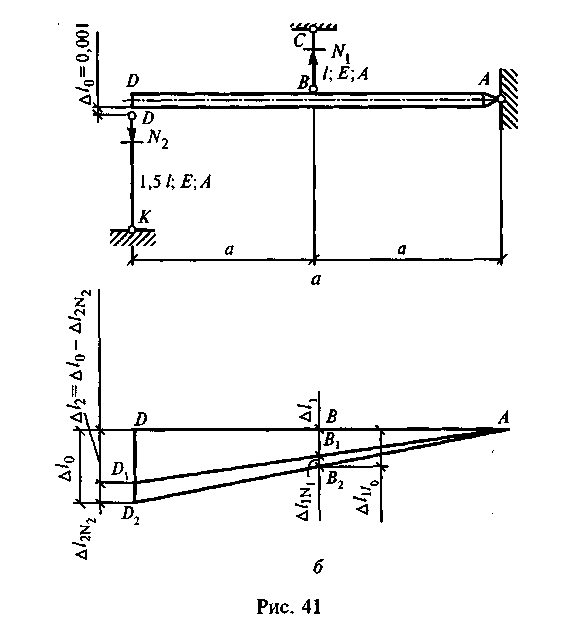
Подставим эти выражения в уравнение (б):

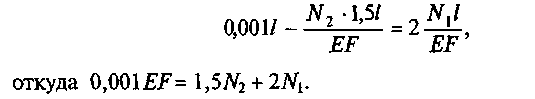
Учитывая уравнение (а)

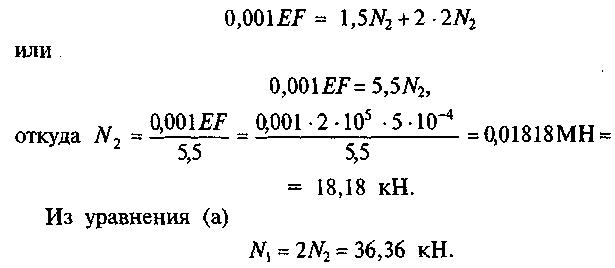
Ответ: N₁ = 36,36 кН; N₂ = 18,18 кН. Оба стержня испытывают растяжение.

133

Пример 28. Определить усилия в стержнях ВС и DK (рис. 42, а), поддерживающих брус AD, если температура стержня ВС увели­чится на 20°С. Материал — сталь, а = = 12 - 10 ^-6; Е = 2 • 10⁵ МПа, площадь сечения А = 5 см².

Решение. 1. Заменяем стержни усилиями в стержнях N₁ и N₂.

2. Статическая сторона задачи. Уравнение равновесия статики:

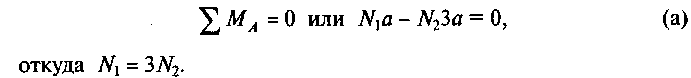
3. Геометрическая сторона задачи. Покажем деформированную схему системы (рис. 42, б). Если бы стержня DK нe было, то точ­ка D, вследствие удлинения стержня ВС от увеличения темпера­туры, переместилась бы в положение D₂. Стержень DK не дает возможности точке D переместиться в положение D₂, и она зай­мет какое-то промежуточное положение D_1, т.е. стержень DK укоротится на величину DD ₁, которую обозначим через a/₂.

Стержень ВС удлинится на величину ВВ ₁ , которую обозна­чим a/₁

134

Из подобия треугольников АВВ₁ и ADD_l

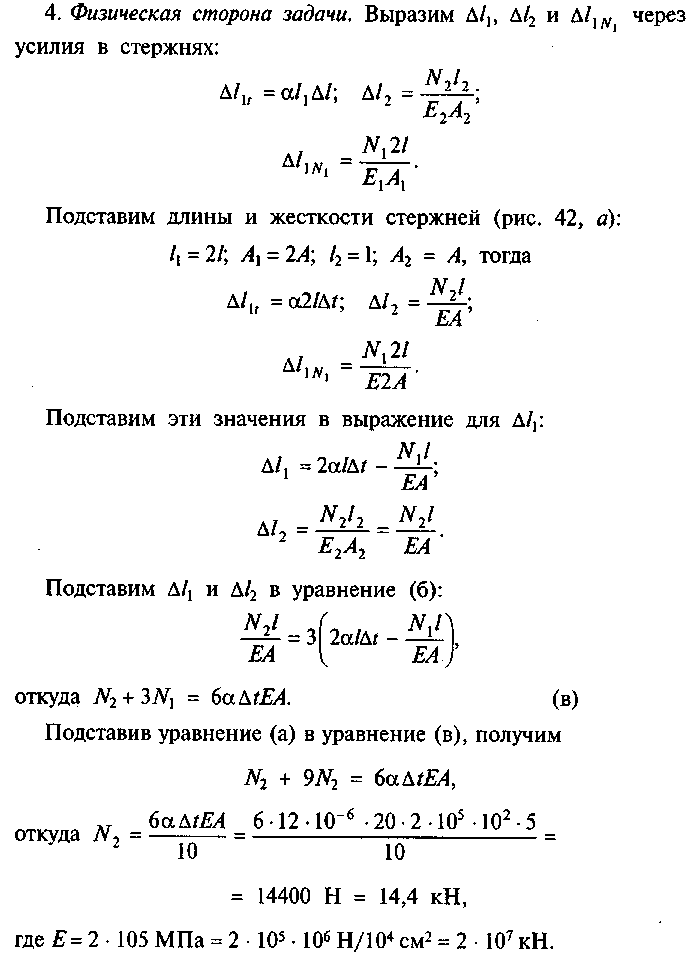
135

136

137

138

Из уравнения (а)

N₁ = 3N₂ = 3 • 14,4 = 43,2 кН.

Ответ: N₁ = 43,2 кН, стержень сжат; N₂ = 14,4 кН, этот стер­жень тоже сжат, так как усилия на рис. 42 направлены к брусу.

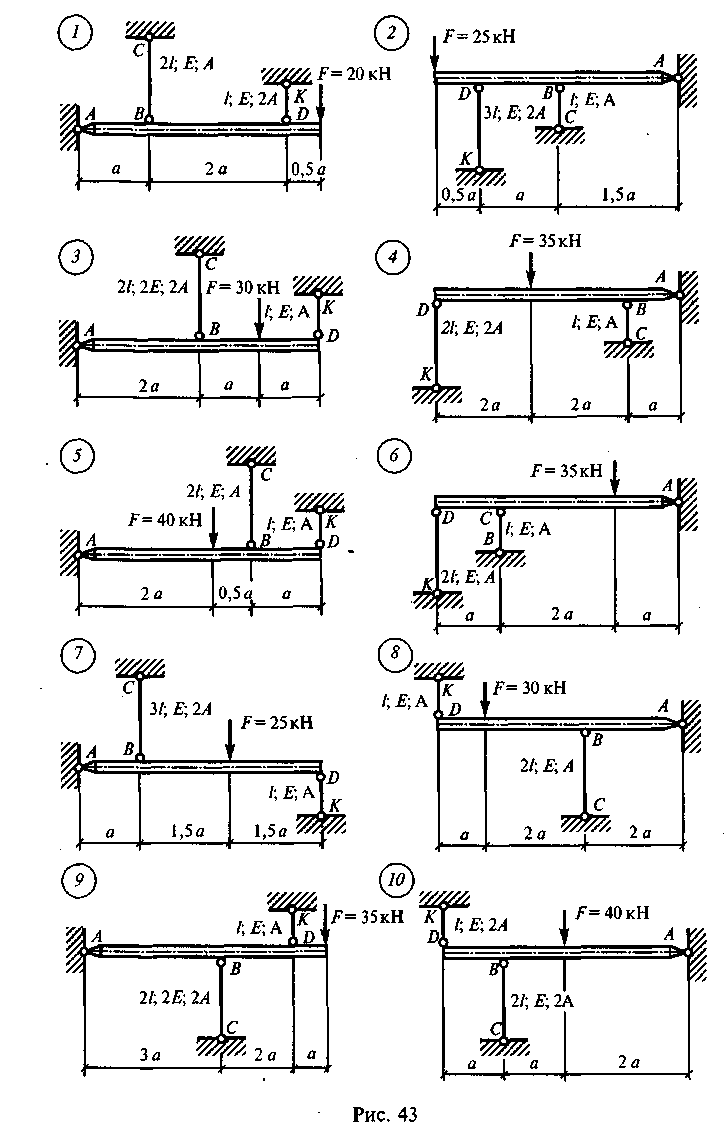
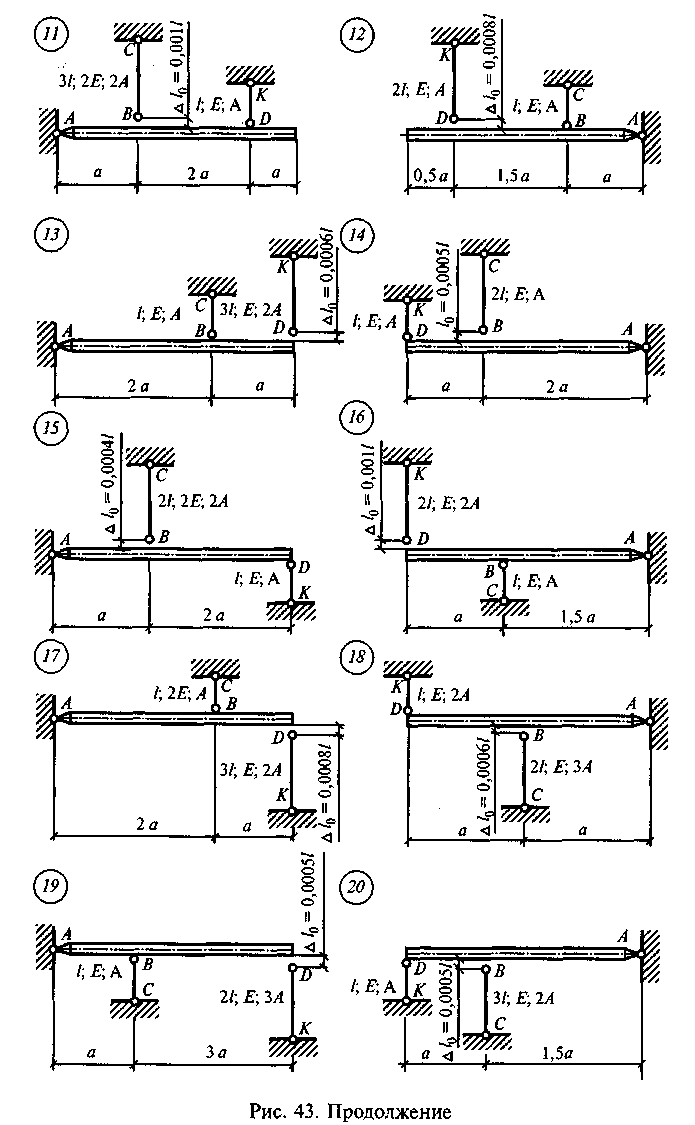
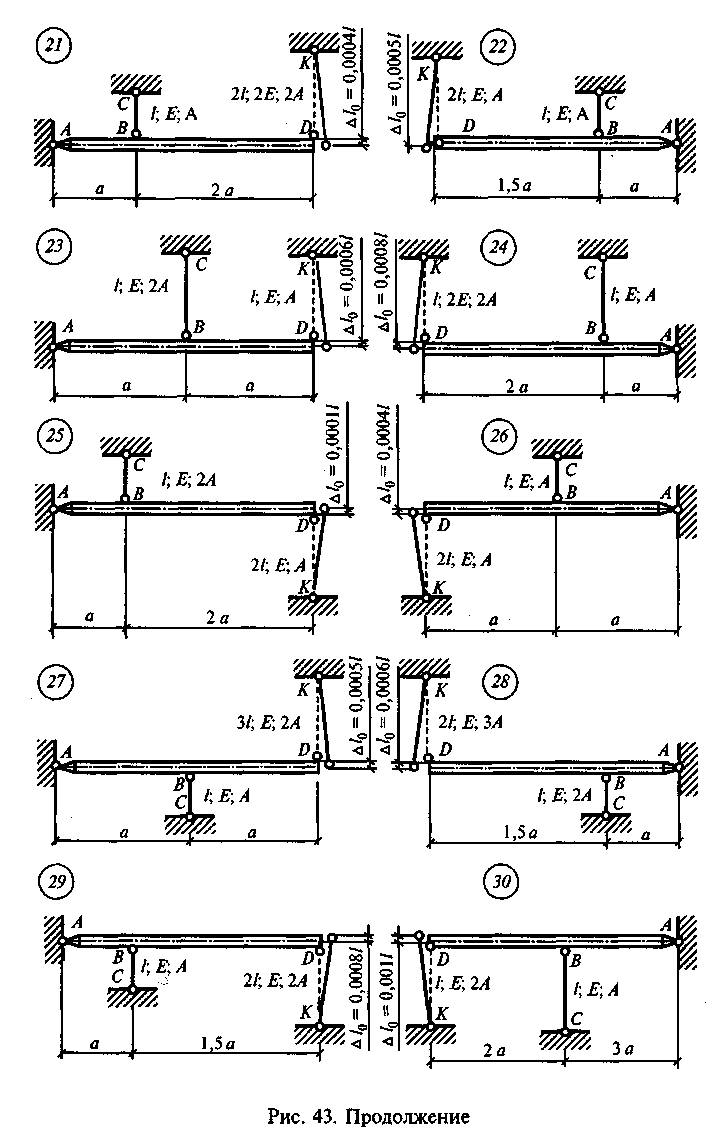
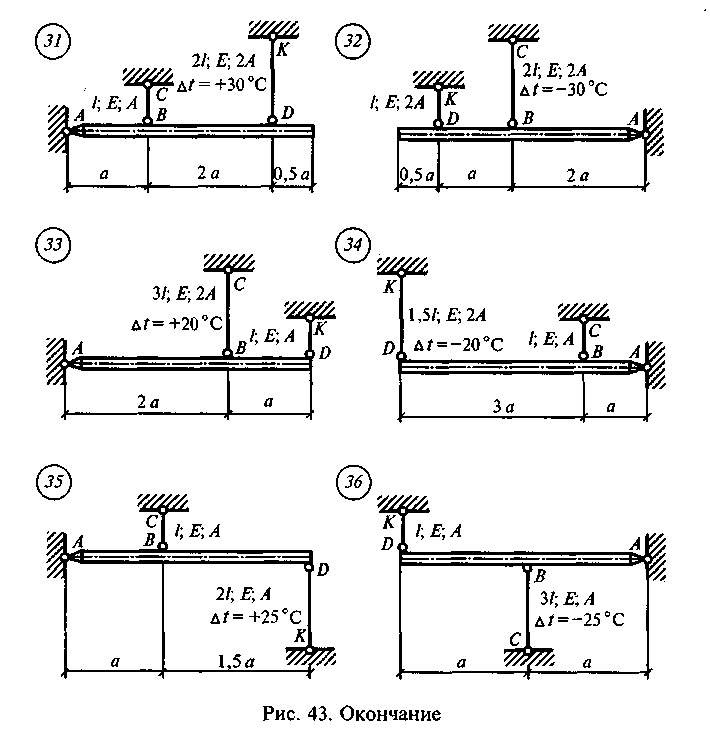
Задание для расчетно-графической работы 4. Определить усилия в стержнях системы, поддерживающей абсолютно жесткий брус, по дан­ным одного из вариантов, показанных на рис. 43: а)в вариантах 1—10 — от силы F;

б) в вариантах 11—20 один из стержней изготовлен короче проект­ной длины на a /₀, материал — сталь, А = 10 см²;

в) в вариантах 21—30 один из стержней изготовлен длиннее про­ектной длины на a/о, материал — сталь, А = 5 см²;

г) в вариантах 31—36 температура одного из стержней увеличилась на at°С, материал — сталь, А =10 см².

139