Раздел II расчетно-графические работы

Глава 4 теоретическая механика. Статика

4.1. Определение усилий в стержнях простейшей консольной фермы

Задачу можно решать аналитическим или графическим спосо­бом.

Аналитическое решение

1. Обозначают узлы и стержни фермы. Узлы можно обозначить буквами, а стержни — цифрами. Порядок обозначения произ­вольный.

2. Определяют величины углов между стержнями в каждом узле, используя геометрическую схему фермы.

3. Мысленно вырезают узел, в котором сходятся два стержня. Определяют усилия в этих стержнях в следующем порядке:

а) стержни заменяют усилиями в них. Усилия принято обозна­чать буквой S с подстрочным индексом, указывающим номер стержня, в котором определяется усилие. Удобнее узел показать на отдельном рисунке, придерживаясь масштаба при изображении углов;

б) выбирают систему осей координат. Начало координат со­вмещают с точкой пересечения всех стержней. Одну из осей со­вмещают с одним из неизвестных усилий, а вторую — проводят перпендикулярно первой. Можно оси располагать традиционно: одну вертикально, другую горизонтально (см. самостоятельную работу 1);

в) составляют уравнения равновесия:

Решают их и находят неизвестные усилия.

4. Вырезают поочередно все узлы фермы, причем каждый выре­занный узел должен иметь не более двух неизвестных усилий. Порядок определения остается таким же, как для первого узла. В задачах расчетной работы требуется рассмотреть 3—4 узла.

101

Графическое решение

1. Вычерчивают геометрическую схему фермы строго в масшта­бе. Масштаб выбирается произвольно и определяется размерами чертежа. Начать можно с масштаба, например, 1:50.

2. Выбирают масштаб сил. Рекомендации по выбору масштаба сил дать трудно. Начать можно с масштаба в 1 см 5 или 10.кН. При неудачной попытке масштаб следует изменить.

3. Мысленно вырезают узел, в котором сходятся два стержня. Определяют усилия в этих стержнях в следующем порядке:

а) обозначают стержни и усилия, как при аналитическом ре­шении;

б) определяют усилия в стержнях первого узла. Для этого в принятом масштабе сил откладывают известную по величине и направлению силу, приложенную в узле. Зате.м через начало и конец вектора, изображающего силу, проводят две линии, парал­лельные стержням, в которых отыскиваются усилия, до взаимно­го их пересечения. Измеренные в масштабе сил отрезки (стороны треугольника) дают величину усилия в стержне, параллельном этому отрезку;

в) определяют знак усилия. Устанавливают направление дей­ствия усилия на силовом треугольнике. Для системы сил, находя­щейся в равновесии, все стрелки в нем должны быть направлены в одну сторону. Направление обхода треугольника определяется направлением действия силы. Перенесем полученное направле­ние усилия на узел. Если при этом усилие направлено к узлу, то стержень будем считать сжатым, а если от узла — растянутым.

4. Рассматривают следующий узел. Это будет узел, в котором сходятся два неизвестных усилия. Сначала откладывают извест­ные по величине и направлению усилия в масштабе сил. Через начало первого и конец последнего усилия проводят линии, па­раллельные стержням, усилия в которых неизвестны, до взаим­ного их пересечения. Полученные стороны многоугольника сил, измеренные в масштабе, представляют собой величины неизвест­ных усилий. Знак усилий определяется по правилам, приведен­ным для первого узла.

Каждым следующим вырезаемым узлом является тот, в кото­ром сходятся не более двух неизвестных усилий. Сравнивают ре­зультаты решения задачи двумя способами: аналитическим и гра­фическим.

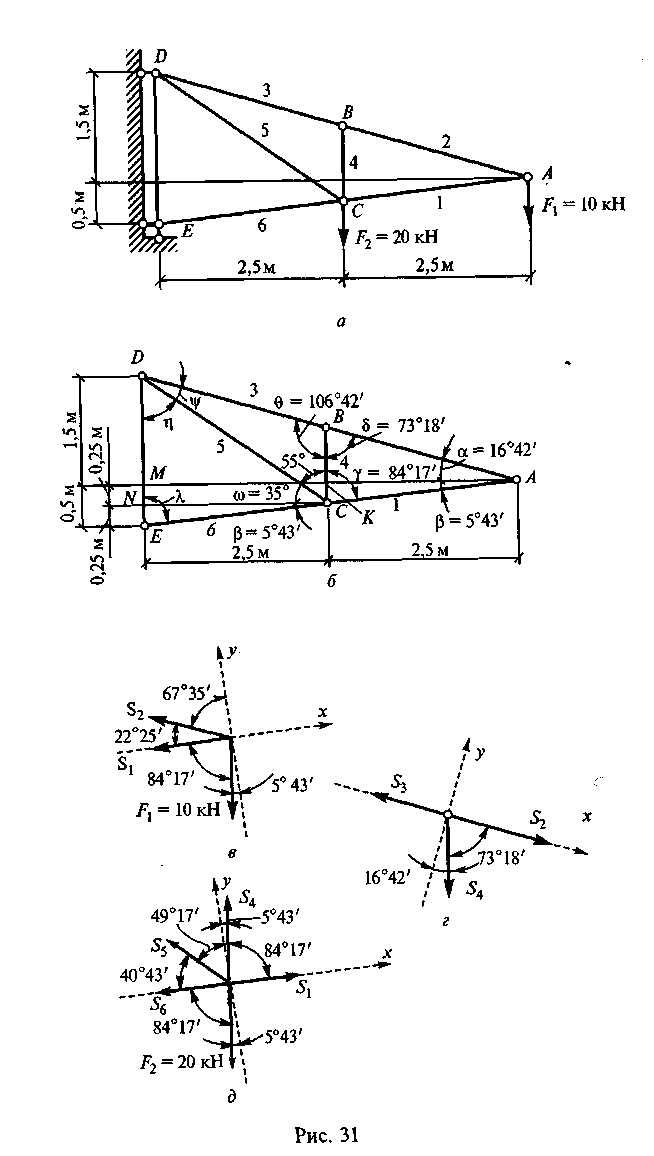
Пример 22. Определить усилия в стержнях консольной фер­мы, показанной на рис. 31, а, аналитическим и графическим способами. Рассмотреть три узла.

Аналитическое решение

1. Обозначим узлы А, В, С, D, Е и стержни 1, 2, 3, 4, 5, 6.

102

2. Определим углы между стержнями в каждом узле (рис. 31, б).

Из треугольника AMD

Из треугольника АМЕ

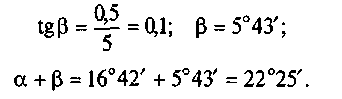
Из треугольника АКБ

Из треугольника АКС

Из треугольника CND

По условию задачи требуется рассмотреть три узла, поэтому углы \|/, т) и А для решения не потребуются.

3. Вырезаем узел А, в котором сходятся два стержня 1 и 2. Оп­ределяем усилия в этих стержнях:

а) заменяем стержни усилиями S₁ и S₂ (рис. 31, в);

б) выбираем систему координат. Ось х совместим с неизвест­ным усилием S₁ , а ось у направим перпендикулярно оси х. Ука­жем углы между усилиями (или соответствующими им стержня­ми) и осями координат;

в) составляем уравнения равновесия:

Первое уравнение для узла А

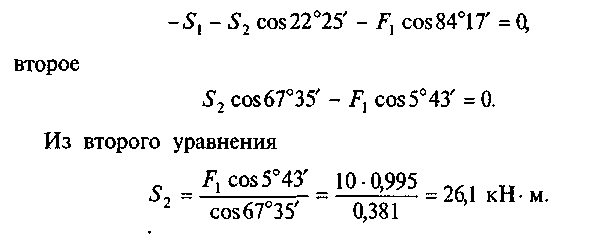
103

104

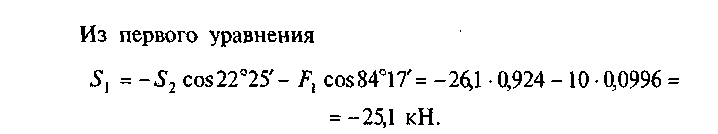
Знак «плюс» свидетельствует о том, что стержень 2 растянут, а «минус» — стержень 1 сжат.

4. Рассмотрим узел В (рис. 31, г). В нем сходятся два стержня 3 и 4, усилия в которых неизвестны. Ось х совместим с неизвест­ным усилием 5₃. Составим уравнения равновесия:

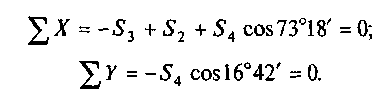
Из второго уравнения видно, что S₄ = 0, так как cos 16°42' не может быть равен нулю. С правилами определения стержней, усилия в которых равны нулю (нулевые стержни), без составле­ния уравнений можно ознакомиться в работе [4, с. 345]. Из пер­вого уравнения

5. Рассмотрим узел С. В нем сходятся стержни 5 и 6, усилия в которых неизвестны. Ось х совместим с неизвестным усилием S₆ и укажем углы между усилиями и осями координат (рис. 31, д). Составим уравнения равновесия. Уравнения для узла С примут вид:

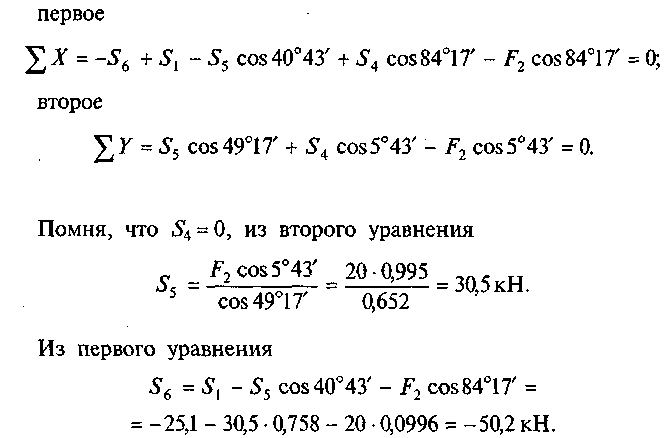
105

Графическое решение

1. Вычерчиваем ферму в масштабе, например 1:50 (рис. 32, а).

2. Выбираем масштаб сил, например в 1 см 10 кН.

3. Мысленно вырезаем узел А. Определим усилия в стержнях 1

и 2:

а) обозначим усилия в стержнях 5_г и S₂',

б) из произвольной точки а проводим отрезок ab, параллель­ный и равный в принятом масштабе силе /,. Через точки а и Ъ проводим линии, параллельные стержням 1 и 2 до взаимного пе­ресечения (рис. 32, б). Полученные отрезки be и ас, измеренные

106

в масштабе сил, соответствуют усилиям S_t и S₂ в стержнях 1 и 2. Длина отрезка be - 2,5 см, следовательно, S_} - 2,5 • 10 = 25 кН. Длина отрезка ас = 2,6 см, S₂ = 2,6-10 = 26 кН;

в) определим знаки усилий. Направление силы f, известно — она направлена вниз. Поставим стрелки на отрезках be и са так, чтобы они были направлены в одну сторону. Перенесем направ­ление усилия 5, на стержень 1 (см. рис. 32, а), оно направлено к узлу, т.е. стержень 1 сжат. Усилие S₂ при таком переносе направ­лено от узла, т.е. стержень 2 растянут.

4. Вырезаем узел В. Из точки d (рис. 32, в) проведем известное усилие S₂. Через концы отрезка (точки d u e) проводим линии, параллельные стержням 3 и 4. Из построения следует, что £₄ = О, а S ₃= S₂ = 26 кН.

5. Вырезаем узел С. Проведем линии, параллельные уже из­вестным усилию S_{ и силе F₂ в принятом масштабе (рис. 32, г). Через точки k и п проводим линии, параллельные стержням 5 и 6, до их пересечения в точке т. Отрезки km и тп, измеренные в масштабе сил, дают величины усилий S_s - 3,05 • 10 = = 30,5 кН и S₆ - 5 • 10 = 50 кН. Определим знаки усилий. Все стрелки на си­ловом многоугольнике nf km расставим против часовой стрелки. Это определено направлением усилия S_} и силы F₂. Перенесем направление усилия S₅ на стержень 5 в узле С; оно будет на­правлено от узла, т. е. стержень 5 растянут. Перенесем направле­ние усилия 5₆ на узел С, оно будет направлено к узлу, т. е. стер­жень 6 сжат.

Составим сравнительную таблицу усилий, найденных анали­тическим и графическим способами (табл. 2).

Очевидно, что аналитический способ более точен.

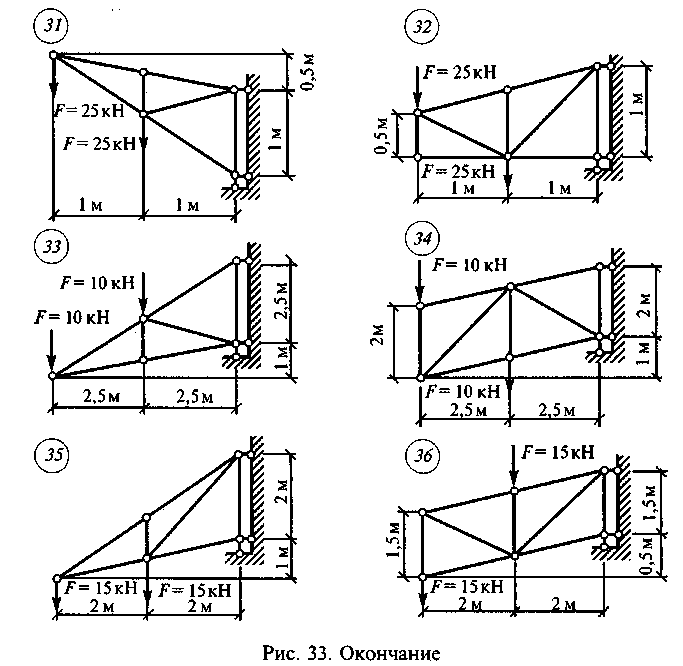
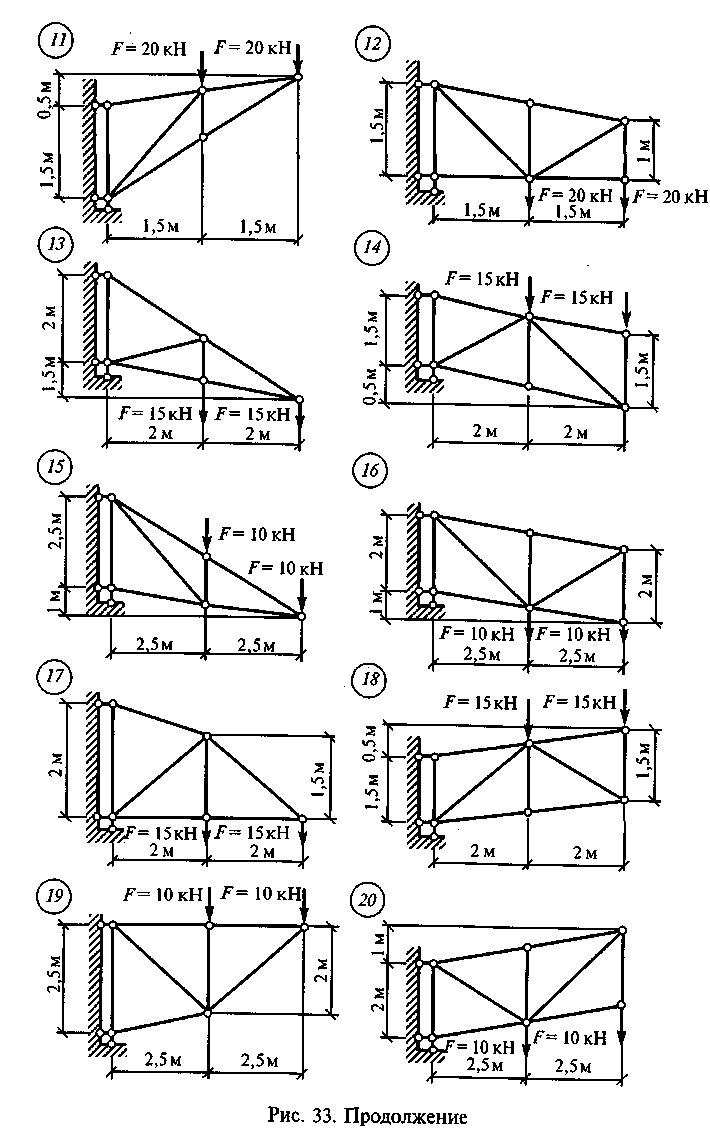
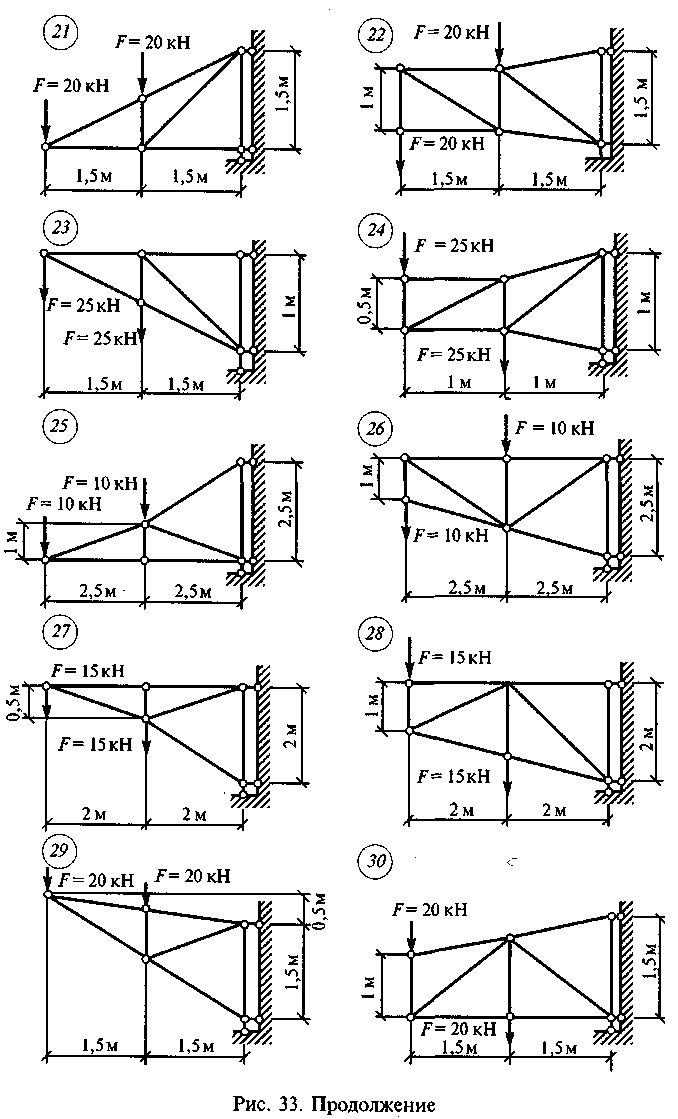
Задание для расчетно-графической работы 1. Определить усилия в стержнях консольной фермы аналитическим и графическим способами по данным одного из вариантов, приведенных на рис. 33. В заданиях с нечетными вариантами рассмотреть три узла, а с четными — четыре, начиная от свободного конца.

107

108

109

по