3.3. Определение линейных перемещений в простейших консольных рамах

1. Строят эпюру M_F изгибающих моментов от заданной нагруз­ки. В задачах для самостоятельной работы приведены консоль­ные рамы (или брусья с ломаной осью). Эпюра M_F для такой

80

рамы может быть построена без определения опорных реакций. Для этого необходимо начинать определение изгибающих мо­ментов от свободного (незаделанного) конца. Эпюра строится со стороны растянутого волокна.

2. Разбивают эпюру M_F на простые геометрические фигуры. треугольники и прямоугольники. Определяют площади фигур и положение их центров тяжести.

3. Указывают какую-либо точку, перемещение которой требу­ется определить. По условию задачи требуется найти вертикаль­ное или горизонтальное перемещение какой-либо точки рамы. По тем же данным может быть решена задача определения угла поворота какого-либо сечения рамы.

Прикладывают силу F - 1 (единичнуюсилу) по направлению искомого линейного перемещения или М -1 (единичного мо­мента) по направлению искомого углового перемещения. В зада­чах самостоятельной работы отыскиваются только линейные пе­ремещения.

_ 4. Строят эпюру изгибающих моментов от единичной силы F = 1, в дальнейшем ее обозначают М в отличие от M_F.

5. Указывают ординаты на эпюре М под центрами тяжести фигур эпюры M_F.

6. Определяют искомое перемещение с помощью правила Вере­щагина по формуле

Знак произведения ф_i у _i считается положительным, если обе эпюры расположены по одну сторону от оси элемента, и отрица­тельным, если по разные стороны. Если на рассматриваемом участке одна из эпюр отсутствует, то ф_i у _i = 0.

Пример 18. Определить горизонтальное перемещение точки А для схемы, изображенной на рис. 25, а. Для определения же­сткости EJ материал — сталь марки СтЗ, сечение — двутавровая балка № 18. Модуль продольной упругости Е= 2,1-Ю⁵ МПа.

Решение. 1. Определим изгибающие моменты в характерных точках от силы F= 15 кН.

81

82

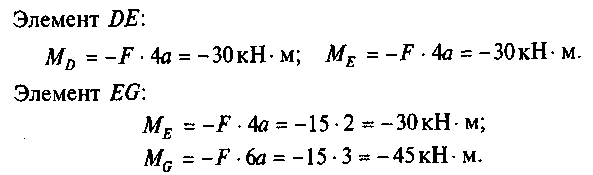
По найденным значениям строим эпюру M_F (рис. 25, б).

2. Разбиваем эпюру М_f на простейшие фигуры (рис. 25, в). Эпюра М_f разбита на семь фигур: три треугольника и четыре прямоугольника. Найдем их площади:

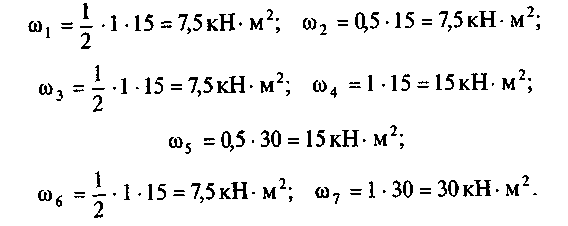
Укажем центры тяжести каждой из фигур: С₁ С₂, С₃, С₄, С₅,

C₆, С₇

3. По условию задачи требуется найти горизонтальное переме­щение точки А. Прикладываем единичную силу F = 1 в точке А и на­правляем ее горизонтально (по направлению искомого перемеще­ния). Направление действия силы принимается произвольно. При­мем его, как показано на рис. 25, г.

4. Определим изгибающие моменты в характерных точках от. силы F = 1.

83

По найденным значениям строим эпюру М (рис. 25, д).

5. Пользуясь прил. V, укажем ординаты на эпюре М под цв рами тяжести эпюр M_F (площадей ф_i):

у₁ = 0, так как моменты на участке АВ от F - 1 равны нулю; у₂ = 0,25, так как С₂ расположен в середине участка ВС; у₃ = 0,5 м; у₄ = 0,5 м; у₅ = 0,25 м; У₆ ⁼ У₇ =О, так как эпюры М на этом участке нет.

6. Определим искомое перемещение:

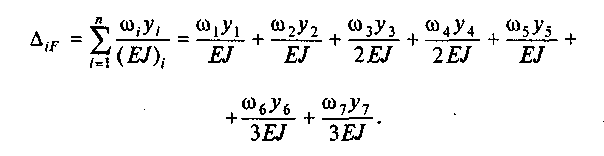
Подставим числовые значения и, учитывая, что ^ = О, у₆ = у₇ = 0) получим:

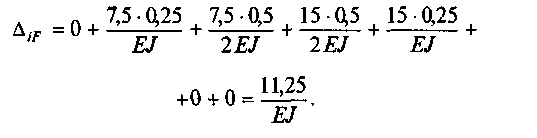
Для двутавровой балки № 18 момент инерции J_x = 1290 см⁴, сталь марки СтЗ, Е = 2,1-10⁵ МПа. Подставим эти значения в формулу для определения перемещения:

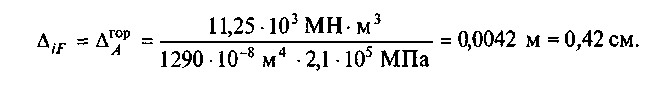
Пример 19. По условию примера 17 определить вертикальное перемещение точки В.

Решение. 1, 2. Эпюра M_f и площади, найденные в приме­ре 17, останутся теми же, так как схема рамы и нагрузка не из­менились. _

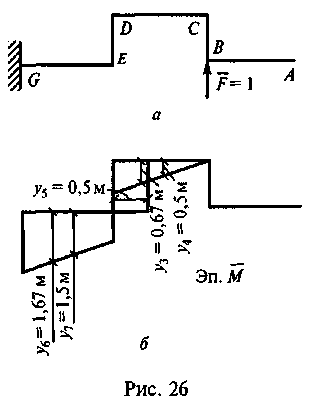
3. Прикладываем в точке В единичную силу F = 1 вертикально (по направлению искомого перемещения). Направление дейст­вия силы выбирается произвольно, например вверх (рис. 26, а). Очевидно, что перемещение направлено вниз. Проверим это.

84

4. Определим изгибающие мо­менты в характерных точках от F = l.

5. Пользуясь прил. V, определим ординаты на единичной эпюре под центрами тяжестей площадей ф_i (рис. 26, б):

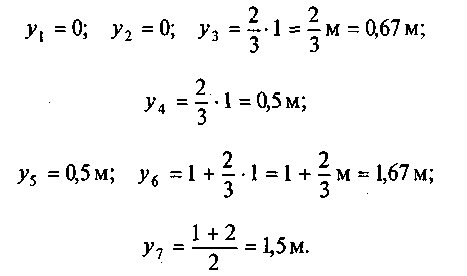
6. Определим искомое перемещение:

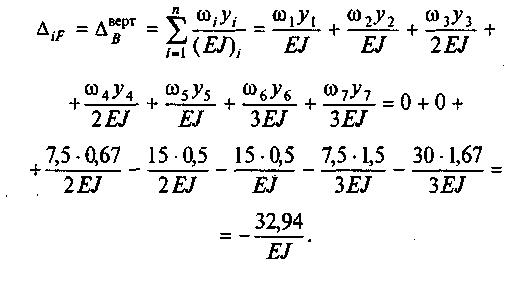
85

Подставим J_x = 1290 см⁴ и Е = 2,1 • 10⁵ МПа в формулу для определения перемещения:

Ответ'.

Знак «минус» свидетельствует о том,

что точка В перемещается в сторону, противоположную дейст­вию силы F = 1, т. е. вниз.

Задание для самостоятельной работы 10. Определить перемещение точ­ки D по данным одного из вариантов, показанных на рис. 27. Для нечет­ных вариантов определить вертикальное перемещение точки D, для чет­ных вариантов — горизонтальное. При определении жесткости EJ матери_: ал — сталь марки СтЗ, сечение — двутавровая балка № 20.

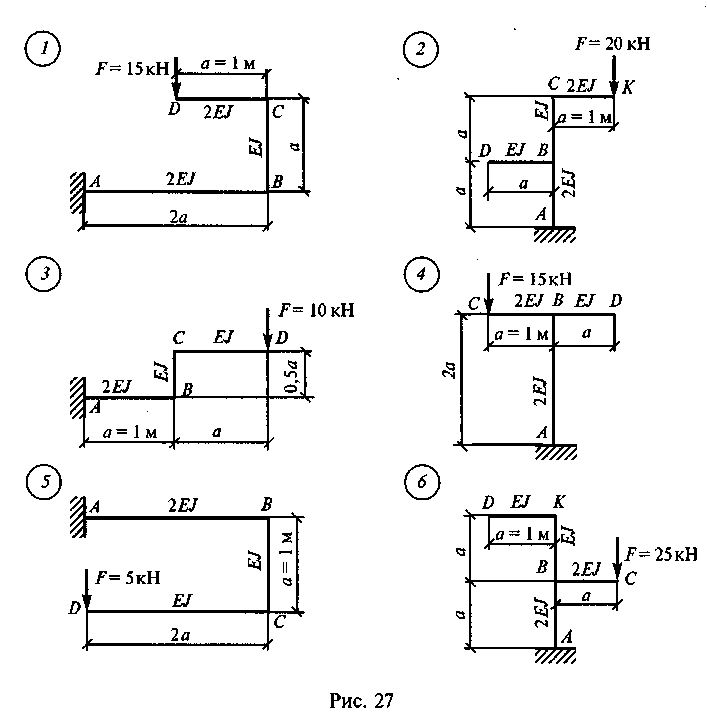
86

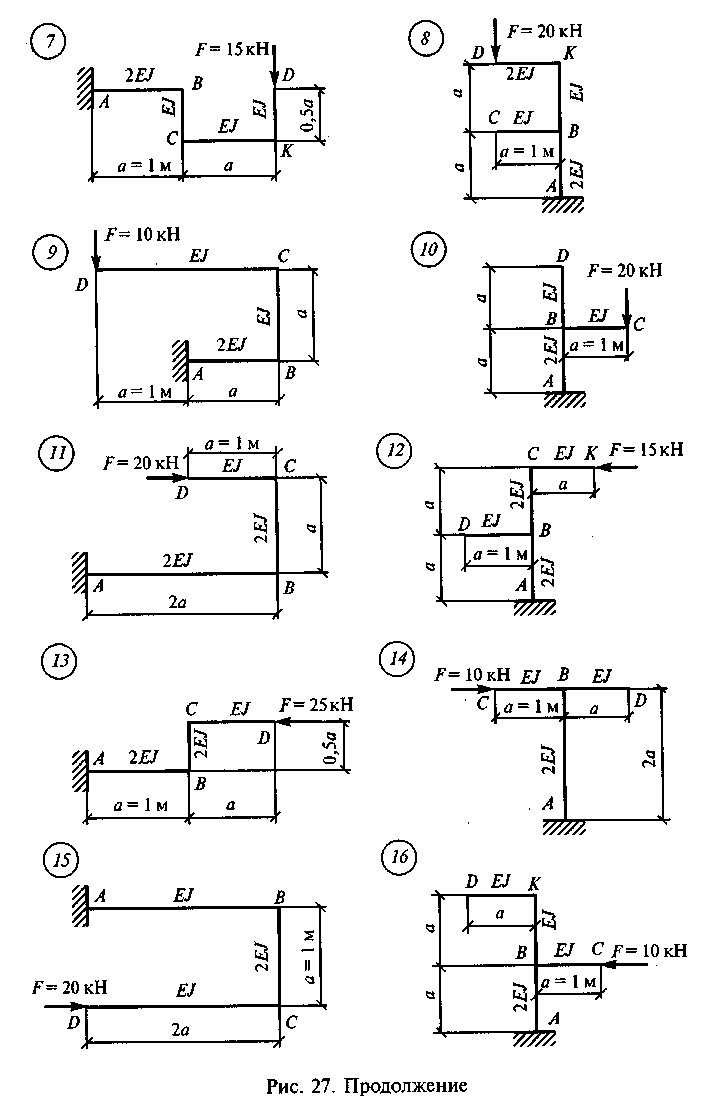
87

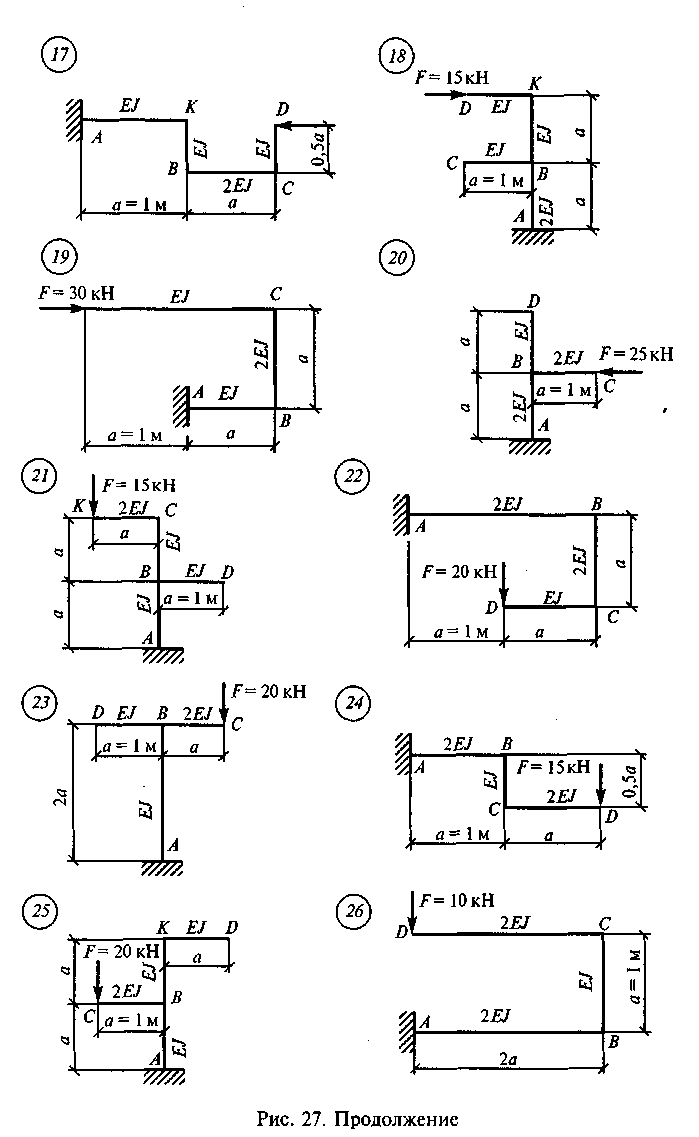
88

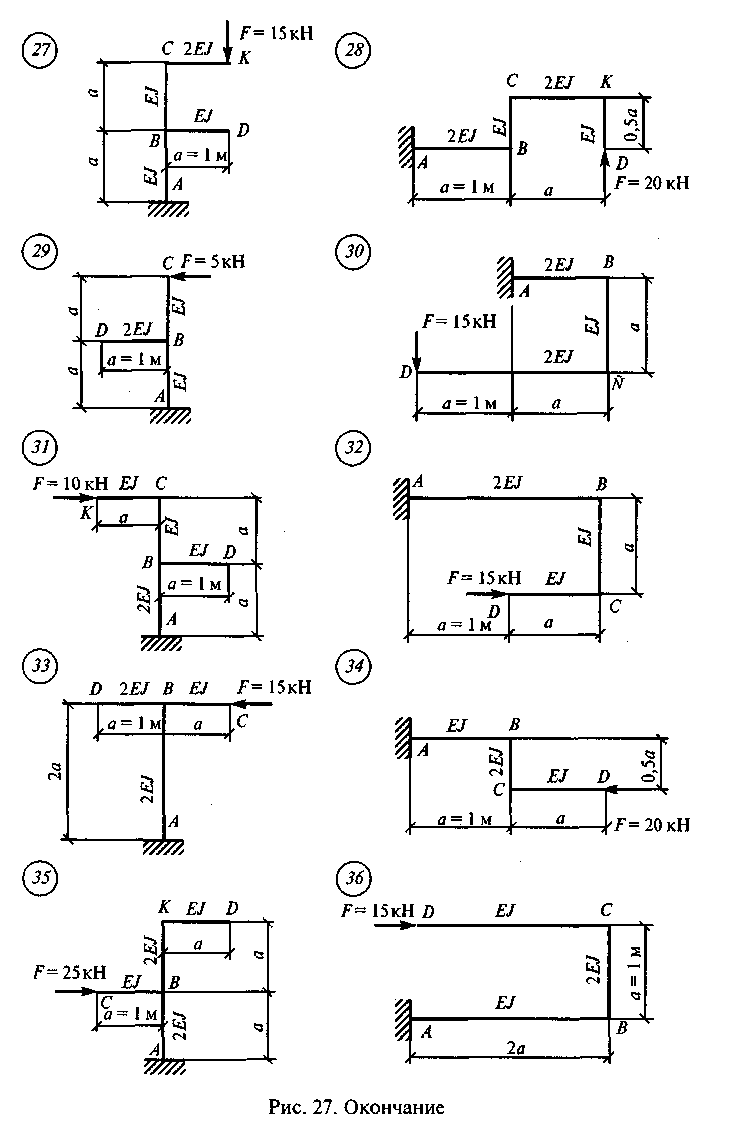
89