3.2. Обобщение метода бпф

Метод для ряда из 4 членов можно обобщить на любое другое количество членов ряда с основанием 2 (N = 2, 4, 8, 16, 32, ...) [16]. Составим ДПФ для выборки из 8 значений сигнала:

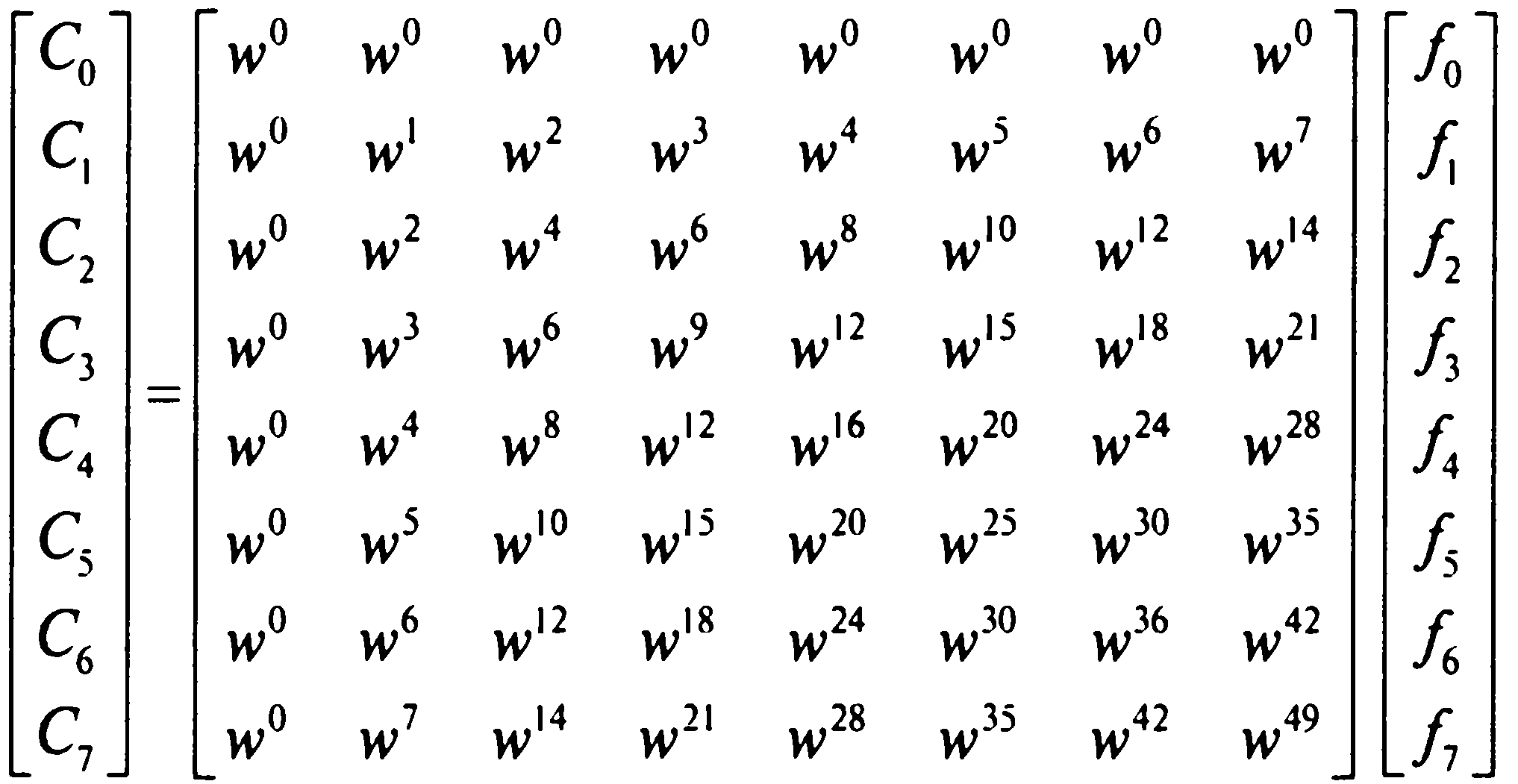
(11)

По диаграмме значений поворотных коэффициентов определяем их периодичность. Делаем соответствующие замены, группируем по чётным и нечётным индексам значений сигнала и выносим условный вектор-столбец, получаем:

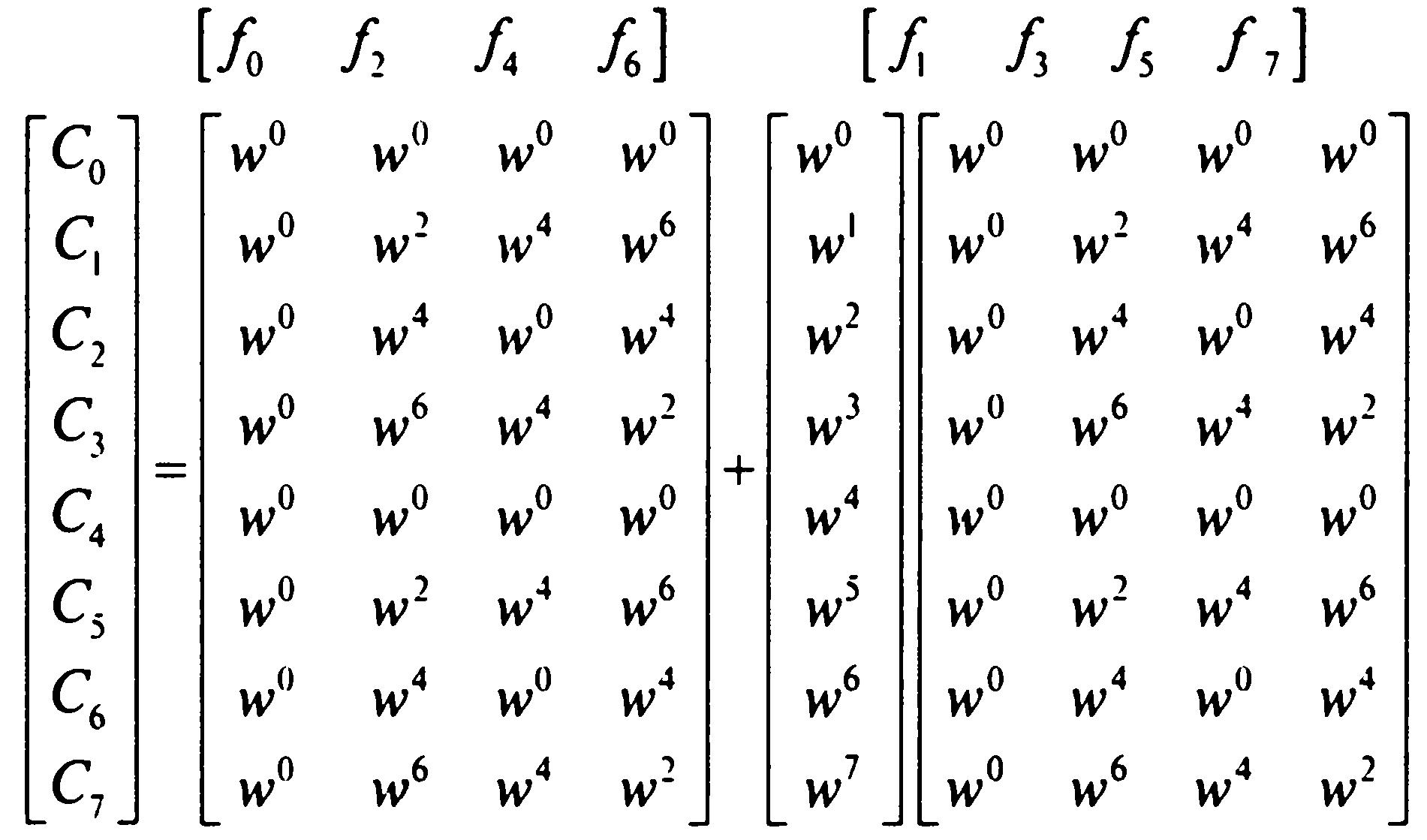
(12)

Подставляя в (12) значения для поворотных коэффициентов:

( 13)

( 14)

Получаем выражение:

(15)

Можно заметить, что матрицы, стоящие под группой с чётными и нечётными индексами значений сигнала одинаковы. Кроме того эти матрицы одинаковы с расстановкой значений w выражения (4*). Это означает, что если осуществить БПФ в каждой из групп сигналов с чётными и нечётными индексами, то, используя его результаты, можно выразить БПФ для ряда из 8 членов (Рис.4).

Оценим количество операций умножения. Если число данных N = 2^P, то число операций умножения для ДПФ равно N², в случае БПФ – N·P/2. Если число данных не велико, то и разница в числе операций незначительна. Но, к примеру, при N = 2¹⁰, для ДПФ получим ≈1050000, а для БПФ достаточно ≈5000 операций умножения.

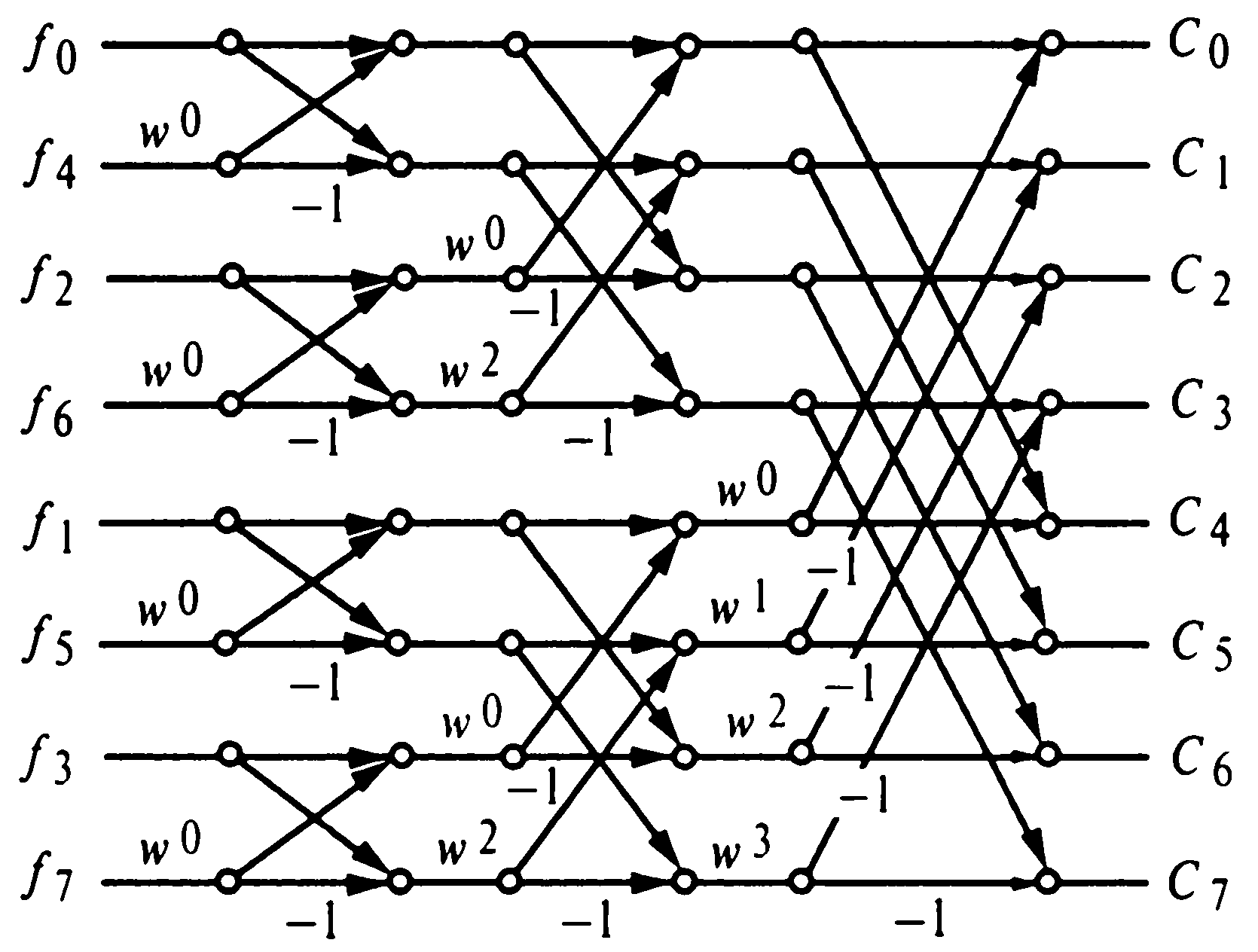
Рисунок 4. Схема алгоритма БПФ для ряда из 8 членов

Итак, прогнозируя развитие процесса можно сделать следующий вывод. Если повторять метод вычисления «бабочкой» и соответствующую перестановку ряда значений сигнала, переходя из БПФ для ряда из 4 членов к БПФ для ряда из 8 членов, то, в конце концов, можно осуществить быстрое преобразование Фурье сигнала для ряда, состоящего из любого числа членов количеством, равном 2^L.

3.3. Метод сортировки

Как следствие предыдущих двух пунктов, одной из главных ступеней алгоритма БПФ является метод вычисления «бабочкой». Ещё один важный момент заключается в последовательных разбиениях ряда значений сигнала на две группы и перестановке значений сигнала таким образом, чтобы в последующем прийти к методу вычислений «бабочкой».

Данная процедура называется двоично-инверсной перестановкой. Эта техника сортировки позволяет выполнить перенумерацию отсчетов, переписав номер отсчета в двоичной системе в обратном направлении (Рис.5).

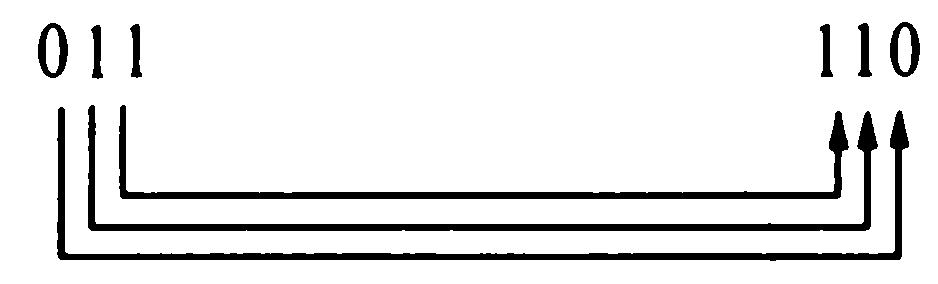
Рисунок 5. Двоично-инверсная запись индекса значения сигнала

Например, f₄ имеет индекс в десятичной системе счисления 4₁₀ = 100₂, если же 100₂ переписать справа налево, то получим 001₂, то есть f₄ после разбиения на группы с четными и нечетными индексами перед первой операцией «Бабочка» встанет на место f₁, которая в свою очередь встанет на место f₄. По аналогичному правилу поменяются местами все отсчеты, при этом некоторые останутся на месте, в частности f₂, так как если 2₁₀ = 010₂ переписать справа налево, то все равно останется 010₂, аналогично f₀, f₅ и f₇. Очень важно понять, что данный метод перенумерации должен применяться при записи числа в двоичной системе, состоящей из L разрядов. В приведенном примере использовалось 3 разряда двоичного числа, но если же L = 4 (N = 2⁴ = 16), то необходимо записать число при использовании 4 разрядов. В этом случае 2₁₀ = 0010₂ и после переписывания получим 0100₂, то есть при N = 16 f₂ не останется на месте, а поменяется местами с f₄.