3. Энергия волны, групповая скорость

Любая волна переносит энергию, но при этом не происходит переноса вещества. Так как волны занимают значительный объем пространства, и энергия может быть распределена в пространстве неравномерно, вводят энергетические характеристика волны.

Объемной плотностью энергии w называется энергия единицы объема:

,

[w]си = 1 Д ж/м3.

(12)

Потоком энергии Ф называется скалярная величина, равная энергии, переносимой волной через некоторую поверхность в единицу времени:

или ,

[Ф]си = 1 Дж/с = 1 Вт.

(13)

Для характеристики переноса энергии в разных точках пространства используется величина, называемая плотностью потока энергии.

Плотностью потока энергии называется векторная физическая величина, численно равная потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению переноса энергии. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.

или

[j]си = 1 Вт/м2 .

(14)

Из соотношения (14) следует, что полный поток энергии через некоторую поверхность S, охваченную волной, равен сумме элементарных потоков:

.

(15)

Через площадку S_ будет перенесена за время t энергия W, заключенная в объеме цилиндра с основанием S_ и высотой vt, где v - фазовая скорость волны. Эта энергия равна: . Подставляя это выражение в плотность потока энергии, получаем:

или в векторном виде

(16)

Таким образом, вектор плотности потока энергии равен произведению объемной плотности энергии на вектор фазовой скорости волны и направлен всегда в сторону переноса энергии волной. Значение объемной плотности энергии w, а, следовательно, и вектор плотности потока энергии j для упругих и электромагнитных волн различны. Для упругих волн вектор плотности потока энергии называется вектором Умова, а для электромагнитных волн - вектором Пойнтинга. Вектор плотности потока энергии различен в разных точках пространства, а в данной точке для гармонической волны изменяется со временем по закону квадрата синуса, поэтому чаще используют его среднее значение, называемое интенсивностью волны.

Интенсивностью волны I называется модуль среднего по времени значения плотности потока энергии, переносимой волной.

I = | < j > |  А2

[I]си = 1 Вт/м2 .

(17)

Интенсивность волны - величина скалярная, численно равная энергии, переносимой волной за единицу времени сквозь единицу площади поверхности, нормальной к направлению распространения волны.

Интенсивность гармонической волны всегда пропорциональна квадрату ее амплитуды.

Скорость переноса энергии волной равна скорости перемещения в пространстве поверхности, соответствующей максимальному значению объемной плотности w энергии волны. Для бесконечных гармонических волн эта скорость равна фазовой скорости волны при распространении в любой среде. Любая реальная волна не является бесконечной гармонической волной. Если в среде распространяется волновой импульс или цуг волн, то, основываясь на принципе суперпозиции, его можно представить как сумму гармонических волн или волновой пакет. Каждая гармоническая составляющая, входящая в волновой пакет, имеет свою амплитуду и частоту.

Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства (рис.6).

Волновой импульс шириной х может быть представлен как суперпозиция гармонических волн, частоты которых заключены в интервале .

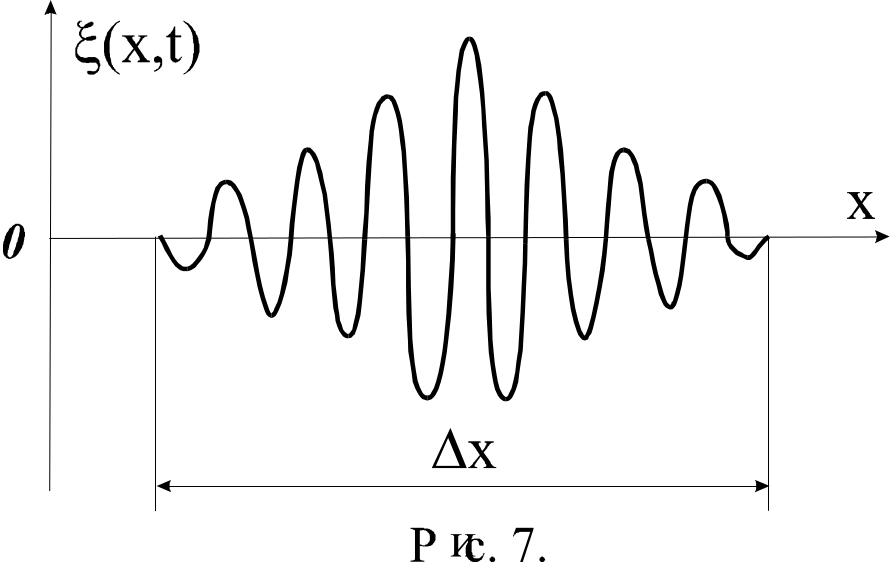
Рис. 6

В отсутствии дисперсии все волны, образующие пакет, распространяются с одинаковой фазовой скоростью, поэтому его форма не меняется в процессе распространения. В диспергирующей среде фазовая скорость отдельных составляющих пакета различна, так как зависит от частоты:

.

(18)

В диспергирующей среде волновой пакет со временем «расплывается», так как его ширина увеличивается. Если дисперсия невелика, то расплывание пакета происходит не слишком быстро. В этом случае пакету можно приписать так называемую групповую скорость u.

Групповой скоростью называется скорость переноса энергии волной или скорость перемещения центра волнового пакета.

В диспергирующих средах групповая скорость отличается от фазовой.

Связь групповой скорости волны с фазовой имеет вид:

.

(19)

В отсутствии дисперсии и u = v, то есть групповая скорость совпадает с фазовой. Понятие групповой скорости применимо только при условии, что поглощение энергии волны в данной среде невелико. При значительном затухании волны понятие групповой скорости утрачивает смысл. Понятие групповой скорости используется при измерении дальности в радиолокации, в системах управления космическими объектами, именно она является реальной скоростью передачи информации: u  C, V может быть и больше. C  3  10⁸ м/с - скорость света в вакууме.