2. Звуковые волны и их характеристики

Звуковыми или акустическими волнами называются упругие волны, имеющие частоту в пределах от 1 6 Гц до 20 кГц и воспринимаемые человеческих ухом.

Упругие волны с частотами, меньшими 16 Гц, называются инфразвуком; с частотами, большими 20 кГц, - ультразвуком.

Раздел физики, изучающий свойства звуковых волн, закономерности их возбуждения и распространения называется акустикой.

Ультразвук и инфразвук человеческое ухо не слышит. Основными характеристиками звуко­вых волн являются: интенсивность волны, уровень громкости, акустический спектр, высота и тембр звука.

Найдем интенсивность плоской гармонической волны. Поэтому практически используют модуль среднего значения плотности потока энергии, который называется интенсивностью волны. Для упругих волн, учитывая, что = 0,5, получаем:

(5)

Таким образом, интенсивность упругой волны прямо пропорциональна волновому сопро­тивлению среды , квадрату амплитуды волны I = А² и квадрату частоты волны. Эти за­висимости определяют важнейшие характеристики звуковых волн.

Для того чтобы вызвать в человеческом ухе звуковое ощущение, звуковая волна должна обладать некоторой минимальной интенсивностью.

Порогом слышимости называется минимальная интенсивность звуковой волны I _min которая вызывает звуковое ощущение в человеческом ухе.

Порогом болевого ощущения называется максимальное значение интенсивности I_mах, при котором звуковая волна перестает восприниматься, как звук и вызывает только ощуще­ние боли и давления.

Значения I_maх и I _min зависят от частоты звука и в среднем составляют I _min 10 ^-12 Вт/м² и I_mах 10 Вт/м².

Интенсивность звука является величиной, объективно характеризующей упругую волну независимо от вызываемого ею звукового ощущения. Субъективной характеристикой звука, связанной с его интенсивностью и вызываемым в ухе звуковым ощущением, является уровень громкости.

Уровнем громкости звука называется логарифм отношения интенсивности I данного звука к порогу слышимости I _min.

L = (6)

Единица измерения уровня громкости L называется белом (Б). Как правило, используется единица, в 10 раз меньшая - 1 децибел (1 дБ). При расчете в децибелах уровня громкости звуковой волны с интенсивностью I = А² и амплитудой А

L = 10 (7)

Диапазон интенсивностей от I _min до I_mах, при которых звуковая волна вызывает звуковое ощущение в ухе, соответствует значениям уровня громкости от 0 до 130 дБ. Например, ти­канье часов соответствует уровню громкости 20 дБ, громкая речь - 70 дБ, шум реактивного двигателя на расстоянии 3 м - 130 дБ.

Любая реальная звуковая волна является наложением гармонических волн с опреде­ленным набором частот. Ее можно разложить в ряд Фурье на простые гармоники (моды), то есть получить так называемый акустический спектр.

Зависимость I() интенсивности отдельных гармонических составляющих звуковой волны от частоты этих составляющих называется акустическим спектром.

Если в звуке присутствуют колебания всех частот, заключенных в некотором интер­вале (_1, ₂), то акустический спектр называется сплошным (рис. 1). Сплошным акустическим спек­тром обладают шумы и шумоподобные звуки. Если звуковая волна состоит из колебаний дискретных частот _1, ₂ , _3……. _{n ,}то акустический спектр называется линейчатым (рис.2). Линей­чатым спектром обладают обычно музыкальные или тональные звуки.

Рис. 1

Рис. 2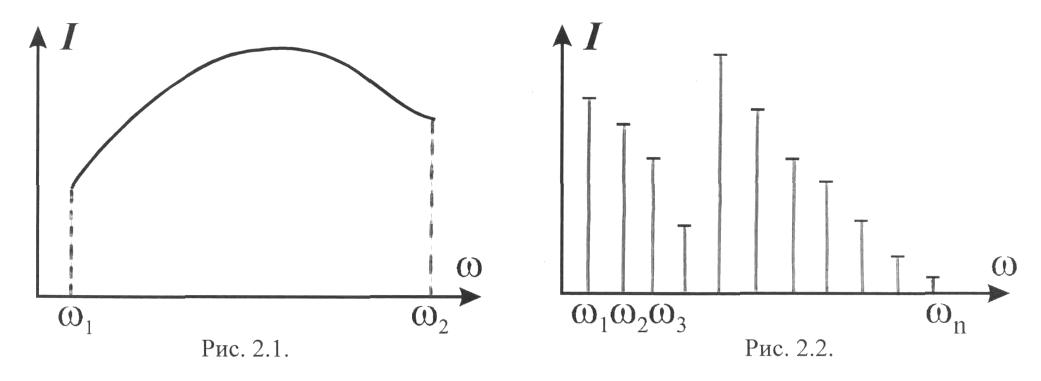

Спектральный состав звука, определяемый его акустическим спектром, называется тембром звука.

Высота тонального звука определяется частотой его основного тона: чем больше частота, тем выше тон. Основным тоном сложного музыкального звука называется тон, со­ответствующий наименьшей частоте ₁ в его спектре. Тоны, соответствующие остальным час­тотам спектра ₁, называются обертонами. Именно относительная интенсивность обертонов определяет тембр и окраску звука и позволяет отличить на слух звуки одинаковой высоты, излучаемые различными источниками.

Если приемник и источник звуковых волн движутся относительно среды с некоторыми скоростями и , при приеме волн возникает эффект Доплера.

Эффект Доплера называется зависимость частоты волн, воспринимаемых приемником, от скоростей движения источника волн и приемника по отношению к среде, в которой распространяется волна.

Пусть источник, движущийся относительно среды со скоростью излучает волну с частотой . В случае, если приемник и источник движутся вдоль соединяющей их прямой, формула Доплера (8) имеет вид:

. (8)

В формуле (8) необходимо учитывать изменение знаков скоростей и при изменении направления движения приемника или источника:  0 и  0,если происходит сближение источника;  0 и  0, если приемник удаляется от источника.

Из формулы Доплера следует, что при взаимном сближении приемника и источника воспринимаемая приемником частота волны оказывается больше частоты волны , излучаемая источником (  ). Если = =0 или = , то = , то есть частота не изменяется.