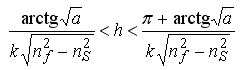- •2.1. Оптичні явища на границі розділу двох діелектричних середовищ
- •2.2. Закони Снелла
- •2.3. Повне внутрішнє відбивання
- •2.4. Закони Френеля
- •2.5. Кут Брюстера
- •2.7. Ефект Гуса-Хенхена
- •3.1. Модель зигзагоподібного поширення хвиль у тонкій плівці
- •3.2. Ефективна товщина хвилеводу
- •3.3. Моди плоского хвилеводу
- •3.4. Рівняння хвилеводних мод
- •3.5. Число мод плоского хвилеводу
- •3.6. Універсальні дисперсійні криві для плоского хвилеводу
- •4.1. Класифікація та основні типи планарних оптичних хвилеводів
- •4.2. Елементи вводу/виводу випромінювання у хвилевід
- •4.2.1. Поперечні елементи зв’язку
- •4.2.2. Поздовжні елементи зв’язку
- •4.3. Елементи зв’язку між оптичними хвилеводами
- •4.3.1. Зв’язок між плоскими планарними хвилеводами
- •4.3.2. Зв'язок між плоскими та канальними хвилеводами
- •4.3.3. Зв'язок між канальними хвилеводами
- •4.3.4. Зв'язок між планарними і волоконними хвилеводами
- •4.4. Перетворювачі мод
- •5.1. Матеріали для планарних хвилеводів
- •5.2. Процедура підготовки підкладки
- •5.3. Методи виготовлення тонкоплівкових хвилеводів
- •5.3.1. Метод розпилення
- •5.3.2. Метод плазмової полімеризації
- •5.3.3. Метод осадження з розчину
- •5.3.4. Метод дифузії
- •5.3.5. Метод іонного обміну
- •5.3.6. Метод іонної імплантації
- •5.4. Методи виготовлення канальних хвилеводів
- •6.1. Оптичні втрати та коефіцієнт затухання
- •6.2. Розсіяння
- •6.3. Абсорбція
- •6.4. Випромінювання
3.4. Рівняння хвилеводних мод
При формуванні моди в поперечному напрямку оптичного хвилеводу виникає стояча хвиля. Для виникнення стоячої хвилі повинна виконуватись умова: зсув фази світлової хвилі, яка рухається від верхньої границі хвилеводного шару до нижньої і назад, враховуючи відбивання на нижній границі “плівка-підкладка” та верхній границі “плівка-покриття”, має бути кратним 2π. З цього випливає, що для формування моди кут поширення світлових променів не може бути довільним, і тільки ті світлові промені, які задовольняють дану умову, можуть поширюватися.
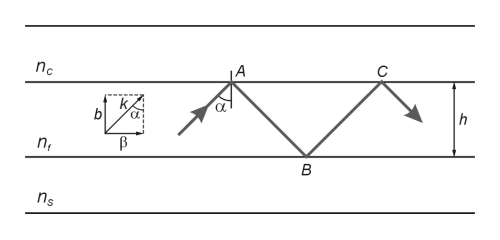
При русі хвилі з точки А до точки В проходить зсув фази рівний:
ΔφAB = bh = kh cos α
В результаті повного внутрішнього відбивання від нижньої границі розділу в точці В хвиля отримує зсув фази:
ΔφB = –ΔφS
Зсув фази хвилі при русі з точки В до точки С становить:
ΔφBC = bh = kh cos α
І, нарешті, зсув фази в точці С в результаті ПВВ рівний:
ΔφC = –ΔφC
Таким чином, можна записати:
2kh cos α – ΔφS – ΔφC = 2πm
де k – хвильове число, h – товщина хвилеводу, m – ціле число (0, 1, 2, …), яке визначає порядок моди.
Даний вираз називається умовою поперечного резонансу або рівнянням хвилеводних мод, оскільки він визначає моди оптичного хвилеводу. Якщо відомі параметри хвилеводу, то можна визначити кут поширення хвиль для моди m-го порядку.
3.5. Число мод плоского хвилеводу
У плоскому планарному хвилеводі можуть поширюватись тільки ТЕ- і ТМ-моди, оскільки лише для них спостерігаються резонансні умови. Кут поширення світлових хвиль у хвилеводі може приймати дискретні значення в межах від αS до π/2. Мода найнижчого 0-го порядку (m = 0), яка називається основною модою хвилеводу, поширюється у хвилеводі під максимальним кутом α, який наближається до π/2, а мода найвищого порядку поширюється у хвилеводі під мінімальним кутом α, який є найближчим до граничного кута αS. Таким чином, знаючи найвищий порядок моди хвилеводу, можна визначити число мод хвилеводу. Для визначення числа мод хвилеводу користуються рівнянням хвилеводних мод.
Максимальний порядок ТЕ-моди визначається з допомогою наступного виразу:
![]()
Враховуючи цей вираз, число ТЕ-мод у хвилеводі буде визначатись наступним чином:
![]()
Результати розрахунку m і N з допомогою даних виразів необхідно завжди округлювати до цілих, оскільки m і N не можуть приймати дробових значень.
Якщо nC = nS , то a = 0 і arctg √a = 0. При nC ≠ nS і nS ≈ nf , коефіцієнт а → ∞ і arctg √a → π/2. Тому, для визначення числа мод може використовуватись наближена формула:
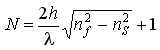
Для ТМ-мод вирази для розрахунку максимального порядку моди і числа мод мають такий же самий вигляд як і для ТЕ-мод за винятком коефіцієнта асиметрії хвилеводної структури, який для ТМ-мод визначається з виразу:
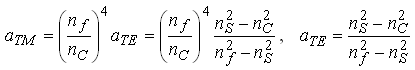
Оскільки в планарному хвилеводі можуть збуджуватись тільки ТЕ- і ТМ-моди, то загальну кількість мод у хвилеводі можна оцінити з допомогою виразу:
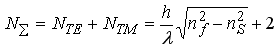
Умовою розповсюдження у плоскому хвилеводі тільки однієї моди є:
1 < N < 2 або 0 < m < 1
У такому випадку, якщо відомі показники заломлення підкладки, хвилеводного шару і покриття, товщина хвилеводного шару повинна задовольняти наступну умову: