
- •1). Первообразная и неопределённый интеграл. Таблица основных неопределённых интегралов.
- •2).Замена переменной и интегрирование по частям под знаком неопределённого интеграла.
- •6). Интегралы вида: , .
- •7). Интегралы вида: .
- •10). Понятие определённого интеграла, основные свойства определённого интеграла, его вычисление.
- •11.Вычисление площадей плоских фигур, объёмов тел и длин дуг с помощью определённого интеграла.
- •11’.Интегрирование по частям и замена переменной под знаком определённого интеграла.
- •12. Несобственные интегралы 1-го рода.
- •13. Несобственные интегралы 2-го рода.
- •14. Понятие функции нескольких переменных. Предел в точке, непрерывность.
- •15. Частные производные функции двух аргументов, их геометрический смысл.
- •16. Полный дифференциал функции двух и трёх переменных.
- •17. Производные сложной функции нескольких аргументов.
- •19. Дифференцирование неявных функций.
- •20. Частные производные высших порядков.
- •21. Локальный экстремум функции двух аргументов.
- •22. Условный экстремум. Метод множителей Лагранжа.
- •23. Наименьшее и наибольшее значения функции двух аргументов в замкнутой области.
- •24. Двойной интеграл в декартовых координатах. Определение, основные свойства.
- •25. Вычисление двойного интеграла в дск.
- •26. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •27. Вычисление площадей и объёмов с помощью двойного интеграла.
- •28. Тройной интеграл. Определение, основные свойства. Его вычисление в декартовых координатах.
- •29. Цилиндрические координаты. Тройной интеграл в цилиндрических координатах.
- •30. Сферические координаты. Тройной интеграл в сферических координатах.
- •31. Криволинейный интеграл 1-го рода, его свойства и вычисление.
- •32. Криволинейный интеграл 2-го рода, его определение, свойства и вычисление.
- •33. Криволинейный интеграл 2-го рода как работа переменной силы на криволинейном пути.
- •34. Вычисление площади плоской фигуры с помощью кри-2.
- •35. Формула Грина.
- •36. Независимость криволинейного интеграла от пути интегрирования. Нахождение функции по её полному дифференциалу.
- •37. Поверхностный интеграл 1-го рода, его свойства и вычисление. Поверхностный интеграл 2-го рода.
- •38. Вычисление массы поверхности.
- •39. Скалярное поле, производная по направлению.
- •40. Градиент.
- •41. Векторное поле. Дивергенция.
- •42. Поток векторного поля.
- •43. Формула Остроградского.
- •44. Формула Стокса.
- •45. Оператор Гамильтона.
- •46. Оператор Лапласа.
- •47. Потенциальное векторное поле и его свойства.
- •48. Соленоидальное векторное поле.
- •49. Гармоническое векторное поле.
29. Цилиндрические координаты. Тройной интеграл в цилиндрических координатах.
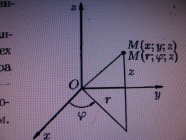 Для
вычисления 3-го инт-ла часто исп-ют так
называемые цилиндрич. корд. Положение
т. M(x,y,z)
в пространсве Oxyz
можно определить заданием 3-х чисел r,
Для
вычисления 3-го инт-ла часто исп-ют так
называемые цилиндрич. корд. Положение
т. M(x,y,z)
в пространсве Oxyz
можно определить заданием 3-х чисел r,
 ,
где r
– длина радиуса-вектора проекции т.М
на плоскость Oxy,
,
где r
– длина радиуса-вектора проекции т.М
на плоскость Oxy,
 - угол, образованный этим радиусом-вектором
с с осью Ox,
z
– аппликата т.М. Эти 3 числа (
- угол, образованный этим радиусом-вектором
с с осью Ox,
z
– аппликата т.М. Эти 3 числа ( )
наз-ся цилиндрическими
координатами т.М.
)
наз-ся цилиндрическими
координатами т.М.
Цилиндрич.
координаты точки связаны с ее декартовыми
координатами следующими соотношениями:
 ,
,
 .
Возьмем цилиндрич. координаты r,
и вычислим Якобиан преобразования:
.
Возьмем цилиндрич. координаты r,
и вычислим Якобиан преобразования:
 .
Ф-ла замены переменных принимает вид:
.
Ф-ла замены переменных принимает вид:
 .
Т.о., вычисление 3-го инт-ла приводится
к интегрированию по r,
по
,
по z
аналогично тому, как это делается в
декартовых координатах.
.
Т.о., вычисление 3-го инт-ла приводится
к интегрированию по r,
по
,
по z
аналогично тому, как это делается в
декартовых координатах.
Замечание:к цилиндрич. корд. следует переходить, если обл. интегр-ния образована цилиндрич. пов-тью.
30. Сферические координаты. Тройной интеграл в сферических координатах.
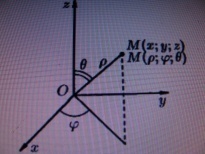 Сферич.
координатами
M(x,y,z)
пространства Oxyz
наз-ся тройка чисел
Сферич.
координатами
M(x,y,z)
пространства Oxyz
наз-ся тройка чисел
 ,
где
,
где
 - длина радиуса-вектора точки M,
- угол, образованный проекцией
радиус-вектор OM
на плоскость Oxy
и осью Ox,
- длина радиуса-вектора точки M,
- угол, образованный проекцией
радиус-вектор OM
на плоскость Oxy
и осью Ox,
 - угол отклонения радиуса-вектора OM
от оси Oz.
Сферич. координаты
связаны с декартовыми координатами x,
y,
z:
- угол отклонения радиуса-вектора OM
от оси Oz.
Сферич. координаты
связаны с декартовыми координатами x,
y,
z:
 (
( ).
В нек. случаях вычисление 3-го инт-ла
удобно производить, перейдя к сферич.
координатам. Для этого нужно воспользоваться
ф-лой замены переменных в 3-ом инт-ле.
Т.к. Якобиан:
).
В нек. случаях вычисление 3-го инт-ла
удобно производить, перейдя к сферич.
координатам. Для этого нужно воспользоваться
ф-лой замены переменных в 3-ом инт-ле.
Т.к. Якобиан:
 .
То:
.
То:

 .
.
Замечание:
перходить
к сферич. коорд., когда обл. интегрирования
V
есть шар (ур-ние его границы
 в сферич. коорд. имеет вид
в сферич. коорд. имеет вид
 )
или его часть, а также если подынтегральная
ф-ция имеет вид
)
или его часть, а также если подынтегральная
ф-ция имеет вид
 .
.
31. Криволинейный интеграл 1-го рода, его свойства и вычисление.
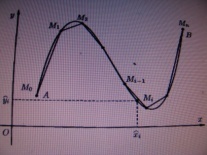 Пусть
на плоскости Oxy
задана непрерывная кривая АВ (или L)
длины
Пусть
на плоскости Oxy
задана непрерывная кривая АВ (или L)
длины
 .
Рассмотрим непрерывную ф-цию
.
Рассмотрим непрерывную ф-цию
 ,
определенную в точках дуги АВ. Разобьем
кривую АВ точками
,
определенную в точках дуги АВ. Разобьем
кривую АВ точками
 на n
произвольных дуг
на n
произвольных дуг
 с длинами
с длинами
 .
Выберем на каждой дуге
произв. т-ку (
.
Выберем на каждой дуге
произв. т-ку ( )
и составим сумму:
)
и составим сумму:
 .
Ее наз-ют интегральной
суммой для
ф-ции f(x,y)
по
кривой AB.
Пусть
.
Ее наз-ют интегральной
суммой для
ф-ции f(x,y)
по
кривой AB.
Пусть
 – наиб. из длин дуг деления. Если при
– наиб. из длин дуг деления. Если при
 (тогда n
(тогда n )
сущ-ет конечный предел интегр-ых сумм,
то его наз-ют криволинейным
интегралом 1-го рода (КРИ-1):
)
сущ-ет конечный предел интегр-ых сумм,
то его наз-ют криволинейным
интегралом 1-го рода (КРИ-1): .
.
Теорема:
если ф-ция f(x,y)
непрерывна в каждой точке гладкой
кривой (в каждой точке (x,y) сущ-ет касательная к данной кривой и
положение ее непрерывно меняется при
перемещении точки по кривой), то КРИ-1
сущ-ет и его вел-на не зависит ни от
способа разбиения кривой на части, ни
от выбора точек в них.
сущ-ет касательная к данной кривой и
положение ее непрерывно меняется при
перемещении точки по кривой), то КРИ-1
сущ-ет и его вел-на не зависит ни от
способа разбиения кривой на части, ни
от выбора точек в них.
Св-ва
КРИ-1:1. ,
т.е. КРИ-1 не зависит от напр. пути
интегрирования.
,
т.е. КРИ-1 не зависит от напр. пути
интегрирования.
2. ,
c=const.
,
c=const.
3. .
.
4. ,
если путь инт-ния L
разбит на части
,
если путь инт-ния L
разбит на части
 и
и
 такие, что
такие, что
 и
и
имеют единственную общую точку.
и
и
имеют единственную общую точку.
5.если
для точек кривой L
выполнено неравенство
 ,
то
,
то
 .
.
6. ,
-длина
кривой АВ.
,
-длина
кривой АВ.
7.если
ф-ция f(x,y)
непрерывна на кривой АВ, то на этой
кривой найдется точка ( )
такая, что
)
такая, что
 (теорема о среднем).
(теорема о среднем).
Вычисление КРИ-1:1.параметрич. представление кривой инт-ния:
Если
кривая АВ задана парам. ур-ми
 ,
где
,
где
 -непрерывно
дифф-мые ф-ции параметра t,
причем тке.А соответствует
-непрерывно
дифф-мые ф-ции параметра t,
причем тке.А соответствует
 ,
точке В – t=
,
точке В – t= ,
то
,
то
 .
Аналогично для ф-ции
.
.
Аналогично для ф-ции
.
2.Явное
представление кривой инт-ния:
если кривая АВ задана
 ,
где
,
где
 - непрерывно дифф-мая ф-ция, то
- непрерывно дифф-мая ф-ция, то
 .
.
 .
.
3.Полярное
представление кривой инт-ния:
если плоская кривая L
задана ур.
 в ПСК, то
в ПСК, то
 и
и
 .
Во
всех 3-х случаях нижний предел всегда
меньше верхнего.
.
Во
всех 3-х случаях нижний предел всегда
меньше верхнего.
Масса
кривой:
масса мат. кривой АВ опр-ся ф-ой
 ,
где
,
где
 - плотность кривой в т.М. Разобьем АВ на
n
эл-х дуг
- плотность кривой в т.М. Разобьем АВ на
n
эл-х дуг
 .
Пусть
.
Пусть
 - произв. точка дуги
.
Считая приближенно участок пути
однородным, т.е. считая, что плотность
в кажд. точке дуги такая же, как и в точке
,
найдем приближенное значение массы
- произв. точка дуги
.
Считая приближенно участок пути
однородным, т.е. считая, что плотность
в кажд. точке дуги такая же, как и в точке
,
найдем приближенное значение массы
 дуги
:
дуги
:
 .
Суммируя, находим приближенное значение
массы m:
.
Суммируя, находим приближенное значение
массы m:
 За массу кривой АВ примем преде суммы
при условии, что
За массу кривой АВ примем преде суммы
при условии, что
 :
:
 ,
,
 .
(предел сущ-ет, если криая АВ гладкая,
а плотность задана непрерывной в каждой
точке АВ ф-цией).
.
(предел сущ-ет, если криая АВ гладкая,
а плотность задана непрерывной в каждой
точке АВ ф-цией).
 .
.
