27. Вычисление площадей и объёмов с помощью двойного интеграла.
Рассмотрим
тело, ограниченное сверху поверхностью
z=f(x,y)
,
снизу – замкнутой областью D
плоскости Oxy,
с боков – цилиндрич. поверхностью,
образующая кот. || оси Oz,
а направляющей служит граница обл. D.
Такое тело наз-ся цилиндрическим. Найдем
его объем. Для этого разобьем обл. D
(проекция пов-ти z=f(x,y)
на плоскость Oxy)
произвольным образом на n
областей
,
площади которых равны
.
Рассмотрим цилиндрич. столбики с
основаниями
,
ограниченные сверху кусками пов-ти
z=f(x,y).
В своей совокупности они составляют
тело V.
Обозначим объем столбика с основанием
через
,
получим
.
Возьмем на каждой площадке
произвольную точку
и заменим каждый столбик прямым цилиндром
приближенно равен объему
цилиндрич. столбика, т.е.
.
Тогда получаем:
.
Это равенство тем точнее, чем больше
число n
и чем меньше размеры «элементарных
областей»
неограниченно увеличивается (
),
а каждая площадка стягивается в точку
(
),
за объем V
цилиндрич. тела, т.е.
.
,
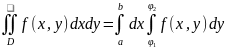представляет собой способ вычисления
2-го интеграла в ДСК. Правую часть ф-лы
наз-ют двукратным ит-ом от ф-ции f(x,y)
по обл. D.
При этом
нназ-ют внутренним инт-ом. Для вычисления
двукратного инт-ла сначала берем
внутренний инт-л, считая x
пост., затем берем внешний инт-л, т.е.
рез-т 1-го интег-ния интегрируем по х в
пределах от a
и b.
28. Тройной интеграл. Определение, основные свойства. Его вычисление в декартовых координатах.
Пусть
в замкнутой области V
пространства Oxyz
задана непрерывная ф-ция
.
Разбив область V
сеткой поверхностей на n
частей
и выбрав в каждой из них произвольную
точку
,
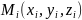составим интегральную сумму
для ф-ции
по обл. V
(
).
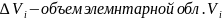Если предел инт-ной суммы сущ-ет при
неограниченном увеличении числа n
таким образом, что каждая «элементарная
область»
стягивается в точку (т.е. диаметр области
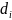стремится к 0), то его называют тройным
интегралом
от ф-ции
по обл. V
и обозначают:
.
Т.о. по определению:
.
Теорема: если ф-ция u=f(x,y,z) непрерывна в ограниченной замкнутой области V, то предел интегральной суммы существует и не зависит ни от способа разбиения области V на части, ни от выбора точек в них.
Свойства те же, что и у 2-го:
1.
.
2.
.
3.
.
4.
,
если в обл. V
ф-ция
.
Если в обл. интегрирования
,
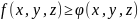то и
.
5.
.
6.Оценка
3-го интеграла:
,
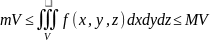m,
V-соотв.
наименьшее и наибольшее значения ф-ции
в области V.
7.Теорема
о среднем значении: если
непрерывна в замкнутой обл. V,
то в этой обл. сущ-ет такая т.
:
,
V
– объем тела.
В
ДСК вычисление 3-го инт-ла сводится к
послед-му вычислению ОИ. Пусть областью
интегр-ния V
явл-ся тело, ограниченное снизу пов-тью
,
сверху – поверхностью
,
причем
(
)
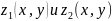– непрерывные ф-ции в замкнутой обл.
D,
являющейся проекцией тела на плоскость
Oxy.
Будем считать обл. V
– правильной в направлении оси Oz:
любая прямая, || оси Oz,
пересекает границу обл. не более чем в
2-х точках. Тогда для любой непрерывной
в обл. V
ф-ции f(x,y,z)
имеет место ф-ла:
,
сводящая вычисление3-го инт-ла к
вычислению 2-го инт-ла от однократного.
При этом сначала вычисляется внутренний
инт-л по переменной z
при пост. x,
y
в пределах изменения z.
Нижней границей инт-ла явл-ся аппликата
т.А – точки входа прямой, || оси Oz
в обл. V,
т.е.
;
верхней границей – аппликата т.В –
точки выхода прямой из обл. V,
т.е.
.
Результат вычисления этого интеграла
есть ф-ция 2-х переменных: x,
y.
Если обл. D
ограничена линиями x=a,
x=b
(a<b),
y=
и
,
где
и
- непрерывные на отрезке [a,b]
ф-ции, причем
,
то, переходя от 2-го инт-ла по обл. D
к повторному, получаем:
,
по кот. вычисляется 3-ной инт-л в ДСК.
Замечания: 1.если обл. V более сложная, чем рассмотренная, то ее следует разбить на конечное число таких областей (правильных), к кот. можно применить ф-лу. 2.порядок инт-ния в ф-ле, при опред. условиях, может быть иным.