
- •1). Первообразная и неопределённый интеграл. Таблица основных неопределённых интегралов.
- •2).Замена переменной и интегрирование по частям под знаком неопределённого интеграла.
- •6). Интегралы вида: , .
- •7). Интегралы вида: .
- •10). Понятие определённого интеграла, основные свойства определённого интеграла, его вычисление.
- •11.Вычисление площадей плоских фигур, объёмов тел и длин дуг с помощью определённого интеграла.
- •11’.Интегрирование по частям и замена переменной под знаком определённого интеграла.
- •12. Несобственные интегралы 1-го рода.
- •13. Несобственные интегралы 2-го рода.
- •14. Понятие функции нескольких переменных. Предел в точке, непрерывность.
- •15. Частные производные функции двух аргументов, их геометрический смысл.
- •16. Полный дифференциал функции двух и трёх переменных.
- •17. Производные сложной функции нескольких аргументов.
- •19. Дифференцирование неявных функций.
- •20. Частные производные высших порядков.
- •21. Локальный экстремум функции двух аргументов.
- •22. Условный экстремум. Метод множителей Лагранжа.
- •23. Наименьшее и наибольшее значения функции двух аргументов в замкнутой области.
- •24. Двойной интеграл в декартовых координатах. Определение, основные свойства.
- •25. Вычисление двойного интеграла в дск.
- •26. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •27. Вычисление площадей и объёмов с помощью двойного интеграла.
- •28. Тройной интеграл. Определение, основные свойства. Его вычисление в декартовых координатах.
- •29. Цилиндрические координаты. Тройной интеграл в цилиндрических координатах.
- •30. Сферические координаты. Тройной интеграл в сферических координатах.
- •31. Криволинейный интеграл 1-го рода, его свойства и вычисление.
- •32. Криволинейный интеграл 2-го рода, его определение, свойства и вычисление.
- •33. Криволинейный интеграл 2-го рода как работа переменной силы на криволинейном пути.
- •34. Вычисление площади плоской фигуры с помощью кри-2.
- •35. Формула Грина.
- •36. Независимость криволинейного интеграла от пути интегрирования. Нахождение функции по её полному дифференциалу.
- •37. Поверхностный интеграл 1-го рода, его свойства и вычисление. Поверхностный интеграл 2-го рода.
- •38. Вычисление массы поверхности.
- •39. Скалярное поле, производная по направлению.
- •40. Градиент.
- •41. Векторное поле. Дивергенция.
- •42. Поток векторного поля.
- •43. Формула Остроградского.
- •44. Формула Стокса.
- •45. Оператор Гамильтона.
- •46. Оператор Лапласа.
- •47. Потенциальное векторное поле и его свойства.
- •48. Соленоидальное векторное поле.
- •49. Гармоническое векторное поле.
23. Наименьшее и наибольшее значения функции двух аргументов в замкнутой области.
Есть ф-ция z=f(x,y), z-непрерывная в D и имеет непрер. частные производные. Чтобы найти ним. и наиб. значения ф-ции в области D, надо поступить так:
1). найти стацион. т-ки ф-ции и выбрать из них те, кот. попадают в область D (включая и границы).
2). не выясняя вопроса о том, есть ли в стаци. точках экстремум, найдем значения ф-ции в этих точках.
3). исследуем наиб. и наим. зн-ние данную ф-цию на границе области.
4). из всех найденных значений выбрать ним. и наиб. значения.
![]() Пример:
Пример:
 ,
в замкн. обл., огран. линиями:
,
в замкн. обл., огран. линиями:
 .
.
1).
 .
.
 .
.
 .
.
 .
.
2).
OA: y=0 ;
;
 .
.
3).
OB: x=0
 ,
OB[0,4];
,
OB[0,4];
 .
.
 подставим
в исх. z:
подставим
в исх. z:
 .
.
 .
.
 .
.
4).
 .
.
24. Двойной интеграл в декартовых координатах. Определение, основные свойства.
1).
 ,
,
 .
2).
.
2).
 .
3).
.
3).
 .
4).
.
4).

 .
.
Если
f(x,y) в D:
f(
в D:
f( )
) - произведение представляет собой объем
цилиндрич. тела с основанием
,
образующие кот. || оси OZ
и кот. сверху ограничена частью пов-ти
= z(x,y).
Если эти построения выполнить для кажд.
площадки
,
то получим объем ступеньчатого тела,
кот. приближенно равен объему тела
снизу ограниченного обл. D,
сверху поверхностью z=f(x,y),
а с боков – цилиндрич. пов-тью образующая
кот. || оси OZ,
а направляющей служит граница области
D.
- произведение представляет собой объем
цилиндрич. тела с основанием
,
образующие кот. || оси OZ
и кот. сверху ограничена частью пов-ти
= z(x,y).
Если эти построения выполнить для кажд.
площадки
,
то получим объем ступеньчатого тела,
кот. приближенно равен объему тела
снизу ограниченного обл. D,
сверху поверхностью z=f(x,y),
а с боков – цилиндрич. пов-тью образующая
кот. || оси OZ,
а направляющей служит граница области
D.
Геометрич. чмысл: след-но уже ясно, что 2-ной интеграл дает объем тела, ограниченного областью D, поверхностью z=f(x,y), и поверхность с образующими || оси OZ.
Теорема: если f=z(x,y) непрерывна в замкнутой огран. обл. D, то существует и не зависит ни от сп. разбиения обл. D на части , ни от выбора точек в каждой части, этот предел и явл-ся 2-ным инт-ом от ф-ции f(x,y) на dxdy по области D.
Св-ва 2-го инт-ла:
1).
 .
.
2). .
.
3). .
.
25. Вычисление двойного интеграла в дск.
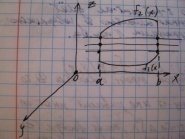 Вычисление
двойного инт-ла сводится к последоват.
вычислению 2-х опред. инт-ов. Пусть
требуется вычислить инт-л
Вычисление
двойного инт-ла сводится к последоват.
вычислению 2-х опред. инт-ов. Пусть
требуется вычислить инт-л
 ,
где ф-ция
,
где ф-ция
 непрерывна в обл. D.
непрерывна в обл. D.
Если
прямые || оси OX
пересек. гр. обл. D
не более, чем в 2-х точках, то эта обл.
наз-ся правильной
в направлении оси OX.
Аналогично опр-ся область правильная
в напр. оси OY.
Обл. правильная в напр. и той и др. оси
наз-ся правильной.
 .
Двойной инт-л=2-кратному инт-лу, в кот.
пределы интегрирования расставлены в
соответствии с заданием области D.
Если обл. D
не явл. правильной (в напрвлении хотя
бы 1-ой оси), то ее следует разбить на
неск. областей, из кот. явл. правильной.
.
Двойной инт-л=2-кратному инт-лу, в кот.
пределы интегрирования расставлены в
соответствии с заданием области D.
Если обл. D
не явл. правильной (в напрвлении хотя
бы 1-ой оси), то ее следует разбить на
неск. областей, из кот. явл. правильной.
26. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
Прежде всего рассмотрим вопрос о замене пер. в 2-ом инт-ле. – в ДСК. Если x=x(u,v) и y=y(u,v), то они определяют зависимость ДСК от криволин. корд. u,v. Предполагаем, что эти ф-ции имеют непрерывные частные производные по своим арг.
Якобиан:
 ,
тогда
,
тогда
 .
Будем рассматривать 2-ной инт-л в ПСК:
,
поэтому найдем для эт. случая Якобиан:
.
Будем рассматривать 2-ной инт-л в ПСК:
,
поэтому найдем для эт. случая Якобиан:
 .
Имеем 2-ой инт-л:
.
Имеем 2-ой инт-л:

 Порядок
инт-ния в эт. инт-ле выбирается произвольно.
Замечание:
к ПСК следует переходить, когда ф-ция
(под-ная) имеет более простой вид, чем
в ДСК.
Порядок
инт-ния в эт. инт-ле выбирается произвольно.
Замечание:
к ПСК следует переходить, когда ф-ция
(под-ная) имеет более простой вид, чем
в ДСК.
