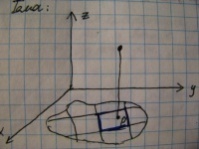
19. Дифференцирование неявных функций.
,
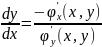определяет z
как функцию x,y.
,
,
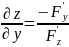если F
зависела от x,y,t,z
и определяла z
как неявную ф-цию арг-ов x,y,t,
то
мы бы нашли аналогичным образом.
20. Частные производные высших порядков.
Если
частные производные первого порядка
ф-ции u=f(
)
являются дифференцируемыми, то частными
производными 2-го порядка наз-ся
производная от ее частных производных
первого порядка. Обозначение:
и т.д. Аналогично определяются частные
производные порядка выше первого. Если
возникающие при многократном
дифференцировании «смешанные производные»
непрерывны, то рез-т не зависит от
порядка дифференцирования.
Дифференциалом
2-го порядка ф-ции наз. дифференциал от
дифференциала 1-го порядка, рассматриваемого
как ф-ция переменных при фиксированных
:
.
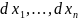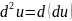Аналогично определяется дифференциал
3-го порядка и m-го
порядка:
.
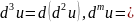
Дифференциал m-го
порядка ф-ции, где (
)
– независимые переменные, выражается
символич. ф-лой:
,
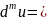
кот. формально раскрывается по
биномиальному закону, например, для
ф-ции двух независимых переменных
z=f(x,y)
имеем
,
.
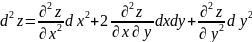21. Локальный экстремум функции двух аргументов.
z=z(z,y). т. ( ) наз-ся т. максимума этой ф-ции, если z( )>z(x,y), (x,y) – точка достаточно близкая к .
т.
наз-ся минимума ф-ции, если z(
)>z(x,y),для
всех точек (x,y);
достаточно близкая к (
).
Здесь и в дальнейшем мы полагаем, что ф-ция z рассм-ся в области ее определения D и все упоминаемые точки также берутся в области D. Предполагаем также z=z(x,y) дифференцируемая в кажд. точке обл. D (за исключением отдельных точек, где частные производные могутнее сущ-ть).
теорема
1: необходимый признак сущ-ния экстремума:
z=z(x,y)
достигает в т.М экстремума, то в т.М обе
производные:
равны 0 (или не сущ-ют). Точки, в кот.
частные производные =0 (или не сущ-ют)
наз-ся стационарными
точками
этой ф-ции.
теорема 2: достаточные условия сущ-ния экстремума: ф-ция z определена и непрерывна в обл. D. Пусть она такде в эт. обл. имеет нерпрер. частные производные до 3-го пор. включительно и пусть ( ) есть стацион. точка. Тогда:
I).
,
max AC-
>0,
A<0
II). , min AC- >0, A>0
III).
,
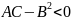нет экстремума.
Из
критерия Сильвестра:
,
,
,
.
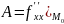22. Условный экстремум. Метод множителей Лагранжа.
z=f(x,y),
причем аргументы x,y
связаны нек. соотношением:
(2). Требуется найти экстремум функции
z,
кот. в данном случае наз-ся условным
экстремумом.
Естейственно, что ф-ция z
рассм-ся в нек. обл. D,
где сама ф-ция и ее производные непрерывны;
это же относится и к ф-ции
.
(3).
Продифференцировав 2 по арг. x
как ф-цию зад. неявно:
(4). Умножим обе части ур. 4 на нек. неизв.
множитель
и сложим с ур. 3 (и приведем подобные
члены):
(5). Подберем λ т.о., чтобы 2-ая ск. рав-ва
5 обратилась в 0.
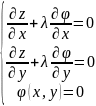,(6)
тогда необходимо, чтобы и 1-я ск. 5
в 0, учтем, что есть ур. 2. Решаем сист. и
нах. λ. После того как нашли λ, найдем
пары значений (x,y):
это и будут стационарные
точки данной ф-ции.
Итак, найдя пары значений (x,y)
мы определим лишь стац. т-ки, т.е. т-ки в
кот. вып-ся необх. условие сущ-ния
экстремума. Что касается достаточных
условий сущ-ния экстремума, то их нет
и вопрос о сущ-нии экстремумов реш-ся
из нек. доп. соображений по отношению
к кажд. задаче.
Заметим,
что левые части системы (6) есть частные
производные по переменным x,y,λ
от ф-ции
(7). Эта
ф-ция F
наз-ся ф-цией Лагранжа, а множитель λ –
множитель Лагранжа. Замечание:
для наших целей сомножитель λ имеет
только вспом. роль и после того как
найдены стацион. т-ки, он больше не
нужен.
Пример:
Составим
ф-цию Лагранжа: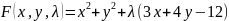
.
,
,
подставляем в 1 и 3:
,
(
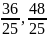)-стац.
точка. Подставим
в ф-цию z:
.
;
.
.