
- •1). Первообразная и неопределённый интеграл. Таблица основных неопределённых интегралов.
- •2).Замена переменной и интегрирование по частям под знаком неопределённого интеграла.
- •6). Интегралы вида: , .
- •7). Интегралы вида: .
- •10). Понятие определённого интеграла, основные свойства определённого интеграла, его вычисление.
- •11.Вычисление площадей плоских фигур, объёмов тел и длин дуг с помощью определённого интеграла.
- •11’.Интегрирование по частям и замена переменной под знаком определённого интеграла.
- •12. Несобственные интегралы 1-го рода.
- •13. Несобственные интегралы 2-го рода.
- •14. Понятие функции нескольких переменных. Предел в точке, непрерывность.
- •15. Частные производные функции двух аргументов, их геометрический смысл.
- •16. Полный дифференциал функции двух и трёх переменных.
- •17. Производные сложной функции нескольких аргументов.
- •19. Дифференцирование неявных функций.
- •20. Частные производные высших порядков.
- •21. Локальный экстремум функции двух аргументов.
- •22. Условный экстремум. Метод множителей Лагранжа.
- •23. Наименьшее и наибольшее значения функции двух аргументов в замкнутой области.
- •24. Двойной интеграл в декартовых координатах. Определение, основные свойства.
- •25. Вычисление двойного интеграла в дск.
- •26. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •27. Вычисление площадей и объёмов с помощью двойного интеграла.
- •28. Тройной интеграл. Определение, основные свойства. Его вычисление в декартовых координатах.
- •29. Цилиндрические координаты. Тройной интеграл в цилиндрических координатах.
- •30. Сферические координаты. Тройной интеграл в сферических координатах.
- •31. Криволинейный интеграл 1-го рода, его свойства и вычисление.
- •32. Криволинейный интеграл 2-го рода, его определение, свойства и вычисление.
- •33. Криволинейный интеграл 2-го рода как работа переменной силы на криволинейном пути.
- •34. Вычисление площади плоской фигуры с помощью кри-2.
- •35. Формула Грина.
- •36. Независимость криволинейного интеграла от пути интегрирования. Нахождение функции по её полному дифференциалу.
- •37. Поверхностный интеграл 1-го рода, его свойства и вычисление. Поверхностный интеграл 2-го рода.
- •38. Вычисление массы поверхности.
- •39. Скалярное поле, производная по направлению.
- •40. Градиент.
- •41. Векторное поле. Дивергенция.
- •42. Поток векторного поля.
- •43. Формула Остроградского.
- •44. Формула Стокса.
- •45. Оператор Гамильтона.
- •46. Оператор Лапласа.
- •47. Потенциальное векторное поле и его свойства.
- •48. Соленоидальное векторное поле.
- •49. Гармоническое векторное поле.
15. Частные производные функции двух аргументов, их геометрический смысл.
Если
ф-ция z=f(x,y)
определена в нек. области D,
тогда частное приращение
 .
Частная производная (1-го порядка)
называется предел отношения частного
приращения к приращению аргумента:
.
Частная производная (1-го порядка)
называется предел отношения частного
приращения к приращению аргумента:
 .
.
Геометрический
смысл производных:
частная производная ф-ции z=f(x,y)
по х в т.(
)
равна тангенсу угла с осью ОХ касательной
к кривой, получаемой при пересечении
с повехностью
плоскости
,
 ,
аналогично
,
аналогично
 .
.
16. Полный дифференциал функции двух и трёх переменных.
Запишем
выр. для полного приращения z=f(x,y):
 .
В пра. части равенства прибавим и отнимем
.
В пра. части равенства прибавим и отнимем
 :
:

Преобразуем кажд. скобку используя т.Лагранжа:
1).
 ,
,
 -т.ка
между y
и
-т.ка
между y
и
 .
.
2). ,
,
 -т.ка
между x
и
-т.ка
между x
и
 .
.
 рассматривая
это равенство и беря предел обеих его
частей при
рассматривая
это равенство и беря предел обеих его
частей при
 и
и
 получим:
получим:
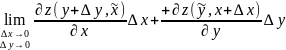 .
Используя теорему о том, что если ф-ция
имеет предел, то она отличается от
предела на величину б.м. Тогда мы получим,
что
.
Используя теорему о том, что если ф-ция
имеет предел, то она отличается от
предела на величину б.м. Тогда мы получим,
что

 ,
- б.м.в.
,
- б.м.в.
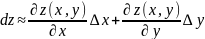 ,
,
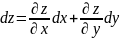 .
Если ф-ция была большего числа пер.
z=z(x,y,u):
.
Если ф-ция была большего числа пер.
z=z(x,y,u):
 .
.
 -главная
часть приращения ф-ции. Как и в случае
ф-ции одного арг. дифференциал f(x,y)
есть главная часть приращения этой
ф-ции. След-но в
-главная
часть приращения ф-ции. Как и в случае
ф-ции одного арг. дифференциал f(x,y)
есть главная часть приращения этой
ф-ции. След-но в
 вычислениях можно полное приращение
ф-ции заменять на ее дифференциал.
вычислениях можно полное приращение
ф-ции заменять на ее дифференциал.
17. Производные сложной функции нескольких аргументов.
Пусть
задана непрерывно дифференц. ф-ция
u=f(x,y,z),
где в свою очередь x=x(t),
y=y(t),
z=z(t)
являются непрерывно дифференцируемыми
ф-циями переменной t.
Тем самым определена сложная ф-ция
u=f(x(t),y(t),z(t))
одной переменной t.
Найдем производную этой ф-ции в т.t.
Для этого придадим переменной t
приращение
 .
Оно вызовет приращения ф-ции
.
Оно вызовет приращения ф-ции
 ,
причем при
,
причем при
 таже
таже
 в силу дифференцируемости ф-ции
в силу дифференцируемости ф-ции
 .
В силу дифференцируемости ф-ции
u=f(x,y,z)
ее полное приращение
.
В силу дифференцируемости ф-ции
u=f(x,y,z)
ее полное приращение
 в точке
в точке
 :
:
 ,
где
,
где
 ,
а частные производные
,
а частные производные
 вычислены в точке (x(t),y(t),z(t)).
Разделив все члены равенства (1) на
и перейдя в полученном выражении к
пределу при
в силу дифференцируемости ф-ций x,y,z
по переменной t,
получим:
вычислены в точке (x(t),y(t),z(t)).
Разделив все члены равенства (1) на
и перейдя в полученном выражении к
пределу при
в силу дифференцируемости ф-ций x,y,z
по переменной t,
получим:
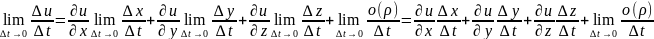 .
Покажем, что
.
Покажем, что
 .
В самом деле:
.
В самом деле:
 .
Т.о, окончательно равенство примет вид:
.
Т.о, окончательно равенство примет вид:
 или
или
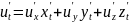 .
Эти рав-ва часто наз-ют цепочным
правилом дифференцирования сложной
ф-ции.
.
Эти рав-ва часто наз-ют цепочным
правилом дифференцирования сложной
ф-ции.
18. Полная производная+ур. кас. и нормали.
Пусть
u=f(z,y,z),
где y=y(x),
z=z(x).
Найдем
 .
Используя ф-лу
,
при t=x,
получаем:
.
Используя ф-лу
,
при t=x,
получаем:
 - это формула
полной производной.
Пусть теперь задана непрерывно
дифференцируемая ф-ция u=f(x,y,z),
где в свою очередь x=x(s,t),
y=y(s,t),
z=z(s,t)
– непрерывно дифференцируемые ф-ции
переменных s,t.
Тем самым определена сложная ф-ция
u=f(x(s,t),y(s,t),z(s,t))=
- это формула
полной производной.
Пусть теперь задана непрерывно
дифференцируемая ф-ция u=f(x,y,z),
где в свою очередь x=x(s,t),
y=y(s,t),
z=z(s,t)
– непрерывно дифференцируемые ф-ции
переменных s,t.
Тем самым определена сложная ф-ция
u=f(x(s,t),y(s,t),z(s,t))= двух переменных s,t.
Получим ф-лу для вычисления ее частных
производных. Т.к. при вычислении ее
частных производных ф-ции
одна из переменных фиксируется, то этот
случай по сути дела сводится к
рассмотренному выше и, согласно
,
ф-лы для вычисления частных производных
двух переменных s,t.
Получим ф-лу для вычисления ее частных
производных. Т.к. при вычислении ее
частных производных ф-ции
одна из переменных фиксируется, то этот
случай по сути дела сводится к
рассмотренному выше и, согласно
,
ф-лы для вычисления частных производных
 и
и
 :
:
 ;
;
 .
.
Касательная
плоскость и нормаль к поверхности:
касательная
плоскость к пов-ти z=f(x,y)
в т.
и содержащая касательные, проведенные
ко всем кривым, лежащим на пов-ти и
проходящим через т.
.
Нормаль
– перпендик.
к касат. плоскости в этой точке
.
Уравнение касс. к плоскости, если пов-ть
была задана в явном виде, то:
 .
Если ур. пов-ти было задано в неявной
ф-ме:
.
Если ур. пов-ти было задано в неявной
ф-ме:
 .
.
Ур-ния
нормали для кажд. способа задания
пов-ти:
 ,
,
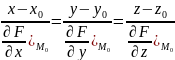 .
.
