
- •1). Первообразная и неопределённый интеграл. Таблица основных неопределённых интегралов.
- •2).Замена переменной и интегрирование по частям под знаком неопределённого интеграла.
- •6). Интегралы вида: , .
- •7). Интегралы вида: .
- •10). Понятие определённого интеграла, основные свойства определённого интеграла, его вычисление.
- •11.Вычисление площадей плоских фигур, объёмов тел и длин дуг с помощью определённого интеграла.
- •11’.Интегрирование по частям и замена переменной под знаком определённого интеграла.
- •12. Несобственные интегралы 1-го рода.
- •13. Несобственные интегралы 2-го рода.
- •14. Понятие функции нескольких переменных. Предел в точке, непрерывность.
- •15. Частные производные функции двух аргументов, их геометрический смысл.
- •16. Полный дифференциал функции двух и трёх переменных.
- •17. Производные сложной функции нескольких аргументов.
- •19. Дифференцирование неявных функций.
- •20. Частные производные высших порядков.
- •21. Локальный экстремум функции двух аргументов.
- •22. Условный экстремум. Метод множителей Лагранжа.
- •23. Наименьшее и наибольшее значения функции двух аргументов в замкнутой области.
- •24. Двойной интеграл в декартовых координатах. Определение, основные свойства.
- •25. Вычисление двойного интеграла в дск.
- •26. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •27. Вычисление площадей и объёмов с помощью двойного интеграла.
- •28. Тройной интеграл. Определение, основные свойства. Его вычисление в декартовых координатах.
- •29. Цилиндрические координаты. Тройной интеграл в цилиндрических координатах.
- •30. Сферические координаты. Тройной интеграл в сферических координатах.
- •31. Криволинейный интеграл 1-го рода, его свойства и вычисление.
- •32. Криволинейный интеграл 2-го рода, его определение, свойства и вычисление.
- •33. Криволинейный интеграл 2-го рода как работа переменной силы на криволинейном пути.
- •34. Вычисление площади плоской фигуры с помощью кри-2.
- •35. Формула Грина.
- •36. Независимость криволинейного интеграла от пути интегрирования. Нахождение функции по её полному дифференциалу.
- •37. Поверхностный интеграл 1-го рода, его свойства и вычисление. Поверхностный интеграл 2-го рода.
- •38. Вычисление массы поверхности.
- •39. Скалярное поле, производная по направлению.
- •40. Градиент.
- •41. Векторное поле. Дивергенция.
- •42. Поток векторного поля.
- •43. Формула Остроградского.
- •44. Формула Стокса.
- •45. Оператор Гамильтона.
- •46. Оператор Лапласа.
- •47. Потенциальное векторное поле и его свойства.
- •48. Соленоидальное векторное поле.
- •49. Гармоническое векторное поле.
13. Несобственные интегралы 2-го рода.
Есть
ф-ция f(x),
заданная в конечном промежутке [a,b].
Необходимым условием сущ-ния опред.
инт-ла:
 явл-ся ограниченность ф-ции f(x)
на отрезке [a,b].
Пусть ф-ция определена на промеж-ке
[a,b)
и не ограничена при
явл-ся ограниченность ф-ции f(x)
на отрезке [a,b].
Пусть ф-ция определена на промеж-ке
[a,b)
и не ограничена при
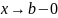 ,
т.е.
,
т.е.
 .
Точка b
при этом – особая
для
f(x).
В этом случае говорят, что f(x)
имеет
особенность в точке x=b.
Будем считать, что для любого
.
Точка b
при этом – особая
для
f(x).
В этом случае говорят, что f(x)
имеет
особенность в точке x=b.
Будем считать, что для любого
 ф-ция f(x)
интегрируема на отрезке [a,b-
ф-ция f(x)
интегрируема на отрезке [a,b- ],
т.е. сущ-ет инт-л
],
т.е. сущ-ет инт-л
 ,
если сущ-ет конечный предел:
,
если сущ-ет конечный предел:
 ,
то он наз-ся НСИ2 на промеж. [a,b)
и обозначается
,
то он наз-ся НСИ2 на промеж. [a,b)
и обозначается
 .
Аналогично, если ф-ция f(x)
имеет особенность в точке x=a,
то:
.
Аналогично, если ф-ция f(x)
имеет особенность в точке x=a,
то:
 .
Если особой точкой явтл-ся точка c,
a<c<b,
то:
.
Если особой точкой явтл-ся точка c,
a<c<b,
то:
 .
НСИ2 сходящийся, если существует конечный
предел. В противном случае наз-ся
расходящимся. Геометрически сходимость
НСИ2 означает, что фигура, ограниченная
кривой y=f(x),
прямыми x=a,
x=b,
беск. вытянутая в направлении оси Y
при x
.
НСИ2 сходящийся, если существует конечный
предел. В противном случае наз-ся
расходящимся. Геометрически сходимость
НСИ2 означает, что фигура, ограниченная
кривой y=f(x),
прямыми x=a,
x=b,
беск. вытянутая в направлении оси Y
при x ,
или при
,
или при
 ,
или при
,
или при
 ,
имеет беск. площадь S.
,
имеет беск. площадь S.
 ,
,

14. Понятие функции нескольких переменных. Предел в точке, непрерывность.
 Если
каждой паре чисел x,y
(взятых в опред. порядке) отвечает вполне
определенное значение переменной z,
то: z=f(x,y)
– ф-ция 2-х переменных. Множество пар
значений при кот. аналитич. выражение
имеет смысл, наз-ся областью
опред. ф-ции z.
Если
каждой паре чисел x,y
(взятых в опред. порядке) отвечает вполне
определенное значение переменной z,
то: z=f(x,y)
– ф-ция 2-х переменных. Множество пар
значений при кот. аналитич. выражение
имеет смысл, наз-ся областью
опред. ф-ции z.
Если эти построения вып-ть для кажд. точки (x,y) из обл. опред., то точки P будут лежать на нек. пов-ти, кот. и явл-ся графиком ф-ции z=f(x,y). Если точки границы области принадлежат самой области, то она наз-ся замкнутой, если же точки границы самой области не принадлежит, то область наз-ся открытой. Область наз-ся ограниченнойЮ если сущ-ет такое полож. число а, что расстояние люб. точки обл. до начала координат не превосходит этого числа.
u=f(x,y,z) – график ф-ции 3-х и > числа переменных построить нельзя.
Линии и поверхности уровня: z=f(x,y). Линией уровня этой ф-ции наз-ся линия с уровнем: f(x,y)=c, z=c,c=const.
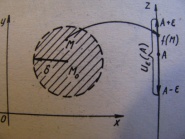 u=f(x,y,z)
поверхности ур-ня этой ф-ции это пов-ти
с ур-ем: f(x,y,z)=C,
u=C=const.
Пример:
u=f(x,y,z)
поверхности ур-ня этой ф-ции это пов-ти
с ур-ем: f(x,y,z)=C,
u=C=const.
Пример:
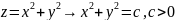 – семейство окружностей с центром в
н.коорд. с радиусом
– семейство окружностей с центром в
н.коорд. с радиусом
 .
.
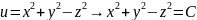 :
1. C>0:
:
1. C>0:
 – однополостный гиперболоид. 2. C<0-
2-полостный гиперболоид. 3.
– однополостный гиперболоид. 2. C<0-
2-полостный гиперболоид. 3. –семейство конусов.
–семейство конусов.
 Предел
ф-ции в точке: пусть
ф-ция z=f(x,y)
определена в нек. проколотой окрестности
точки
Предел
ф-ции в точке: пусть
ф-ция z=f(x,y)
определена в нек. проколотой окрестности
точки
 .
Число А наз-ся пределом ф-ции f
в точке
.
Число А наз-ся пределом ф-ции f
в точке
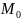 ,
если для любого
можно указать
,
если для любого
можно указать
 ,
такое что, для всех точек M=(x,y)
точки
выполняется неравенство
,
такое что, для всех точек M=(x,y)
точки
выполняется неравенство
 .
Если число А – предел ф-ции f(x,y)
в точке
.
Если число А – предел ф-ции f(x,y)
в точке
 ,
то этот факт будем записывать в виде
,
то этот факт будем записывать в виде
 .
.
Повторный
предел:
определение предела ф-ции
 в точке (
в точке ( )
предполагает, что х стремится к
)
предполагает, что х стремится к
 независимо от стремления y
к
независимо от стремления y
к
 ,
необходимо лишь, чтобы точка
,
необходимо лишь, чтобы точка
 принадлежала области определения D(f)
ф-ции z.
Если зафиксировать пер-ную y,
то ф-ция f(x,y)
становится ф-цией одной переменной х,
где
принадлежала области определения D(f)
ф-ции z.
Если зафиксировать пер-ную y,
то ф-ция f(x,y)
становится ф-цией одной переменной х,
где
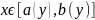 .
Можно поставить вопрос о существовании
предела
.
Можно поставить вопрос о существовании
предела
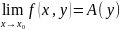 ,
кот. является ф-цией от y.
Предельный переход означает, что т.М
по прямой y=const
стремится к т.
,
кот. является ф-цией от y.
Предельный переход означает, что т.М
по прямой y=const
стремится к т.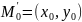 .
Затем можно поставить вопрос о сущ-нии
предела
.
Затем можно поставить вопрос о сущ-нии
предела
 ,
кот. наз-ся повторным
пределом.
Предельный переход означает, что т.
,
кот. наз-ся повторным
пределом.
Предельный переход означает, что т. по прямой x=
.
Аналогично вводится повторный предел:
по прямой x=
.
Аналогично вводится повторный предел:
 ,
где
,
где
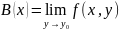 .
Предельный переход означает, что вначале
точка М стремится к точке
.
Предельный переход означает, что вначале
точка М стремится к точке
 по прямой x=const,
а затем т.
по прямой x=const,
а затем т. стремится к
по прямой
стремится к
по прямой
 .
Итак повторные пределы отражают факт
стремления переменной точки М=(x,y)
к точке
по сторонам прямоугольника
.
Итак повторные пределы отражают факт
стремления переменной точки М=(x,y)
к точке
по сторонам прямоугольника
 ,
параллельным координатным осям.
,
параллельным координатным осям.
Непрерывность
ф-ции многих переменных: ф-ция
z=f(x,y)
наз-ся непрерывной, если ее предел в
точке
равен значению ф-ции в этой точке, т.е.
если
 .
.
