
- •1). Первообразная и неопределённый интеграл. Таблица основных неопределённых интегралов.
- •2).Замена переменной и интегрирование по частям под знаком неопределённого интеграла.
- •6). Интегралы вида: , .
- •7). Интегралы вида: .
- •10). Понятие определённого интеграла, основные свойства определённого интеграла, его вычисление.
- •11.Вычисление площадей плоских фигур, объёмов тел и длин дуг с помощью определённого интеграла.
- •11’.Интегрирование по частям и замена переменной под знаком определённого интеграла.
- •12. Несобственные интегралы 1-го рода.
- •13. Несобственные интегралы 2-го рода.
- •14. Понятие функции нескольких переменных. Предел в точке, непрерывность.
- •15. Частные производные функции двух аргументов, их геометрический смысл.
- •16. Полный дифференциал функции двух и трёх переменных.
- •17. Производные сложной функции нескольких аргументов.
- •19. Дифференцирование неявных функций.
- •20. Частные производные высших порядков.
- •21. Локальный экстремум функции двух аргументов.
- •22. Условный экстремум. Метод множителей Лагранжа.
- •23. Наименьшее и наибольшее значения функции двух аргументов в замкнутой области.
- •24. Двойной интеграл в декартовых координатах. Определение, основные свойства.
- •25. Вычисление двойного интеграла в дск.
- •26. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •27. Вычисление площадей и объёмов с помощью двойного интеграла.
- •28. Тройной интеграл. Определение, основные свойства. Его вычисление в декартовых координатах.
- •29. Цилиндрические координаты. Тройной интеграл в цилиндрических координатах.
- •30. Сферические координаты. Тройной интеграл в сферических координатах.
- •31. Криволинейный интеграл 1-го рода, его свойства и вычисление.
- •32. Криволинейный интеграл 2-го рода, его определение, свойства и вычисление.
- •33. Криволинейный интеграл 2-го рода как работа переменной силы на криволинейном пути.
- •34. Вычисление площади плоской фигуры с помощью кри-2.
- •35. Формула Грина.
- •36. Независимость криволинейного интеграла от пути интегрирования. Нахождение функции по её полному дифференциалу.
- •37. Поверхностный интеграл 1-го рода, его свойства и вычисление. Поверхностный интеграл 2-го рода.
- •38. Вычисление массы поверхности.
- •39. Скалярное поле, производная по направлению.
- •40. Градиент.
- •41. Векторное поле. Дивергенция.
- •42. Поток векторного поля.
- •43. Формула Остроградского.
- •44. Формула Стокса.
- •45. Оператор Гамильтона.
- •46. Оператор Лапласа.
- •47. Потенциальное векторное поле и его свойства.
- •48. Соленоидальное векторное поле.
- •49. Гармоническое векторное поле.
42. Поток векторного поля.
Пусть вект. поле образовано вектором . Представим, что нек. пов-ть S нах-ся в потоке и пропускает жикость. Подсчитаем кол-во жидк., кот. протекает через пов-ть S.
Выберем
опред сторону пов-ти S.
пусть
 - единичный вектор нормали к рассматриваемой
стороне пов-ти S.
Разобьем пов-ть на эл-ные площ-ки
.
Выберем в кажд. площ-ке т.
- единичный вектор нормали к рассматриваемой
стороне пов-ти S.
Разобьем пов-ть на эл-ные площ-ки
.
Выберем в кажд. площ-ке т.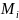 и вычислим зн-ния вектора скор.
и вычислим зн-ния вектора скор.
 в кажд. точке. Будем приближенно считать
кажд. площ-ку плоской, а
пост. по модулю и одинаково направленным
в кажд. т-ке площ-ки. Тогда за ед. вр.
через
протекает кол-во жидк.,
в кажд. точке. Будем приближенно считать
кажд. площ-ку плоской, а
пост. по модулю и одинаково направленным
в кажд. т-ке площ-ки. Тогда за ед. вр.
через
протекает кол-во жидк.,
 ,
где
- площ. i-ой
площ-ки,
,
где
- площ. i-ой
площ-ки,
 - высота i-ого
цилиндра с образующей
- высота i-ого
цилиндра с образующей
 .
Но
явл-ся проекцией
на нормаль
.
Но
явл-ся проекцией
на нормаль
 :
:
 =
= ,
- единичный вектор нормали к пов-ти в
т.
.
След-но, общее кол-во жидк., протекающее
через всю пов-ть S
за ед. вр., найдем вычислив сумму
,
- единичный вектор нормали к пов-ти в
т.
.
След-но, общее кол-во жидк., протекающее
через всю пов-ть S
за ед. вр., найдем вычислив сумму
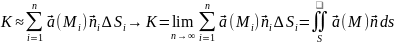 .
.
Независимо от физ. смысла поля полученный инт-л наз-ют потоком вект. поля.
Потоком
вект. поля
через
пов-ть S
– инт-л по пов-ти от скал. произв. вектора
поля на ед. вектор нормали к поверхности,
т.е.:
 .
.
Т.к.
 ,
где
,
где
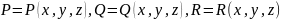 - проекции вектора
на соответств. коорд. оси, то поток
вектора:
- проекции вектора
на соответств. коорд. оси, то поток
вектора:
 .
Поток К вектора
есть скал. вел-на. Вел-на К = объему жидк.,
кот. протекает через пов-ть S
за ед. вр. В этом состоит физ .смысл
потока.
.
Поток К вектора
есть скал. вел-на. Вел-на К = объему жидк.,
кот. протекает через пов-ть S
за ед. вр. В этом состоит физ .смысл
потока.
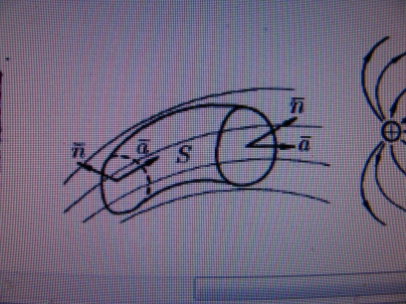 Случай,
когда
пов-ть замкн. и огран-ет нек. объем V.
Тогда поток вектора запис-ся:
Случай,
когда
пов-ть замкн. и огран-ет нек. объем V.
Тогда поток вектора запис-ся:
 .
В эт. случае за напр. вектора
.
В эт. случае за напр. вектора
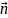 обычно берут напр. внешней нормали и
говорят о потоке изнутри пов-ти S.
Если вект. поле
обычно берут напр. внешней нормали и
говорят о потоке изнутри пов-ти S.
Если вект. поле
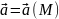 есть поле скоростей текущей жидкости,
то величина потока К через замкн. пов-ть
дает разность между кол-ом жидк-ти,
вытек-щей из обл. V
и втекающей в нее в ед. вр. (в точках
пов-ти S,
где вект. линии выходят из объема V,
внешняя нормаль образует с вект-ом
острый угол и
есть поле скоростей текущей жидкости,
то величина потока К через замкн. пов-ть
дает разность между кол-ом жидк-ти,
вытек-щей из обл. V
и втекающей в нее в ед. вр. (в точках
пов-ти S,
где вект. линии выходят из объема V,
внешняя нормаль образует с вект-ом
острый угол и
 ;
в точках, где вект. линии входят в объем,
;
в точках, где вект. линии входят в объем,
 ).
).
При этом если K>0, то из обл-ти V вытекает больше жидкости, чем в нее втекает. Это озн-ет, что внутри обл. имеются доп. ист-ки. Если К<0, то внутри обл. V есть стоки, поглощающие избыток жидкости. Если К=0, то из обл. V вытекает столько же жидк., сколько в нее втекает в ед. вр.; внутри обл. либо нет ни ист-ов, ни ст-ов, либо они таковы, что их действие взаимно компенсируется.
Пример:
найти поток вект-ра
 через верхнюю сторону треугольника,
полученного при перес-нии плоскости
3x+6y-2z-6=0
с коорд. плоскостями.Решение:
через верхнюю сторону треугольника,
полученного при перес-нии плоскости
3x+6y-2z-6=0
с коорд. плоскостями.Решение:
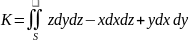 .
Нормаль к верхней стороне треуг. образует
с осью Ox
тупой угол, Oy
– тупой, Oz
– острый.
.
Нормаль к верхней стороне треуг. образует
с осью Ox
тупой угол, Oy
– тупой, Oz
– острый.
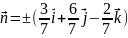 ,
на верхней стороне
,
на верхней стороне
 ,
поэтому надо выбрать знак -; получим:
,
поэтому надо выбрать знак -; получим:
 .
Итак,
.
Итак,
 .
Находим их:
.
Находим их:
 .
.
 .
.
 .
.
 .
.
43. Формула Остроградского.
Используя
понятия потока и дивергенции вект.
поля, запишем ф-лу Остроградского-Гаусса:
 .
Рассматривая обл. V,
ограниченную замкн. пов-тью S,
в вект. поле
,
можно утв-ть, что левая часть ф-лы
Остроградского есть поток вектора
через пов-ть S;
подынтегр. ф-ция правой чати ф-лы есть
дивергенция вектора
.
След-но ф-ла
Остроградского
может выглядеть так:
.
Рассматривая обл. V,
ограниченную замкн. пов-тью S,
в вект. поле
,
можно утв-ть, что левая часть ф-лы
Остроградского есть поток вектора
через пов-ть S;
подынтегр. ф-ция правой чати ф-лы есть
дивергенция вектора
.
След-но ф-ла
Остроградского
может выглядеть так:
 (встречается
чаще всего). Ф-ла Остроградского-Гаусса
означает, что поток
вект. поля через замкн. пов-ть S
(в напр. внешней нормали, т.е. изнутри)
равен 3-ому инт-лу от див. этого поля по
объему V,
ограниченному данной пов-тью.
Используя ф-лу
, можно дать другое определение
дивергенции вект. поля
в точке М.
(встречается
чаще всего). Ф-ла Остроградского-Гаусса
означает, что поток
вект. поля через замкн. пов-ть S
(в напр. внешней нормали, т.е. изнутри)
равен 3-ому инт-лу от див. этого поля по
объему V,
ограниченному данной пов-тью.
Используя ф-лу
, можно дать другое определение
дивергенции вект. поля
в точке М.
По
теореме о среднем для 3-ного инт-ла
имеем:
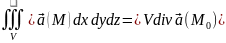 ,
– нек. (средняя) точка области V.
Тогда ф-лу можно переписать:
,
– нек. (средняя) точка области V.
Тогда ф-лу можно переписать:
 .
Тогда:
.
Тогда:
 .
Пусть пов-ть S
стягивается в точку. Тогда
.
Пусть пов-ть S
стягивается в точку. Тогда
 и мы получим выр-ние для
и мы получим выр-ние для
 в точке М:
в точке М:
 .
.
