
- •1). Первообразная и неопределённый интеграл. Таблица основных неопределённых интегралов.
- •2).Замена переменной и интегрирование по частям под знаком неопределённого интеграла.
- •6). Интегралы вида: , .
- •7). Интегралы вида: .
- •10). Понятие определённого интеграла, основные свойства определённого интеграла, его вычисление.
- •11.Вычисление площадей плоских фигур, объёмов тел и длин дуг с помощью определённого интеграла.
- •11’.Интегрирование по частям и замена переменной под знаком определённого интеграла.
- •12. Несобственные интегралы 1-го рода.
- •13. Несобственные интегралы 2-го рода.
- •14. Понятие функции нескольких переменных. Предел в точке, непрерывность.
- •15. Частные производные функции двух аргументов, их геометрический смысл.
- •16. Полный дифференциал функции двух и трёх переменных.
- •17. Производные сложной функции нескольких аргументов.
- •19. Дифференцирование неявных функций.
- •20. Частные производные высших порядков.
- •21. Локальный экстремум функции двух аргументов.
- •22. Условный экстремум. Метод множителей Лагранжа.
- •23. Наименьшее и наибольшее значения функции двух аргументов в замкнутой области.
- •24. Двойной интеграл в декартовых координатах. Определение, основные свойства.
- •25. Вычисление двойного интеграла в дск.
- •26. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •27. Вычисление площадей и объёмов с помощью двойного интеграла.
- •28. Тройной интеграл. Определение, основные свойства. Его вычисление в декартовых координатах.
- •29. Цилиндрические координаты. Тройной интеграл в цилиндрических координатах.
- •30. Сферические координаты. Тройной интеграл в сферических координатах.
- •31. Криволинейный интеграл 1-го рода, его свойства и вычисление.
- •32. Криволинейный интеграл 2-го рода, его определение, свойства и вычисление.
- •33. Криволинейный интеграл 2-го рода как работа переменной силы на криволинейном пути.
- •34. Вычисление площади плоской фигуры с помощью кри-2.
- •35. Формула Грина.
- •36. Независимость криволинейного интеграла от пути интегрирования. Нахождение функции по её полному дифференциалу.
- •37. Поверхностный интеграл 1-го рода, его свойства и вычисление. Поверхностный интеграл 2-го рода.
- •38. Вычисление массы поверхности.
- •39. Скалярное поле, производная по направлению.
- •40. Градиент.
- •41. Векторное поле. Дивергенция.
- •42. Поток векторного поля.
- •43. Формула Остроградского.
- •44. Формула Стокса.
- •45. Оператор Гамильтона.
- •46. Оператор Лапласа.
- •47. Потенциальное векторное поле и его свойства.
- •48. Соленоидальное векторное поле.
- •49. Гармоническое векторное поле.
40. Градиент.
Вектор,
указывающий направление
,
в кот. производная
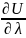 имеет наибольшее значение, наз-ся
градиентом.
Вектор, координатами кот. явл. значения
частных производных ф-ции U(x,y,z)
в точке M(x,y,z),
наз-ют градиентом
ф-ции
и обозначают grad
U,
т.е.
имеет наибольшее значение, наз-ся
градиентом.
Вектор, координатами кот. явл. значения
частных производных ф-ции U(x,y,z)
в точке M(x,y,z),
наз-ют градиентом
ф-ции
и обозначают grad
U,
т.е.

 .
Отметим, что grad
U
есть вект. величина. Говорят: скал. поле
U
продолжает вект. поле градиента U.
Теперь равенство
можно записать в виде:
.
Отметим, что grad
U
есть вект. величина. Говорят: скал. поле
U
продолжает вект. поле градиента U.
Теперь равенство
можно записать в виде:
 ,
,
 ,
- угол между вектором grad
U
и направлением
.
Из последней ф-лы следует, что произв.
по напр. достигает наиб. значения, когда
,
- угол между вектором grad
U
и направлением
.
Из последней ф-лы следует, что произв.
по напр. достигает наиб. значения, когда
 ,
т.е.
,
т.е.
 .
Т.о., направление град. совпадает с напр.
,
вдоль которого ф-ция (поле) меняется
быстрее всего, т.е. градиент
ф-ции указывает направление наибыстрейшего
возрастаня ф-ции.
Наибольшая скор. изменения ф-ции U
в точке М равна:
.
Т.о., направление град. совпадает с напр.
,
вдоль которого ф-ция (поле) меняется
быстрее всего, т.е. градиент
ф-ции указывает направление наибыстрейшего
возрастаня ф-ции.
Наибольшая скор. изменения ф-ции U
в точке М равна:
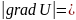
 .
В этом сосотоит физ. смысл градиента.
.
В этом сосотоит физ. смысл градиента.
Св-ва
градиента ф-ции:
1.град.
направлен по нормали к пов-ти кровня,
проходящей через данную
точку.2.grad(U+V)=gradU+gradV.
3.grad(cU)=cgradU,
c=const.4.grad(UV)=UgradV+VgradU.
5.grad .
6.
.
6.
 .
.
Замечание: эти св-ва градиента ф-ции справедливы и для плоского поля.
41. Векторное поле. Дивергенция.
Если
каждой точке точке М области простр-ва
соответствует нек. вектор
 ,
то говорят, что задано векторное
поле.
Векторная
линия – линия,
касательная к которой в кажд. ее точке
М имеет напр. соответствующего ей
вектора
,
то говорят, что задано векторное
поле.
Векторная
линия – линия,
касательная к которой в кажд. ее точке
М имеет напр. соответствующего ей
вектора
 .
Векторная
трубка – совокупность
всех вект. линий поля, проходящих через
нек. замкнутую кривую. Изучение вект.
поля обычно начинают с изучения
расположения его вект. линий. Векторные
линии поля
.
Векторная
трубка – совокупность
всех вект. линий поля, проходящих через
нек. замкнутую кривую. Изучение вект.
поля обычно начинают с изучения
расположения его вект. линий. Векторные
линии поля
 описываются сист. дифф. ур-ний вида
описываются сист. дифф. ур-ний вида
 .
Действительно, пусть PQ
– векторная линия поля,
.
Действительно, пусть PQ
– векторная линия поля,
 – ее радиус-вектор. Тогда вектор
– ее радиус-вектор. Тогда вектор
 направлен по касательной к линии PQ
в точке М. В силу коллинеарности векторов
направлен по касательной к линии PQ
в точке М. В силу коллинеарности векторов
 и
и
 следует пропорциональность их проекций,
т.е.:
.
следует пропорциональность их проекций,
т.е.:
.
Дивергенция
(расходимость) – характеристика вект-го
поля, определяющая распределение и
интенсивность источников и стоков
поля: дивергенцией
 в точке М наз-ся скаляр вида
в точке М наз-ся скаляр вида
 и обозначается:
и обозначается:

Св-ва
дивергенции:
1.если
- пост. вектор, то
 .
.
2. ,
где с=const.
,
где с=const.
3. ,
т.е. дивергенция суммы 2-х векторных
ф-ций равна сумме дивергенции слангаемых.
,
т.е. дивергенция суммы 2-х векторных
ф-ций равна сумме дивергенции слангаемых.
4.если
U
– скал. ф-ция,
- вектор, то
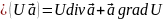 .
.
 (1).
Дивергенцией векторного поля в
точке М наз-ся предел отношения потока
поля через (замкнутую) пов-ть S,
окружающую точку М, к объему тела,
ограниченного этой пов-тью, при условии,
что вся пов-ть стягивается в точку М
(
(1).
Дивергенцией векторного поля в
точке М наз-ся предел отношения потока
поля через (замкнутую) пов-ть S,
окружающую точку М, к объему тела,
ограниченного этой пов-тью, при условии,
что вся пов-ть стягивается в точку М
(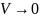 ).
Это определение эквивав.
.
Исходя из физ. смысла потока, можно
сказать, что
).
Это определение эквивав.
.
Исходя из физ. смысла потока, можно
сказать, что
 точка М представ-т собой источник,
откуда жидкость вытекает; при
точка М представ-т собой источник,
откуда жидкость вытекает; при
 точка М есть сток, поглощающий жидкость.
Как следует из (1)
точка М есть сток, поглощающий жидкость.
Как следует из (1)
 хар-ет мощность источника или стока в
т.М. Это и есть физ. смысл дивергенции.
Ясно, что если в объеме V,
ограниченном замкн. пов-тью S,
нет ни источников, ни стоков, то
хар-ет мощность источника или стока в
т.М. Это и есть физ. смысл дивергенции.
Ясно, что если в объеме V,
ограниченном замкн. пов-тью S,
нет ни источников, ни стоков, то
 Векторное
поле,
в кажд. т. кот. див. поля =0,
Векторное
поле,
в кажд. т. кот. див. поля =0, ,
наз-ся соленоидальным
(трубчатым).
,
наз-ся соленоидальным
(трубчатым).
Пример:
найти див. поля лин. скоростей v
жидкости, вращ-ся как ТВ. тело вокруг
неподв. оси с пост. углов. скор.
 .
Решение:
примем ось вр. жидк. за ось Oz.
Тогда, как,
.
Решение:
примем ось вр. жидк. за ось Oz.
Тогда, как,
 .
Имеем:
.
Имеем:
 .
Поле
.
Поле
 - соленоидальное.
- соленоидальное.
