
- •1). Первообразная и неопределённый интеграл. Таблица основных неопределённых интегралов.
- •2).Замена переменной и интегрирование по частям под знаком неопределённого интеграла.
- •6). Интегралы вида: , .
- •7). Интегралы вида: .
- •10). Понятие определённого интеграла, основные свойства определённого интеграла, его вычисление.
- •11.Вычисление площадей плоских фигур, объёмов тел и длин дуг с помощью определённого интеграла.
- •11’.Интегрирование по частям и замена переменной под знаком определённого интеграла.
- •12. Несобственные интегралы 1-го рода.
- •13. Несобственные интегралы 2-го рода.
- •14. Понятие функции нескольких переменных. Предел в точке, непрерывность.
- •15. Частные производные функции двух аргументов, их геометрический смысл.
- •16. Полный дифференциал функции двух и трёх переменных.
- •17. Производные сложной функции нескольких аргументов.
- •19. Дифференцирование неявных функций.
- •20. Частные производные высших порядков.
- •21. Локальный экстремум функции двух аргументов.
- •22. Условный экстремум. Метод множителей Лагранжа.
- •23. Наименьшее и наибольшее значения функции двух аргументов в замкнутой области.
- •24. Двойной интеграл в декартовых координатах. Определение, основные свойства.
- •25. Вычисление двойного интеграла в дск.
- •26. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •27. Вычисление площадей и объёмов с помощью двойного интеграла.
- •28. Тройной интеграл. Определение, основные свойства. Его вычисление в декартовых координатах.
- •29. Цилиндрические координаты. Тройной интеграл в цилиндрических координатах.
- •30. Сферические координаты. Тройной интеграл в сферических координатах.
- •31. Криволинейный интеграл 1-го рода, его свойства и вычисление.
- •32. Криволинейный интеграл 2-го рода, его определение, свойства и вычисление.
- •33. Криволинейный интеграл 2-го рода как работа переменной силы на криволинейном пути.
- •34. Вычисление площади плоской фигуры с помощью кри-2.
- •35. Формула Грина.
- •36. Независимость криволинейного интеграла от пути интегрирования. Нахождение функции по её полному дифференциалу.
- •37. Поверхностный интеграл 1-го рода, его свойства и вычисление. Поверхностный интеграл 2-го рода.
- •38. Вычисление массы поверхности.
- •39. Скалярное поле, производная по направлению.
- •40. Градиент.
- •41. Векторное поле. Дивергенция.
- •42. Поток векторного поля.
- •43. Формула Остроградского.
- •44. Формула Стокса.
- •45. Оператор Гамильтона.
- •46. Оператор Лапласа.
- •47. Потенциальное векторное поле и его свойства.
- •48. Соленоидальное векторное поле.
- •49. Гармоническое векторное поле.
36. Независимость криволинейного интеграла от пути интегрирования. Нахождение функции по её полному дифференциалу.
Пусть
 и
и
 - 2-е произв. точки односвязной области
D
плоскости Oxy
(область D
наз-ся односвязной,
если для люб. замкн. контура, лежащего
в этой обл., ограниченная им часть
плоскости целиком принадлежит D
(области без «дыр»)). Точки А и В можно
соединить различными линиями. По кажд.
их этих кривых интеграл:
- 2-е произв. точки односвязной области
D
плоскости Oxy
(область D
наз-ся односвязной,
если для люб. замкн. контура, лежащего
в этой обл., ограниченная им часть
плоскости целиком принадлежит D
(области без «дыр»)). Точки А и В можно
соединить различными линиями. По кажд.
их этих кривых интеграл:
 имеет, вообще говоря, свое значение.
Если же его знаения по всевозможным
кривым АВ одинаковы, то говорят, что
интеграл I
не зависит от вида пути интегрирования.
в этом случае для инт-ла I
достаточно отметить лишь его нач. точку
А(
имеет, вообще говоря, свое значение.
Если же его знаения по всевозможным
кривым АВ одинаковы, то говорят, что
интеграл I
не зависит от вида пути интегрирования.
в этом случае для инт-ла I
достаточно отметить лишь его нач. точку
А( )
и его конечную точку
пути. Записывают:
)
и его конечную точку
пути. Записывают:
 .
.
Теорема:
для того чтобы КРИ
 не зависел от пути инт-ния в односвязной
обл. D,
в кот. ф-ции P(x,y),
Q(x,y)
непрерывны вместе со своими частными
производными, необходимо и достаточно,
чтобы в кажд. точке этой обл. выполнялось
условие
не зависел от пути инт-ния в односвязной
обл. D,
в кот. ф-ции P(x,y),
Q(x,y)
непрерывны вместе со своими частными
производными, необходимо и достаточно,
чтобы в кажд. точке этой обл. выполнялось
условие
 .
.
Если
это условие выполняется, то подынтегральное
выражение P(x,y)dx+Q(x,y)dy
явл. полным дифференциалом нек. ф-ции
u=u(x,y),
т.е. P(x,y)dx+Q(x,y)dy=dU(x,y).
Тогда:
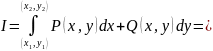
 ,
т.е.
,
т.е.
 (1).
(1).
Ф-ла (1) – обобщенная ф-ла Ньютона-Лейбница для КРИ от полного дифференциала.
Теорема:
если
подынтегральное выр. Pdx+Qdy
есть полный дифференциал и путь
интегрирования L
замкнутый, то
 .
.
Замечания:1.чтобы не спутаь переем. интег-ния х с верхним пределом х, переменную интегр-ния обозначают другой буквой.
2.ф-цию
U=U(x,y),
удовлетворяющую условию
,
можно найти, исп-зуя ф-лу:
 .
В кач. нач. точки (
)
обычно берут (0,0).
.
В кач. нач. точки (
)
обычно берут (0,0).
3.аналогичные
рез-ты справедливы для КРИ:
 по пространственной кривой. Соответственно:
по пространственной кривой. Соответственно:
 ,
,
 ,
,
 .
.
37. Поверхностный интеграл 1-го рода, его свойства и вычисление. Поверхностный интеграл 2-го рода.
 Обобощние
2-го инит-ла явл. поверхностный инт-л
(ПИ).
Обобощние
2-го инит-ла явл. поверхностный инт-л
(ПИ).
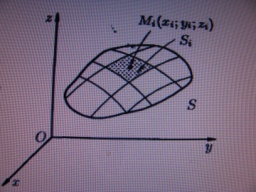
Пусть
в точках нек. поверхности S,
с площ. S,
пространства Oxyz
определена непрер. ф-ция f(x,y,z).
Разобьем пов-ть S
на n
частей
 ,
площади которых обозначим через
,
а диаметры – через
.
В кажд. части
возьмем проив. точку
и составим сумму
,
площади которых обозначим через
,
а диаметры – через
.
В кажд. части
возьмем проив. точку
и составим сумму
 .
Она наз-ся интегральной
суммой
для ф-ции f(x,y,z)
по
поверхности S.
Если инт-ная сумма имеет предел, то он
наз-ся поверхностным
интегралом 1-го рода ПИ-1
от ф-ции f(x,y,z)
по поверхности S
и обозначается
.
Она наз-ся интегральной
суммой
для ф-ции f(x,y,z)
по
поверхности S.
Если инт-ная сумма имеет предел, то он
наз-ся поверхностным
интегралом 1-го рода ПИ-1
от ф-ции f(x,y,z)
по поверхности S
и обозначается
 .
Таким образом:
.
Таким образом:
 .
.
Если поверхность S гладкая (в каждой ее точке существует касательная плоскость, кот. непрерывно меняется с перемещением точки по поверхности), а ф-ция f(x,y,z) непрерывна на этой пов-ти, то ПИ существует.
Св-ва
ПИ-1:1. .
.
2. .
.
3.если
пов-ть S
разбить на части
 и
и
 такие, что
такие, что
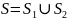 ,
а пересечение
и
состояит лишь из границы, их разделяющей,
то
,
а пересечение
и
состояит лишь из границы, их разделяющей,
то
 .
.
4.если
на поверхности S
выполнено нер-во
 ,
то
,
то
 .
.
5. ,
S
– площадь поверхности S.
,
S
– площадь поверхности S.
6. .
.
7.если
f(x,y,z)
непрерывна на поверхности S,
то на этой пов-ти сущ-ет точка
 такая, что:
такая, что:
 .
(теорема о среднем значении).
.
(теорема о среднем значении).
Вычисление ПИ-1:
Ф-ла
выражающая инт-л по пов-ти S
через 2-ной инт-л по проекции S
на плоскость Oxy:
 .
.
Если
пов-ть S
задана ур. вида
 ,
то аналогично получим:
,
то аналогично получим: и
и
 .
Где
.
Где
 - поекции пов-ти S
на корд. плоскости Oxz
и Oyz
соответственно.
- поекции пов-ти S
на корд. плоскости Oxz
и Oyz
соответственно.

![]()

Поверхностный интеграл 2-го рода.
![]() Пусть
задана двусторонняя
поверхностьи (таковой
явл. плоскость, эллипсоид, любая пов-ть,
задаваемая ур.z=f(x,y),
где f(x,y),
Пусть
задана двусторонняя
поверхностьи (таковой
явл. плоскость, эллипсоид, любая пов-ть,
задаваемая ур.z=f(x,y),
где f(x,y),
 и
и
 - ф-ции, непрерывные в нек. обл. D
плоскости Oxy
и т.д.).
После
обхода такой пов-ти, не пересекая ее
гр., направление нормали к ней не
меняется. Пример односторонней
пов-ти:
лист
Мебиуса,
получающийся при склеивании сторон АВ
и CD
прямоугольника ABCD
так, что т.А совмещается с точкой С, а В
– c
D.
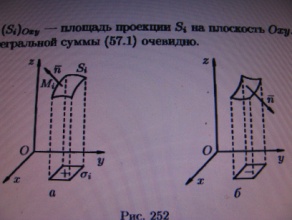
Далее, пусть в точках рассматриваемой
2-сторонней пов-ти S
в пространстве Oxyz
определена непрерывная ф-ция f(x,y,z).
Выбранную сторону пов-ти (в таком случае
говорят, что поверхность ориентированна)
разбита на части
и проектируем их на коорд. плоскости.
При этом площ. проекции
- ф-ции, непрерывные в нек. обл. D
плоскости Oxy
и т.д.).
После
обхода такой пов-ти, не пересекая ее
гр., направление нормали к ней не
меняется. Пример односторонней
пов-ти:
лист
Мебиуса,
получающийся при склеивании сторон АВ
и CD
прямоугольника ABCD
так, что т.А совмещается с точкой С, а В
– c
D.
Далее, пусть в точках рассматриваемой
2-сторонней пов-ти S
в пространстве Oxyz
определена непрерывная ф-ция f(x,y,z).
Выбранную сторону пов-ти (в таком случае
говорят, что поверхность ориентированна)
разбита на части
и проектируем их на коорд. плоскости.
При этом площ. проекции
 берем со знаком +, если выбрана верхняя
стор. пов-ти, или, что то же самое, если
нормаль
берем со знаком +, если выбрана верхняя
стор. пов-ти, или, что то же самое, если
нормаль
 к выбранной стороне пов-ти составляет
с осью Oz
острый угол, т.е.
к выбранной стороне пов-ти составляет
с осью Oz
острый угол, т.е.
 ;
со знаком -, если выбрана нижняя стор.
пов-ти (или
;
со знаком -, если выбрана нижняя стор.
пов-ти (или
 ).
В этом случае интегр-я сумма:
).
В этом случае интегр-я сумма:
 ,
где
,
где
 - площ. проекции
на плоск. Oxy.
Ее отличие от инт-ной суммы очевидно.
- площ. проекции
на плоск. Oxy.
Ее отличие от инт-ной суммы очевидно.
 Если
предел инт-ной суммы существует и не
зависит от способа разбиения пов-ти S
на части
и от выбора точек
Если
предел инт-ной суммы существует и не
зависит от способа разбиения пов-ти S
на части
и от выбора точек
 наз-ся ПИ-2
от ф-ции f(x,y,z)
по переменным x,
y
по выбранной стороне поверхности и
обозначается:
наз-ся ПИ-2
от ф-ции f(x,y,z)
по переменным x,
y
по выбранной стороне поверхности и
обозначается:
 .
Итак:
.
Итак:
 .
Аналогично определяются ПИ-2 по пер.
y,z
и z,x:
.
Аналогично определяются ПИ-2 по пер.
y,z
и z,x:
 ,
,
 .
.
Общим
видом ПИ-2 служит инт-л:
 ,
где P,Q,R
– непрерывные ф-ции, определенные в
точках 2-стогр. пов. S.
,
где P,Q,R
– непрерывные ф-ции, определенные в
точках 2-стогр. пов. S.
Отметим,
что S
– замкнутая пов-ть, то ПИ по внешней
стороне ее обозначается
 ,
по внутренней
,
по внутренней
 .
.

 Св-ва
ПИ-2:1.ПИ-2
изме-т знак при перемене стороны пов-ти.
2.постоянный
множитель можно выносить за знак ПИ.3.ПИ
от суммы ф-ций равен сумме соответствующих
инт-ов от слагаемых4.ПИ-2
по всей пов-ти
Св-ва
ПИ-2:1.ПИ-2
изме-т знак при перемене стороны пов-ти.
2.постоянный
множитель можно выносить за знак ПИ.3.ПИ
от суммы ф-ций равен сумме соответствующих
инт-ов от слагаемых4.ПИ-2
по всей пов-ти
 (аддитивное
св-во), если
и
пересекаются лишь по гр., их
разделяющей.5.если
(аддитивное
св-во), если
и
пересекаются лишь по гр., их
разделяющей.5.если
 - цилиндрич. пов-ти с образующими, ||
соответственно осям Oz,Ox,Oy,
то:
- цилиндрич. пов-ти с образующими, ||
соответственно осям Oz,Ox,Oy,
то:
 .
.
![]()
![]() Вычисление
ПИ-2: Выберем
ту сторону по-ти S,
где нормаль к ней образует с осью Oz
острый угол. Т.к.
Вычисление
ПИ-2: Выберем
ту сторону по-ти S,
где нормаль к ней образует с осью Oz
острый угол. Т.к.
 ,
то интегр. сумма может быть записана в
виде:
,
то интегр. сумма может быть записана в
виде:
 .
Правая часть эт. рав-ва есть инт-ная
сумма для ф-ции R(x,y,z(x,y)),
непрерывной в обл. D.
Переходя к пределу , получаем:
.
Правая часть эт. рав-ва есть инт-ная
сумма для ф-ции R(x,y,z(x,y)),
непрерывной в обл. D.
Переходя к пределу , получаем:
 ,
выражащую ПИ-2 по переменным x,y
через 2-ной инт-л. Если выбрать сторону,
т.е. нижнюю, пов-ти S,
то полученный 2-ной инт-л берут со зн.
-. Поэтому:
,
выражащую ПИ-2 по переменным x,y
через 2-ной инт-л. Если выбрать сторону,
т.е. нижнюю, пов-ти S,
то полученный 2-ной инт-л берут со зн.
-. Поэтому:
 ,
аналогично:
,
аналогично:
 ,
,
 .
.
 ,
,
 - проекции пов-ти S
на плоскости Oxz
и Oyz
соотв-но (замкнутые). Знаки перед инт-ом
выбираются в зависимости от ориентации
пов-ти S:
+ еслинормаль к пов-ти образует с осью
Oy
острый угол, - если тупой. Для вычисления
общ. ПИ-2 исп-ют эти 3 ф-лы, проектируя
пов-ть S
на все три корд. плоск-ти:
- проекции пов-ти S
на плоскости Oxz
и Oyz
соотв-но (замкнутые). Знаки перед инт-ом
выбираются в зависимости от ориентации
пов-ти S:
+ еслинормаль к пов-ти образует с осью
Oy
острый угол, - если тупой. Для вычисления
общ. ПИ-2 исп-ют эти 3 ф-лы, проектируя
пов-ть S
на все три корд. плоск-ти:
 .
.
 .
.
Замечание:
 ,
ds-эл-т
площади пов-ти S;
,
ds-эл-т
площади пов-ти S;
 – направляющие косинусы нормали
к выбранной стороне пов-ти S.
ПИ-1 и ПИ-2 связаны:
– направляющие косинусы нормали
к выбранной стороне пов-ти S.
ПИ-1 и ПИ-2 связаны:
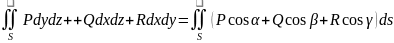 .
.
