Задание 12
1) Постройте аналогичную модель для сетевого графика, приведенного на листе з12 Вашего рабочего файла.
2) Убедитесь в правильности ее функционирования, задавая различные варианты исходных данных. Основные результаты рекомендуется нанести непосредственно на график.
11. Вычисление обратной матрицы
Известно, что при расчете межотраслевого баланса потребуется, как и в ряде других расчетов, вычислять обратную матрицу. В Excel есть функция МОБР, единственным аргументом которой является блок ячеек, содержащих исходную матрицу. В приведенном примере такому блоку присвоено имя Исходная_матрица. Но эта функция возвращает результат в виде массива, размещенного в одной ячейке. Поэтому, чтобы сформировать обратную матрицу, необходимо использовать один из приведенных ниже способов.
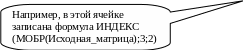
Первый способ основан на использовании функции ИНДЕКС, которая в списке функций находится в категории Ссылки и массивы.
В качестве аргументов этой функции надо указать функцию МОБР вместе с ее аргументом, а также индексы строки и столбца. Пример выполнения таких вычислений приведен ниже (рис. 11.1). Можно рекомендовать следующий порядок ввода этих формул. Сначала вызвать функцию ИНДЕКС, выбирая первый из возможных списков аргументов (первым аргументом в этом списке будет массив). При запросе на ввод массива щелкните по любой пустой ячейке, а в поля для номеров строки и столбца введите по единице. В результате получится ноль, но достаточно в записанном выражении выделить временно введенную пустую ячейку и вызвать функцию МОБР, указав в качестве ее аргумента исходную матрицу, чтобы получить элемент обратной матрицы с заданными индексами. Копируем эту ячейку в остальные ячейки столбца, исправляем индексы, затем заполняем остальные элементы матрицы.
Для матрицы большей размерности такое исправление индексов становится трудоемким и можно применить второй вариант выполнения вычислений. Если ввести в соответствующие ячейки величины индексов для строк и столбцов, то в выражении для элемента a*11 обратной матрицы на позиции для индексов надо указать ссылки на ячейки с единичными значениями индексов. Сделаем абсолютными адрес столбца для ячейки с индексом строки и адрес строки для ячейки с индексом столбца. Тогда при копировании вычисленного элемента получим все элементы обратной матрицы без редактирования индексов.
Чтобы убедиться в правильности вычислений, присвоим ячейкам с полученным результатом имя Обратная_матрица и перемножим эти матрицы, используя функцию МУМНОЖ (рис. 11.1). Должна получиться единичная матрица. Так как все вычисления реализуются с ограниченной точностью, то возможно появление вместо нулей малых по абсолютной величине значений.
Исходная матрица Обратная матрица
Индексы 1 2 3
1
1
2 3 -2,167 0,8333 0,3333
2 3 4 5 1,8333 -0,167 -0,667
3 2 3 7 -0,167 -0,167 0,3333
Единичная матрица
1 0 0 -2,167 0,8333 0,3333
0 1 0 1,8333 -0,167 -0,667
0 0 1 -0,167 -0,167 0,3333
Рис. 11.1. Вычисление обратной матрицы
Второй способ основан на использовании формулы массива, которая может выполнить требуемые вычисления, а затем вернуть всю группу значений. Для этого необходимо предварительно выделить диапазон ячеек, которые будут содержать результаты вычислений, потом ввести формулу, но вместо того, чтобы нажимать клавишу ENTER или щелкать по кнопке OK в диалоговом окне мастера функций, следует нажать клавиши CTRL+SHIFT+ENTER.
При вводе формулы массива Microsoft Excel автоматически заключает ее в фигурные скобки ({ }). Для рассматриваемой задачи вычисления обратной матрицы в каждой ячейке выделенного диапазона будет одна и та же формула {=МОБР(B44:D46)}. В этом случае для ссылки на ячейки, содержащие исходную матрицу, нельзя использовать ни имя этой группы, ни абсолютную адресацию.
Использование формулы массива позволяет быстрее ввести необходимые формулы, однако запись становится менее наглядной, поэтому ниже используется функция ИНДЕКС.