Вопросы и задачи к лекции 12

141-1. Дайте определение магнитного момента системы токов.

142-2. Равномерно заряженный шар вращается с постоянной угловой скоростью ω вокруг оси проходящей через центр шара. Найдите магнитный момент, если плотность заряда ρ, а радиус шара R.

143-3. Получите выражение для магнитного момента тока, протекающего по витку бесконечно малого сечения, расположенному в плоскости.

144-4. Найдите магнитный момент тока, протекающего по прямоугольному контуру, изогнутому под прямым углом (рис. 2.76).

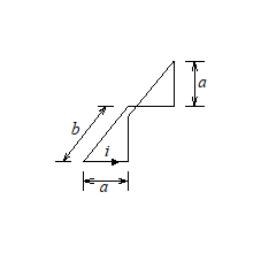
Рис. 2.76. Прямоугольный контур, изогнутый под прямым углом

145-5. Запишите выражение для векторного потенциала системы замкнутых токов на далеких расстояниях от системы.

146-6. Запишите выражение для индукции магнитного поля системы замкунутых токов на далеких расстояниях от системы.

147-7. Докажите, что магнитный момент системы замкнутых токов не зависит от выбора начала системы координат.

148-8. Ток протекает по круговому витку радиуса (рис. 2.77). Найдите точное значение индукции магнитного поля на оси в точке М и приближенное значение (используя магнитный момент), если . Сравните эти значения.

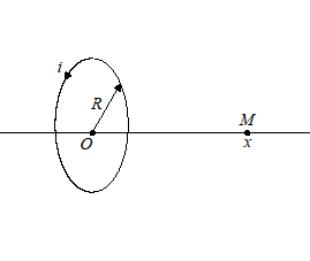
Рис. 2.77. Круговой виток с током

Вопросы и задачи к лекции 13

149-1. Источники электромагнитного поля и равны нулю во всех точках пространства и в любой момент времени t ( ). Возможно ли существование такого магнитного поля в указанные моменты времени t?

150-2. Источники электромагнитного поля и равны нулю во всех точках пространства и в любой момент времени t ( ). Возможно ли существование такого электрического поля в указанные моменты времени t?

151-3. Какому уравнению удовлетворяет поле при отсутствии источников и в данной части пространства в любой момент времени? Выведите это уравнение.

152-4. Какому уравнению удовлетворяет поле при отсутствии источников и в данной части пространства в любой момент времени? Выведите это уравнение.

153-5. Покажите, что плоская электромагнитная волна является поперечной по отношению к фронтовой нормали , т.е. и .

154-6. В фиксированный момент времени и в фиксированной точке вектор падающей плоской волны имеет значение . Найдите вектор в этот же момент времени и в этой же точке.

155-7. Вектор отраженной плоской волны в точке М в момент времени t имеет направление, указанное на рис. 2.81, т.е. . Найдите направления векторов и в той же точке и в тот же момент времени.

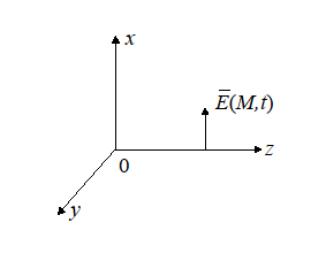
Рис. 2.81. К определению направлений векторов и по заданному направлению отраженной плоской волны

156-8. Докажите, что скорость переноса энергии в отраженной плоской волне равна .

Вопросы и задачи к лекции 14

157-1. Комплексная амплитуда индукции магнитного поля плоской падающей волны имеет выражение:

.

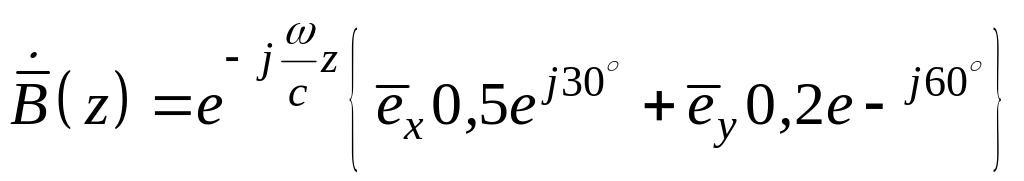Какой поляризации эта волна?

158-2. Проекции магнитного поля плоской монохроматической волны имеют выражения:

,

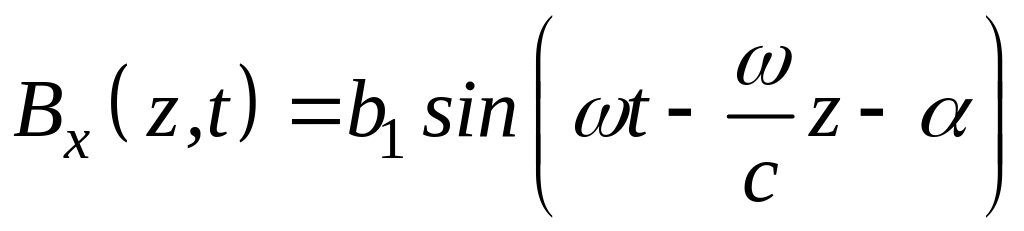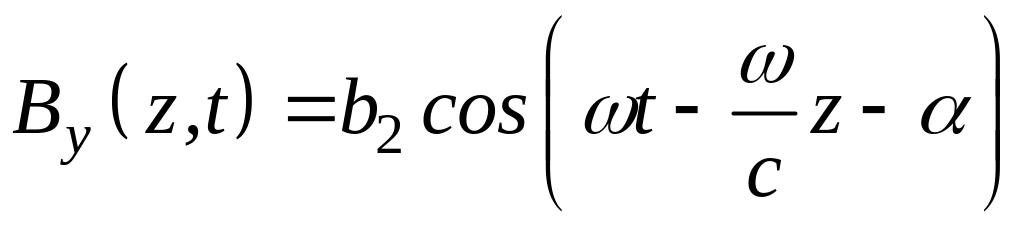. ; . Какой поляризации эта волна? При некоторых и . Найдите .

159-3. Проекции магнитного поля плоской монохроматической волны имеют выражения:

,

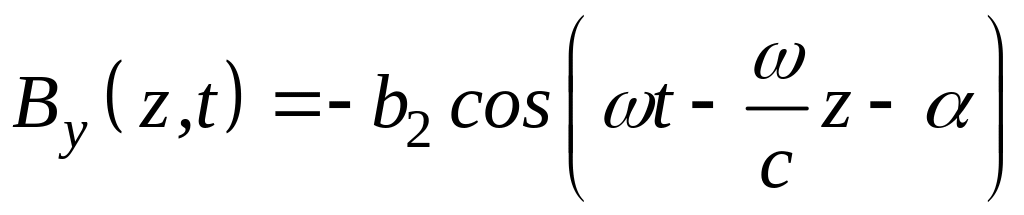, причем . Какой поляризации эта волна?

160-4. Проекции электрического поля плоской монохроматической волны имеют выражения:

,

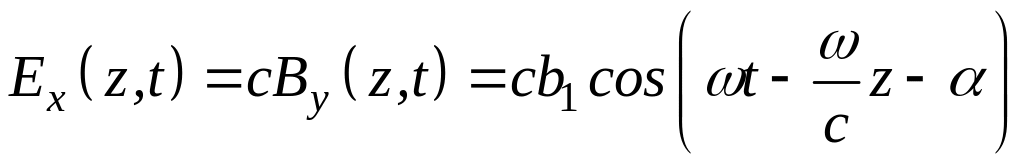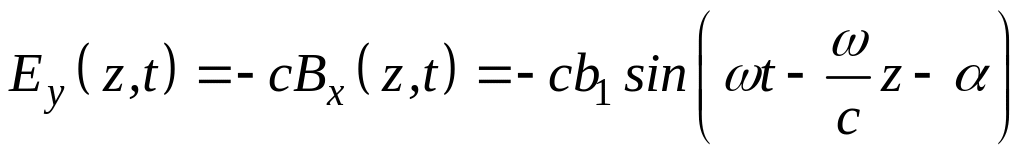. Какой поляризации эта волна?

161-5. х-овая компонента поля плоской монохроматической волны имеет выражение . Запишите выражения для , и , если известно, что данная волна левой круговой поляризации.

162-6. Запишите выражения для , , и для линейно поляризованной вдоль оси волны.

163-7.Докажите, что линейно поляризованная волна представляет собой суперпозицию двух волн круговой поляризации.

164-8. Докажите, что эллиптически поляризованная волна представляет собой суперпозицию двух волн линейной поляризации.