
- •Вопросы и задачи к лекции 2
- •Вопросы и задачи к лекции 4
- •Вопросы и задачи к лекции 5
- •Вопросы и задачи к лекции 6
- •Вопросы и задачи к лекции 7
- •Вопросы и задачи к лекции 8
- •Вопросы и задачи к лекции 9
- •Вопросы и задачи к лекции 10
- •Вопросы и задачи к лекции 11
- •Вопросы и задачи к лекции 12
- •Вопросы и задачи к лекции 13
- •Вопросы и задачи к лекции 14
- •Вопросы и задачи к лекции 15
- •Вопросы и задачи к лекции 20
- •Вопросы и задачи к лекции 21
- •Вопросы и задачи к лекции 22
- •Вопросы и задачи к лекции 23
- •Вопросы и задачи к лекции 24
- •Вопросы и задачи к лекции 25
- •Вопросы и задачи к лекции 28
- •Вопросы и задачи к лекции 29
- •Вопросы и задачи к лекции 30
- •Вопросы и задачи к лекции 31
Вопросы и задачи к лекции 7
93-1. Дайте определение векторного потенциала электромагнитного поля
94-2.
Магнитное поле
изменяется по закону
![]() (рис. 2.45). Найдите какой-либо векторный
потенциал этого поля
(рис. 2.45). Найдите какой-либо векторный
потенциал этого поля
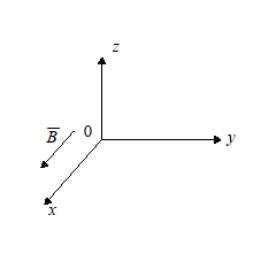
Рис. 2.45. Пример определения векторного потенциала по заданной индукции магнитного поля
95-3. Дайте определение скалярного потенциала электромагнитного поля.
96-4. Что называют калибровочными градиент-преобразованиями электродинамических потенциалов? Какие величины электромагнитного поля они не изменяют?
97-5. Сформулируйте условие калибровки Лоренца.
98-6. Запишите дифференциальные уравнения для электродинамических потенциалов, которые получаются при использовании калибровки Лоренца.
99-7. Что такое укороченные калибровочные градиент-преобразования?
100-8. Сформулируйте условия калибровки Кулона.
101-9. Однородный проводящий шар находится в однородном переменном во времени магнитном поле. Какую калибровку целесообразно применить при решении этой задачи с помощью электродинамических потенциалов?
Вопросы и задачи к лекции 8
102-1.
Запишите дифференциальные уравнения
для электродинамических потенциалов
внутри и вне объема
![]() ,
если движущиеся заряды имеются в объеме
и отсутствуют вне объема
.
,
если движущиеся заряды имеются в объеме
и отсутствуют вне объема
.
103-2. В чем смысл решения волнового уравнения методом Даламбера?
104-3. Запишите формулу для запаздывающего скалярного потенциала.
105-4. Запишите формулу для запаздывающего векторного потенциала.
106-5.
Запишите формулы для электродинамических
потенциалов в случае, когда заряды в
объеме
неподвижны и не изменяются во времени
(![]() ,
,
![]() ).
).
107-6.
Запишите формулы для электродинамических
потенциалов в случае, когда плотность
тока
и плотность заряда
не зависят от времени (![]() ,
,
![]() ).
В какой физической ситуации это возможно?
).
В какой физической ситуации это возможно?
108-7.
На рис. 2.47 изображен объем
![]() и две точки наблюдения
и две точки наблюдения
![]() и
и
![]() .
Известно, что
.
Известно, что
![]() .
.
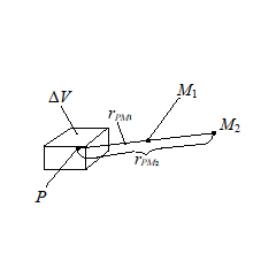
Рис. 2.47. Объем с изменяющимся зарядом
В
момент времени
![]() заряд в объеме
равен
заряд в объеме
равен
![]() , а в момент времени
, а в момент времени
![]() заряд в объеме
равен
заряд в объеме
равен
![]() .
Как выражается заряд
через заряд
,
если скалярный потенциал зарядов объема
в точке М1
в момент времени
.
Как выражается заряд
через заряд
,
если скалярный потенциал зарядов объема
в точке М1
в момент времени
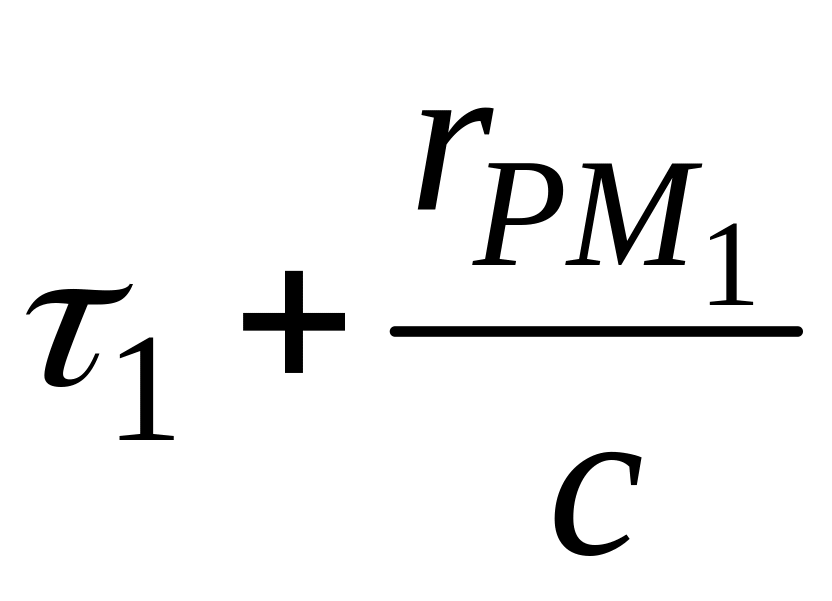 равен потенциалу зарядов объема
в точке М2
в момент времени
равен потенциалу зарядов объема
в точке М2
в момент времени
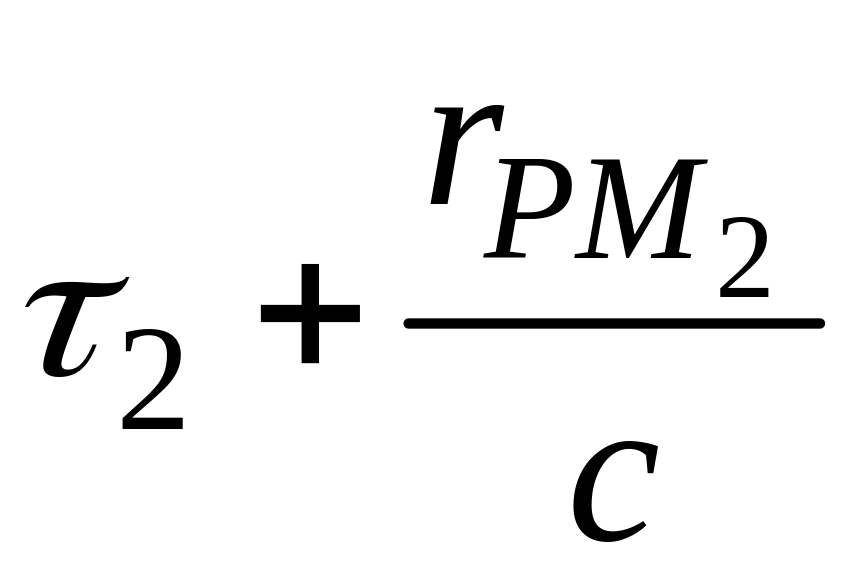 ?
?
Вопросы и задачи к лекции 9
109-1.
Выведите выражение для скалярного
потенциала произвольно движущегося
точечного заряда. Каким будет это
выражение при
и при
![]() ?
?
110-2. Выведите выражение для векторного потенциала произвольно движущегося точечного заряда. Каким будет это выражение при и при ?
111-3. Запишите выражение, связывающее векторный и скалярный потенциалы произвольно движущегося точечного заряда.
112-4.
Используя формулы для потенциалов
Лиенара-Вихерта, найдите скалярный и
векторный потенциалы в центре окружности,
по которой движется точечный заряд
с постоянной угловой скоростью
![]() (рис. 2.55). Радиус окружности
.
В момент времени
(рис. 2.55). Радиус окружности
.
В момент времени
![]() заряд находился в точке
заряд находился в точке
![]() .
.
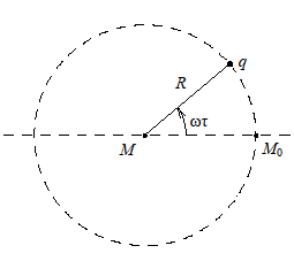
Рис. 2.55. К определению потенциалов Лиенара-Вихерта точечного заряда равномерно движущегося по окружности
113-5.
Точечный
заряд движется равномерно и прямолинейно
вдоль оси х
(рис. 2.56).
Используя потенциалы Лиенара-Вихерта,
найдите скалярный и векторный потенциалы
в точке
в момент времени
![]() .
.
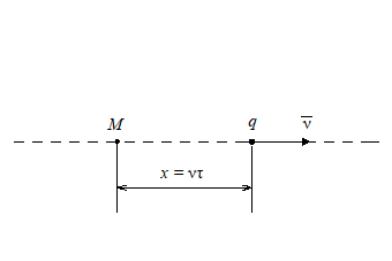
Рис. 2.56. К определению потенциалов Лиенара-Вихерта равномерно движущегося точечного заряда
114-6.
Докажите эквивалентность двух определений
электростатического потенциала
![]() ,
,
![]() и
и
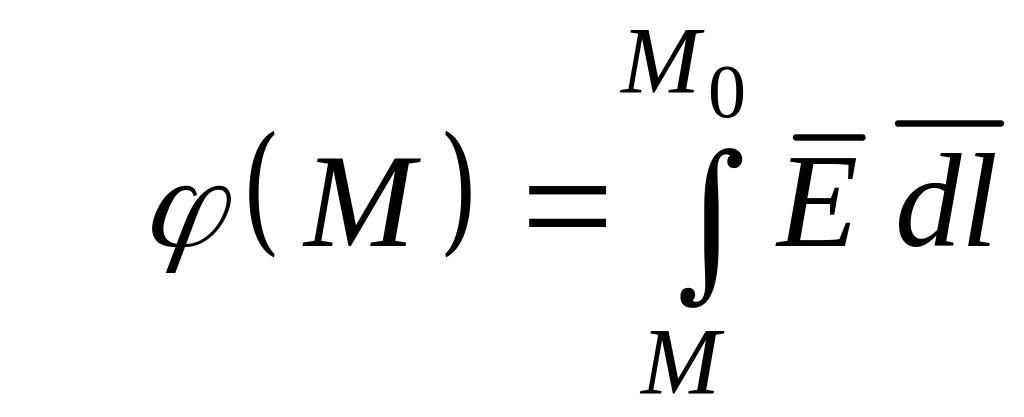 .
.
115-7. Выведите из формулы для запаздывающего скалярного потенциала формулу для электростатического объемного потенциала.
116-8.
В объеме V
распределены заряды с плотностью
![]() .
Вне V
заряды отсутствуют (рис. 2.57). Запишите
дифференциальные уравнения для
электростатического потенциала внутри
и вне объема V.
.
Вне V
заряды отсутствуют (рис. 2.57). Запишите
дифференциальные уравнения для
электростатического потенциала внутри
и вне объема V.
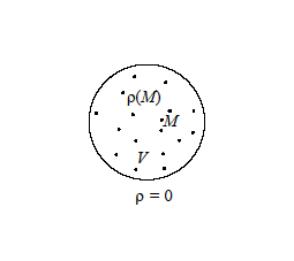
Рис. 2.57. К записи дифференциальных уравнений для электростатического потенциала в различных областях
117-9. Используя выражение для напряженности электрического поля точечного заряда и принцип суперпозиции, получите выражение для напряженности электрического поля зарядов, находящихся в объеме V (см задачу 116-8).
118-10.
Стержень длиной 2а
равномерно заряжен (рис. 2.58). Заряд на
единицу длины равен τ.
Найдите напряженность электрического
поля в точках
и
.
К каким значениям будут стремиться эти
напряженности при
![]() .
В случае
.
В случае
![]() найдите напряженности в точках
и
с помощью теоремы Гаусса в интегральной
форме. Сравните эти значения с предельными.
найдите напряженности в точках
и
с помощью теоремы Гаусса в интегральной
форме. Сравните эти значения с предельными.
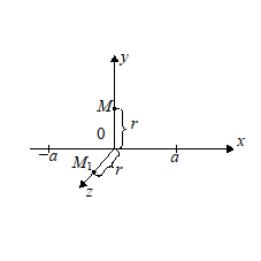
Рис. 2.58. Равномерно заряженный стержень конечной длины
