
- •Вопросы и задачи к лекции 2
- •Вопросы и задачи к лекции 4
- •Вопросы и задачи к лекции 5
- •Вопросы и задачи к лекции 6
- •Вопросы и задачи к лекции 7
- •Вопросы и задачи к лекции 8
- •Вопросы и задачи к лекции 9
- •Вопросы и задачи к лекции 10
- •Вопросы и задачи к лекции 11
- •Вопросы и задачи к лекции 12
- •Вопросы и задачи к лекции 13
- •Вопросы и задачи к лекции 14
- •Вопросы и задачи к лекции 15
- •Вопросы и задачи к лекции 20
- •Вопросы и задачи к лекции 21
- •Вопросы и задачи к лекции 22
- •Вопросы и задачи к лекции 23
- •Вопросы и задачи к лекции 24
- •Вопросы и задачи к лекции 25
- •Вопросы и задачи к лекции 28
- •Вопросы и задачи к лекции 29
- •Вопросы и задачи к лекции 30
- •Вопросы и задачи к лекции 31
Вопросы и задачи к лекции 5
69-1. Сформулируйте принцип непрерывности магнитного потока в интегральной форме.
70-2. Запишите систему уравнений Максвелла для поля зарядов и токов в вакууме в интегральной форме.
71-3. Выведите принцип непрерывности электрического тока в интегральной форме из закона полного тока в интегральной форме.
72-4. Исходя из закона полного тока в интегральной форме и теоремы Гаусса в интегральной форме, выведите закон сохранения заряда в интегральной форме.
73-5. Пользуясь математическими теоремами Стокса и Гаусса-Остроградского, выведите уравнения Максвелла в дифференциальной форме из уравнений Максвелла в интегральной форме.
74-6. Запишите систему уравнений Максвелла для поля зарядов и токов в вакууме в дифференциальной форме.
75-7. Пользуясь математическими теоремами Стокса и Гаусса-Остроградского, выведите уравнения Максвелла в интегральной форме из уравнений Максвелла в дифференциальной форме.
76-8. Выведите принцип непрерывности электрического тока в дифференциальной форме из системы уравнений Максвелла в дифференциальной форме.
77-9. То же для закона сохранения заряда.
78-10. Исходя из принципа непрерывности магнитного потока, сформулировать первый закон Кирхгофа для узла магнитной цепи (рис. 2.38).
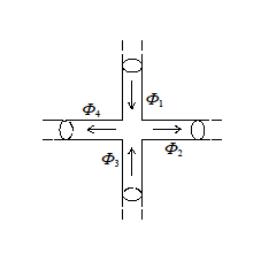
Рис. 2.38. К выводу первого закона Кирхгофа для узла магнитной цепи
Вопросы и задачи к лекции 6
79-1.
Запишите выражения для произведения
![]() через энергию движущихся заряженных
частиц.
через энергию движущихся заряженных
частиц.
80-2. Какой смысл имеет произведение внутри проводника с током (закон Джоуля-Ленца в дифференциальной форме)?
81-3. Запишите выражение для плотности энергии электрического поля и докажите его.
82-4. Запишите выражение для плотности энергии магнитного поля и докажите его.
83-5. Дайте определение вектора Пойнтинга. Какой смысл он имеет?
84-6. Сформулируйте закон сохранения энергии в электродинамике (теорему Умова-Пойнтинга) в интегральной форме.
85-7. Сформулируйте теорему Умова-Пойнтинга в дифференциальной форме.
86-8. Сформулируйте теорему Умова-Пойнтинга в интегральной форме для случая, когда внутри замкнутой поверхности находятся проводники с током (или их части).
87-9. Сформулируйте теорему Умова-Пойнтинга в дифференциальной форме внутри проводника с током.
88-10.
По бесконечно длинному прямолинейному
проводнику кругового сечения радиуса
протекает постоянный ток
![]() (рис. 2.42). Покажите, что поток вектора
Пойнтинга сквозь замкнутую поверхность
цилиндра длиной
и радиуса основания
снаружи вовнутрь равен мощности тепловых
потерь
(рис. 2.42). Покажите, что поток вектора
Пойнтинга сквозь замкнутую поверхность
цилиндра длиной
и радиуса основания
снаружи вовнутрь равен мощности тепловых
потерь
![]() ,
где
– сопротивление части проводника длиной
.
Сквозь какие части замкнутой поверхности
поток энергии равен нулю (боковую
поверхность или основания цилиндра)?
,
где
– сопротивление части проводника длиной
.
Сквозь какие части замкнутой поверхности
поток энергии равен нулю (боковую
поверхность или основания цилиндра)?
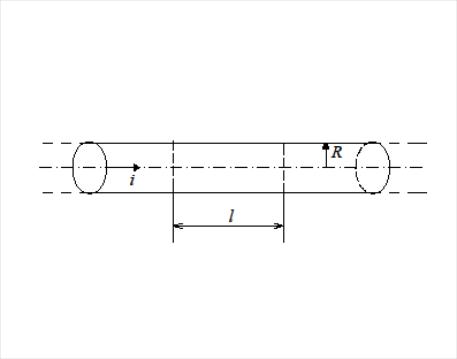
Рис. 2.42. К расчету потока энергии в прямолинейном проводнике, по которому протекает постоянный ток
89-11.
Происходит зарядка конденсатора с
круглыми пластинами радиуса
и бесконечно длинными прямолинейными
проводниками (рис. 2.43). Покажите, что
поток вектора Пойнтинга сквозь замкнутую
цилиндрическую поверхность
снаружи вовнутрь в любой момент времени
равен скорости увеличения электрической
энергии между обкладками конденсатора
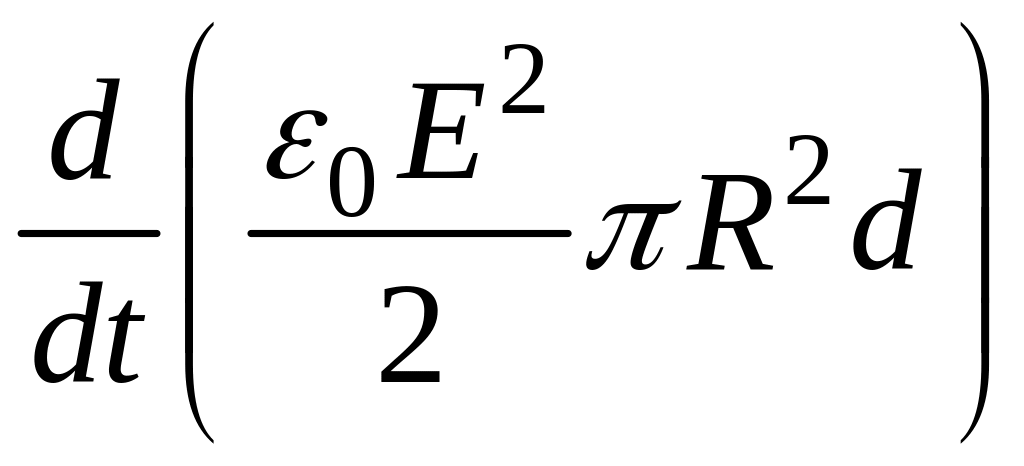 ,
где
,
где
![]() ‑
напряженность электрического поля
между пластинами конденсатора,
– расстояние между обкладками
конденсатора. Считать, что поле
однородное вплоть до боковой поверхности
цилиндра, ограниченного замкнутой
поверхностью
.
Сквозь какие части замкнутой поверхности
поток энергии равен нулю (боковую
поверхность или основания цилиндра)?
‑
напряженность электрического поля
между пластинами конденсатора,
– расстояние между обкладками
конденсатора. Считать, что поле
однородное вплоть до боковой поверхности
цилиндра, ограниченного замкнутой
поверхностью
.
Сквозь какие части замкнутой поверхности
поток энергии равен нулю (боковую
поверхность или основания цилиндра)?
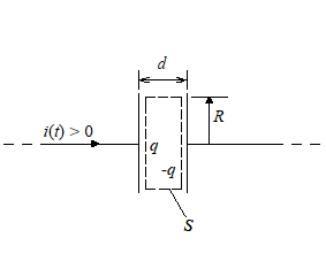
Рис. 2.43. К расчету потока энергии в плоском конденсаторе, по которому протекает переменный ток
90-12.
По соленоиду, сечение которого изображено
на рис. 2.44 протекает положительный ток
![]() ,
возрастающий во времени. Длина соленоида
,
радиус
.
Покажите, что поток вектора Пойнтинга
сквозь замкнутую цилиндрическую
поверхность
снаружи вовнутрь в любой момент времени
равен скорости увеличения энергии
магнитного поля в объеме цилиндра
ограниченного этой поверхностью
,
т.е. равен
,
возрастающий во времени. Длина соленоида
,
радиус
.
Покажите, что поток вектора Пойнтинга
сквозь замкнутую цилиндрическую
поверхность
снаружи вовнутрь в любой момент времени
равен скорости увеличения энергии
магнитного поля в объеме цилиндра
ограниченного этой поверхностью
,
т.е. равен
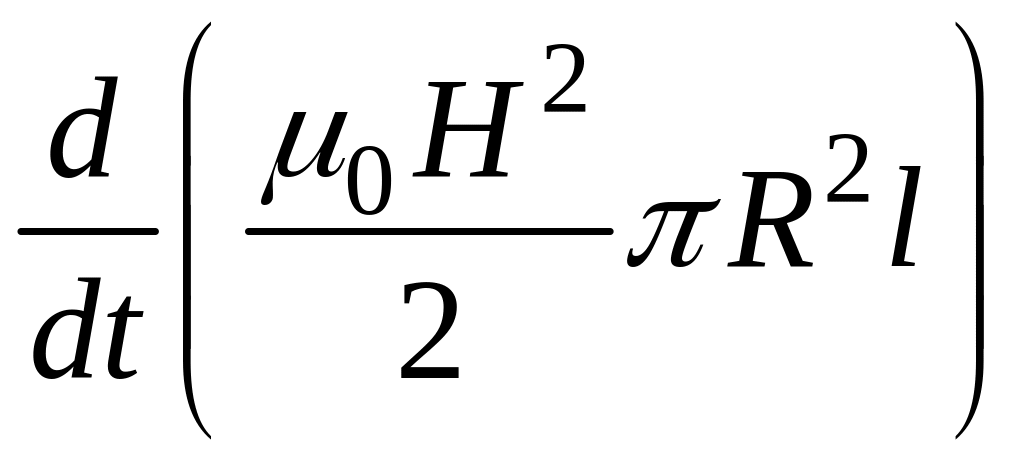 ,
где
,
где
![]() ‑ напряженность магнитного поля
внутри соленоида. Считать что поле
‑ напряженность магнитного поля
внутри соленоида. Считать что поле
![]() внутри соленоида однородное вплоть до
оснований цилиндра, ограниченного
замкнутой поверхностью
.
Сквозь какие части замкнутой поверхности
поток энергии равен нулю (боковую
поверхность или основания цилиндра)?
внутри соленоида однородное вплоть до
оснований цилиндра, ограниченного
замкнутой поверхностью
.
Сквозь какие части замкнутой поверхности
поток энергии равен нулю (боковую
поверхность или основания цилиндра)?
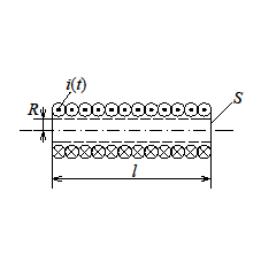
Рис. 2.44. К расчету потока энергии в соленоиде, по которому протекает переменный ток
91-13. Представьте вектор Пойнтинга в гармоническом электромагнитном поле в виде суммы постоянной составляющей и колеблющейся составляющей.
92-14. Что такое комплексный вектор Пойнтинга и каким свойством он обладает?
