
- •Вопросы и задачи к лекции 2
- •Вопросы и задачи к лекции 4
- •Вопросы и задачи к лекции 5
- •Вопросы и задачи к лекции 6
- •Вопросы и задачи к лекции 7
- •Вопросы и задачи к лекции 8
- •Вопросы и задачи к лекции 9
- •Вопросы и задачи к лекции 10
- •Вопросы и задачи к лекции 11
- •Вопросы и задачи к лекции 12
- •Вопросы и задачи к лекции 13
- •Вопросы и задачи к лекции 14
- •Вопросы и задачи к лекции 15
- •Вопросы и задачи к лекции 20
- •Вопросы и задачи к лекции 21
- •Вопросы и задачи к лекции 22
- •Вопросы и задачи к лекции 23
- •Вопросы и задачи к лекции 24
- •Вопросы и задачи к лекции 25
- •Вопросы и задачи к лекции 28
- •Вопросы и задачи к лекции 29
- •Вопросы и задачи к лекции 30
- •Вопросы и задачи к лекции 31
Вопросы и задачи к лекции 28
294-1. Для каких электростатических систем применим метод разделения переменных?
295-2. Назовите 4 главных этапа (момента) метода разделения переменных.
296-3.
Проиллюстрируйте 4 главных этапа метода
разделения переменных на примере задачи
расчета поля диэлектрического цилиндра
(кругового сечения), помещенного в
заданное однородное поле
![]() .
.
297-4. Найдите потенциал диполя
298-5. Найдите потенциал линейного диполя.
299-6. Назовите преимущества метода интегральных уравнений по сравнению с другими методами.
300-7.
Получите интегральное уравнение для
расчета поля диэлектрического цилиндра
(не обязательно кругового) с проницаемостью
![]() ,
помещенного в диэлектрик с проницаемостью
,
помещенного в диэлектрик с проницаемостью
![]() ,
в котором существовало плоскопараллельное
поле
(поле
в каждой точке не зависит от координаты
вдоль образующей цилиндра и перпендикулярно
образующей цилиндра). Рассмотрите случай
кругового цилиндра и однородного поля
,
перпендикулярного оси цилиндра.
,
в котором существовало плоскопараллельное
поле
(поле
в каждой точке не зависит от координаты
вдоль образующей цилиндра и перпендикулярно
образующей цилиндра). Рассмотрите случай
кругового цилиндра и однородного поля
,
перпендикулярного оси цилиндра.
Вопросы и задачи к лекции 29
301-1. Запишите уравнения Максвелла в дифференциальной и интегральной формах для магнитного поля стационарных токов.
302-2. Запишите граничные условия на границе раздела двух сред для магнитного поля стационарных токов.
303-3. Получите дифференциальные уравнения и граничные условия для векторного потенциала магнитного поля стационарных токов.
304-4. Получите дифференциальные уравнения и граничные условия для скалярного магнитного потенциала магнитного поля стационарных токов.
305-5.
Как изменится постановка краевой задачи,
описанной в лекции, если вместо
![]() положить
положить
![]() ?
?
306-6. Сформулируйте теорему эквивалентности для магнитного поля стационарных токов.
307-7.
Бесконечно длинный круговой цилиндр
радиуса
расположен в поле прямолинейного
бесконечно длинного проводника с током
![]() (рис. 4.62). Проводник параллелен оси
цилиндра. Расстояние от проводника до
оси цилиндра
.
Магнитная проницаемость материала
цилиндра
.
Найдите магнитное поле
(рис. 4.62). Проводник параллелен оси
цилиндра. Расстояние от проводника до
оси цилиндра
.
Магнитная проницаемость материала
цилиндра
.
Найдите магнитное поле
![]() вне цилиндра методом зеркальных
отображений.
вне цилиндра методом зеркальных
отображений.

Рис. 4.62. Ферромагнитный цилиндр с в поле прямолинейного проводника с током
308-8. Решите предыдущую задачу методом интегральных уравнений.
Вопросы и задачи к лекции 30
309-1. Запишите дифференциальные уравнения внутри магнита для зарядовой модели. Как выражается плотность магнитного заряда внутри магнита через вектор намагниченности?
310-2. Выведите выражение для поверхностной плотности магнитного заряда на поверхности магнита.
311-3. Запишите дифференциальные уравнения внутри магнита для токовой модели. Как выражается плотность микротока внутри магнита через вектор намагниченности?
312-4. Выведите выражение для поверхностной плотности микротока на поверхности магнита.
313-5. Запишите формулы вычисления магнитного поля постоянно магнита тремя способами.
314-6.
Два бесконечно длинных цилиндрических
постоянных магнита намагничены однородно
вдоль своих осей, причем
![]() (рис. 4.69). Соединены магниты так, как
показано на рис. 4.69. Найдите поля
и
во всем пространстве.
(рис. 4.69). Соединены магниты так, как
показано на рис. 4.69. Найдите поля
и
во всем пространстве.
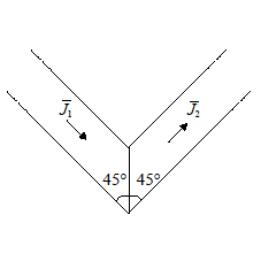
Рис. 4.69. Два цилиндрических постоянных магнита
315-7. Какое поле называют квазистационарным?
316-8. Найдите выражение для поля внутри проводника, на который падает монохроматическая линейно поляризованная электромагнитная волна.
317-9. Найдите выражение для поля внутри проводника, на который падает монохроматическая линейно поляризованная электромагнитная волна.
318-10. Дайте определение и запишите выражение для глубины проникновения электромагнитного поля внутрь проводника.
319-11. Получите граничное условие Леонтовича.
