Задание 6.

Использование условных операторов и операторы цикла при вычислении чисел Фибоначчи.

Любая более или менее серьёзная программа подразумевает использование управляющих инструкций, среди которых особое место занимают условные операторы и операторы циклов. Рассмотрим особенности применения таких операторов.

Общий принцип действия условного оператора заключается в следующем: проверяется условие, и если оно истинно - выполняется последовательность операций (цикл с предусловием). Также можно определить последовательность действий в случае если условие ложно (цикл с постусловием, выполняется до истинности условия).

Оператор цикла позволяет выполнять последовательности однотипных действий.

1) Создадим с помощью оператора цикла FOR макрос, который заполняет ячейки документа числами Фибоначчи (по имени средневекового математика Леонардо Пизанского, известного как Фибоначчи):

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

Числами Фибоначчи называют последовательность натуральных чисел, первые два из которых равны 1, а каждое последующее равно сумме двух предыдущих.

Примечание 3: Оказывается, эта последовательность имеет множество интересных с точки зрения математики свойств. Вот пример: вы можете разделить линию на два сегмента, так что соотношение между большим и меньшим сегментом будет пропорционально соотношению между всей линией и большим сегментом. Этот коэффицент пропорциональности, приблизительно равный 1,618, известен как золотое сечение. В эпоху Возрождения считалось, что именно эта пропорция, соблюденная в архитектурных сооружениях, больше всего радует глаз. Если вы возьмете последовательные пары из ряда Фибоначчи и будете делить большее число из каждой пары на меньшее, ваш результат будет постепенно приближаться к золотому сечению. Другую интересную информацию о числах Фибоначчи можно найти в Интернете: http://elementy.ru/trefil/21136; http://ru.wikipedia.org и др..

Также, в оператор For добавим условный оператор, с помощью которого обеспечим необходимость того, чтобы числами ячейки заполнялись только в том случае, если в активную ячейку введено число большее 2. В VBA существует условный оператор If…. Then….Else, который реализует означенный алгоритм. Программный код данного макроса приведен в листинге 18:

Листинг 18: Программный код макроса Fibon ( )

Public Sub Fibon ( )

Dim N As Integer

Dim i As Integer

Dim a As Integer

Dim b As Integer

N = ActiveCell.Value

If N<2 Then

MsgBox Prompt: = “Указано неверное значение!”, Title: = “Ошибка!”

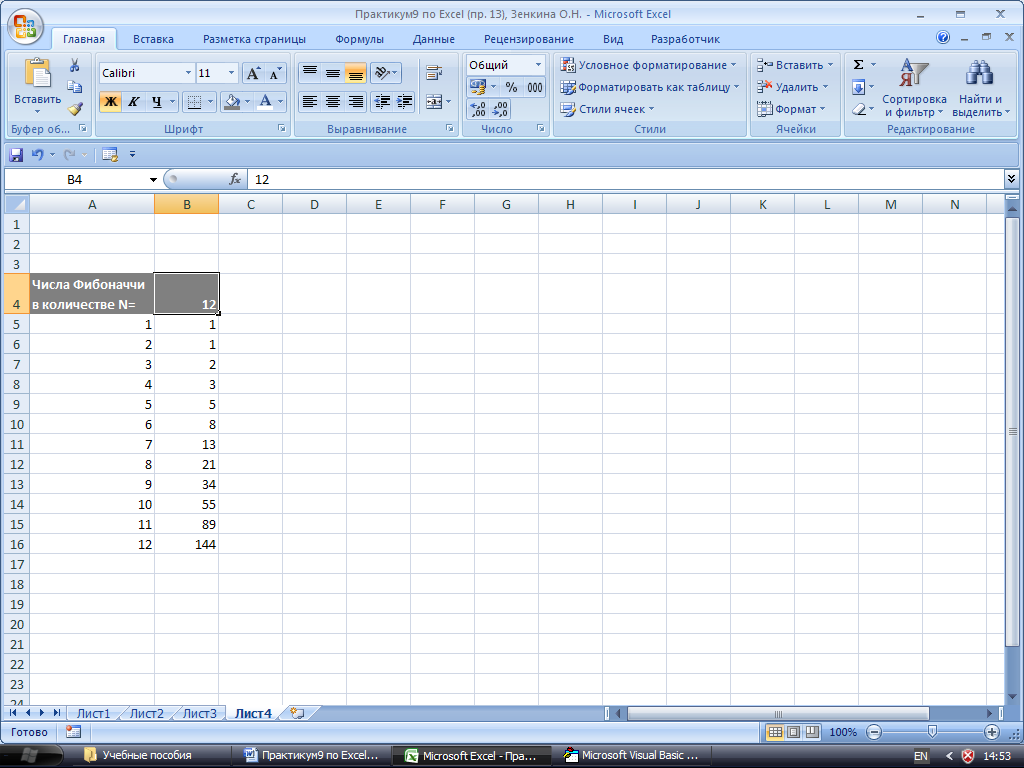E lse

a = 1

ActiveCell.Offset(1,-1).Value = 1

ActiveCell.Offset(1,0).Value = a

b = 1

For i = 2 To N

ActiveCell.Offset(i,-1).Value = i

ActiveCell.Offset(i,0).Value = b

b = b + a

a = b – a

Next i

End If

End Sub

Рис. 26. Результат выполнения задания 6, п. 1.

В ячейку А4 введите слова: «Числа Фибоначчи в количестве N = », в ячейку В4 введите число 12 (сколько чисел Фибоначчи будет выведено с помощью макроса), далее выделите ячейку B4 со значением 12 (ячейка B4 станет активной) и далее запустите макрос на выполнение. Результат выполнения макроса будет выглядеть как на рис. 27. Внизу, под ячейкой B4 (в ячейках B5:В16) будут выведены 12 чисел Фибоначчи. Поэкспериментируйте сами, с выполнением данного макроса, задавая для вычисления разное число чисел Фибоначчи в ячейке B4.

Если в ячейку В4 будет введено число меньшее 2, то результат будет иным, см. рис. 27:

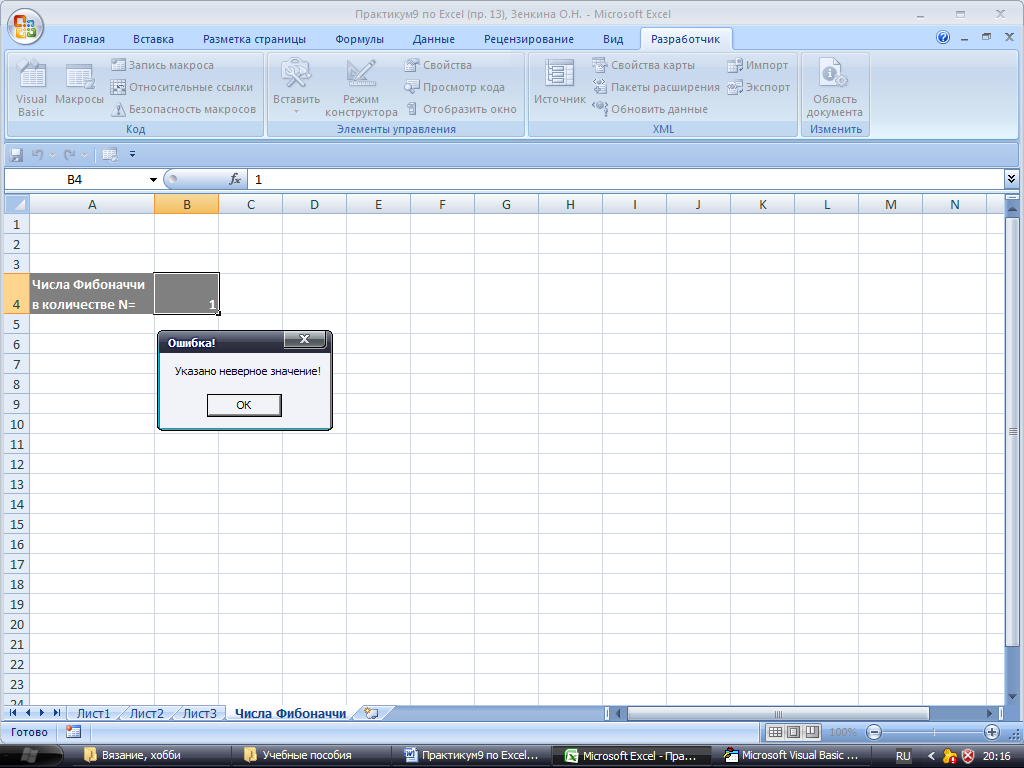
Рис. 27. Результат работы макроса при неверно указанном значении ячейки.

Данный макрос Fibon имеет недостатки, в частности не может вывести одно число Фибоначчи, когда значение в активной ячейке равно 1, а также не может обработать случай, когда в ячейка В4 содержит нечисловое значение.

Приведённый ниже макрос Fibon2 решает эти проблемы (см. листинг 19):