
- •2.1 Анализ расчета цепей постоянного тока с одним источником эдс (вопрос 14)
- •5.3 Переходные процессы в цепи с последовательным соединением резистивного, индуктивного и емкостного элементов (вопрос 60)
- •2.1.7 Параллельное соединение резистивного, индуктивного и емкостного элементов в цепи однофазного синусоидального тока (вопрос 27)
- •Раздел 5 Магнитные цепи
- •Тема 1. Магнитные цепи постоянного потока
- •9.2 Анализ неразветвленных магнитных цепей (вопрос 63)
- •9.4 Анализ разветвленных магнитных цепей (вопрос 64)
- •Тема 2. Магнитные цепи переменного потока
- •9.5 Особенности электромагнитных процессов в магнитных цепях переменного потока (вопрос 65)
- •9.6 Влияние немагнитного зазора в магнитопроводе при синусоидальном потоке (вопрос 66)
- •9.7 Полное уравнение электрического состояния и схема замещения обмотки при синусоидальном потоке (вопрос 67)
2.1.7 Параллельное соединение резистивного, индуктивного и емкостного элементов в цепи однофазного синусоидального тока (вопрос 27)
П
усть
к выводам электрической цепи (рисунок
6) приложено синусоидальное напряжение
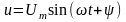 .
Мгновенное значение тока определим по
первому правилу Кирхгофа
.
Мгновенное значение тока определим по
первому правилу Кирхгофа
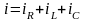 .
.
Рисунок 6 − Параллельное соединение -элементов
Известно,
что ток
 в сопротивлении
совпадает по фазе с напряжением
в сопротивлении
совпадает по фазе с напряжением
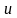 ,
ток
,
ток
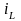 в индуктивности
отстаёт, а ток
в индуктивности
отстаёт, а ток
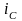 в ёмкости
в ёмкости
 опережает напряжение по фазе на угол
опережает напряжение по фазе на угол
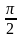 .
.
Суммарный ток в цепи равен

где
− полная реактивная проводимость цепи,
которая вычисляется по формуле,
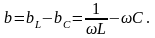 Уравнение представляет тригонометрическую
форму записи первого правила Кирхгофа
для мгновенных значений токов и
напряжений.
Уравнение представляет тригонометрическую
форму записи первого правила Кирхгофа
для мгновенных значений токов и
напряжений.
Если
полная реактивная проводимость цепи
 ,
то цепь носит индуктивный характер,
если
,
то цепь носит индуктивный характер,
если
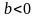 − емкостной характер. Активная
проводимость
− емкостной характер. Активная
проводимость
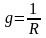 всегда положительна.
всегда положительна.
Амплитудное
значение тока можно записать как
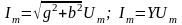 ,
где
,
где
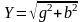 − модуль полной проводимости
рассматриваемой цепи. Действующее
значение тока имеет следующий вид
− модуль полной проводимости
рассматриваемой цепи. Действующее
значение тока имеет следующий вид
 .
.
Угол
сдвига фаз между током
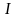 и напряжением
и напряжением
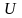 равен
равен
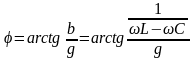 .
.
Если
задано напряжение
на выводах цепи с параллельно соединенными
 элементами, то ток будет определяется
по следующей формуле
элементами, то ток будет определяется
по следующей формуле
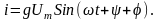
Угол
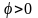 при индуктивном характере цепи, т.е. при
полной проводимости цепи
,
при этом ток отстает по фазе от напряжения.
Угол
при индуктивном характере цепи, т.е. при
полной проводимости цепи
,
при этом ток отстает по фазе от напряжения.
Угол
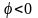 при емкостном характере цепи, т. е. при
,
при этом ток опережает по фазе напряжение.
при емкостном характере цепи, т. е. при
,
при этом ток опережает по фазе напряжение.
Ток
совпадает с напряжением по фазе при
 ,
т. е. при равенстве индуктивной и емкостной
проводимостей. Такой режим работы
электрической цепи называется резонансом
тока.
,
т. е. при равенстве индуктивной и емкостной
проводимостей. Такой режим работы
электрической цепи называется резонансом
тока.
Если
выразить активную проводимость как
 ,
а реактивную проводимость как
,
а реактивную проводимость как
 ,
то активная составляющая тока запишется
как
,
то активная составляющая тока запишется
как
 ,
а реактивная составляющая тока −
,
а реактивная составляющая тока −
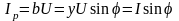 .
.
Тогда
действующее значение суммарного тока,
или модуль тока имеет вид
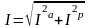 .
.
Рассмотрим случай для участка, напряжение на котором равно
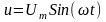 ,
а ток равен
,
а ток равен
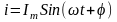 .
.
Мгновенная мощность, поступающая в цепь
 состоит
из двух слагаемых: постоянной величины
состоит
из двух слагаемых: постоянной величины
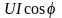 и синусоидальной, имеющей удвоенную
частоту по сравнению с частотой напряжения
и тока.
и синусоидальной, имеющей удвоенную
частоту по сравнению с частотой напряжения
и тока.
Активная мощность, поступающая в цепь равна
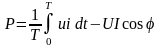 .
.
Множитель
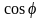 носит название коэффициента мощности.
носит название коэффициента мощности.
Активная мощность равна произведению действующих значений напряжения и тока, умноженному на коэффициент мощности.
Чем
ближе угол
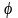 к нулю, тем ближе
к единице и, следовательно, тем больше
при заданных значениях
и
активная мощность передаётся источником
приемнику.
к нулю, тем ближе
к единице и, следовательно, тем больше
при заданных значениях
и
активная мощность передаётся источником
приемнику.
Выражения для активной мощности может быть преобразовано следующим образом:
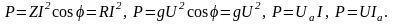
Выражение для реактивной мощности можно записать в виде:
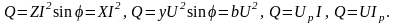
Очевидно,
что
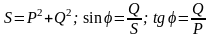 .
.
2.3.3 Законы Ома и Кирхгофа в комплексной форме. Параллельное соединение R,L,C элементов
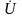
Рассмотрим электрическую цепь на рисунке 15.
Рисунок 15 – Параллельное соединение -элементов
Запишем первое правило Кирхгофа для этой цепи
 ,
,
где
 ток в сопротивлении
(ток совпадает по фазе с напряжением);
ток в сопротивлении
(ток совпадает по фазе с напряжением);
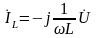 ток индуктивности (ток отстаёт от
напряжения на угол
);
ток индуктивности (ток отстаёт от
напряжения на угол
);
 –
ток в ёмкости (ток опережает напряжение
на угол
).
–
ток в ёмкости (ток опережает напряжение
на угол
).
Формула
для определения комплексной проводимости
запишется
 ,
где
,
где
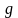 – активная,
– реактивная проводимости.
– активная,
– реактивная проводимости.
Запишем
закон Ома в комплексной форме
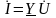 ,
,
где
 или
или
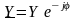 ,
где
,
где
 – модуль комплексного числа, а
– модуль комплексного числа, а
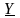 – полная проводимость цепи равная
– полная проводимость цепи равная
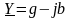 ,
а
,
а
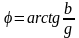 – сдвиг фаз в цепи.
– сдвиг фаз в цепи.
П остроим
векторные диаграммы. Рассмотрим
электрическую цепь, у которой проводимость
имеет индуктивный характер, т. е.
и
(рисунок 16).
остроим
векторные диаграммы. Рассмотрим
электрическую цепь, у которой проводимость
имеет индуктивный характер, т. е.
и
(рисунок 16).
Рисунок 16 – Векторная диаграмма
Для случая когда реактивная проводимость имеет емкостной характер, т. е. , , векторная диаграмма представлена на рисунке 17.

Рисунок 17 – Векторная диаграмма
Н арисуем
треугольник проводимостей для двух
случаев. Если полная проводимость цепи
и полная проводимость цепи
(рисунок 18):
арисуем
треугольник проводимостей для двух
случаев. Если полная проводимость цепи
и полная проводимость цепи
(рисунок 18):
Рисунок 18 – Треугольники проводимостей
