
- •Гармонический анализ
- •§1. Периодические функции.
- •Примеры из фэпо.
- •§2. Гармонические колебания.
- •Примеры из фэпо
- •§ 3. Тригонометрические ряды. Ряды Фурье. Основные понятия. Разложение в ряд Фурье функций с периодом 2.
- •Ряд Фурье в виде простых гармоник. Спектры.
- •§ 4. Разложение в ряд Фурье четных и нечетных функций периода 2.
- •Решение:
- •§ 5. Сдвиг основного промежутка.
- •Решение:
- •§ 6. Разложение в ряд Фурье функций с периодом 2ℓ.
- •Решение:
- •Решение:
- •§ 7. Разложение в ряд Фурье функций, заданных на полупериоде.
- •Решение:
- •§ 8. Разложение в ряд Фурье функций с “двойной симметрией”.
- •§ 9. Интеграл Фурье.
- •2.1. Интеграл Фурье и двойной интеграл Фурье.
- •Решение:
- •2.2. Интеграл Фурье для четных и нечетных функций.
- •Решение:
- •Решение:
- •2.3. Комплексная форма интеграла Фурье.
- •Решение:
§ 3. Тригонометрические ряды. Ряды Фурье. Основные понятия. Разложение в ряд Фурье функций с периодом 2.
Определение 7. Функциональный ряд вида:
![]() +
+
![]() (
ancos
nx + bnsin
nx )
(1)
(
ancos
nx + bnsin
nx )
(1)
называется тригонометрическим, причем an и bn – действительные числа, не зависящие от x.
Пусть y = f(x) – произвольная периодическая функция с периодом Т = 2, следовательно, функцию можно рассматривать в любом интервале длины 2, например, (–; ). На других участках оси (Ох) функция f(x) и ее разложение в ряд будет повторять свои значения и свое поведение в основном интервале.
Предположим, что для любого x(–; ) периодическая функция оказалась такой, что для нее нашлось разложение в равномерно сходящийся ряд указанного вида:
f(x)
=
![]() +
(
akcos
kx + bksin
kx ) (
1.1)
+
(
akcos
kx + bksin
kx ) (
1.1)
Такое представление дает возможность находить численные значения функции, устанавливать различные свойства функций, решать дифференциальные уравнения и т.п.
Получим формулы для вычисления коэффициентов ak и bk. Проинтегрируем почленно данное равенство в пределах от – π до π (законное в силу предложенной сходимости):
![]() .
(1.2)
.
(1.2)
Вычислим отдельно следующие интегралы:
если n – целое,
![]()
![]() (1.3)
(1.3)
![]()
![]() (1.4)
(1.4)
если n, m – целые, положительные
![]()
![]() (1.5)
(1.5)
![]() =
(1.6)
=
(1.6)
![]() .
(1.7)
.
(1.7)
С учетом формул (1.3) и (1.4) почленное интегрирование равенства (1.2) дает:
![]() (1.8)
(1.8)
Умножая (1.1) на cos nx и интегрируя почленно от – π до π, с учетом (1.3), (1.5), (1.7), получим:
![]() (1.9)
(1.9)
Аналогично, умножая (1.1) на sin nx и интегрируя почленно от – π до π и учитывая (1.4), (1.6), (1.7), получим:
![]() (1.10)
(1.10)
Таким образом, из равенств (1.8), (1.9), (1.10) получим выражения для нахождения коэффициентов.
Теорема 1. Если функция f(x), заданная и непрерывная на отрезке [-; ], разлагается в тригонометрический ряд, то коэффициенты его определяются единственным образом.
Определение 8. Пусть f(x) – произвольная функция с периодом 2, заданная в интервале (–; ). Пусть существует интеграл от данной функции в интервале (–; ), при этом f(x) может иметь конечное число точек разрыва 1-го рода. Рядом Фурье этой функции называется ряд
![]() +
+![]()
коэффициенты которого определяются по формулам:
а0
=
![]() ;
( 1.11)
;
( 1.11)
аn
=
![]() (n =1,2,...); ( 1.12 )
(n =1,2,...); ( 1.12 )
bn =
![]() (n =1,2,...). ( 1.13 )
(n =1,2,...). ( 1.13 )
Замечание 1. Для вычисления интегралов потребуются следующие формулы:
![]() для любого n,
для любого n,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Из определения ряда Фурье не следует, что функция должна в него разлагаться. Из сказанного выше следует следующая теорема:
Теорема 2 (единственности). Если непрерывная на [-; ] функция разлагается в равномерно сходящийся тригонометрический ряд, то этот ряд будет обязательно ее рядом Фурье.
Замечание 2. Исходя из теоремы, в определении можно рассматривать не интервал (–; ), а отрезок [–; ].
Функция f(x) не всегда разлагается в свой ряд Фурье, т.е. является его сумой, даже если он сходится, а лишь тогда, когда она удовлетворяет условиям основной теоремы:
Теорема 3 (основная). Если
функция f(x)
кусочно-гладкая на отрезке [-;
], то
ее ряд Фурье сходится к функции f(x)
во всех точках, в которых она непрерывна.
В точках разрыва функции f(x)
ряд сходится к среднему арифметическому
ее предельных значений слева и справа,
т.е. к значению
![]() ,
где
,
где
![]() –
точка разрыва 1-го рода. В обеих граничных
точках интервала сумма ряда равна
среднему арифметическому предельных
значений функции при стремлении
независимой переменной к этим точках
изнутри интервала
–
точка разрыва 1-го рода. В обеих граничных
точках интервала сумма ряда равна
среднему арифметическому предельных
значений функции при стремлении
независимой переменной к этим точках
изнутри интервала
![]() (без
доказательства).
(без
доказательства).
Замечание. Функция называется гладкой в интервале, если в этом интервале она непрерывна вместе со своей первой производной. Функция называется кусочно-гладкой в интервале, если данный интервал можно разбить точками разрыва 1-го рода на конечное число интервалов, в каждом из которых функция гладкая.
Следствие теоремы.
Теорема гарантирует разложимость всякой
дифференцируемой на отрезке [–;
]
функции в ее ряд Фурье не на всем этом
отрезке, а лишь на открытом промежутке
(–;
),
однако если разлагаемая функция
удовлетворяет еще дополнительному
условию, что
![]() ,
то она будет представима своим рядом
Фурье на всем отрезке [–;
].
,
то она будет представима своим рядом
Фурье на всем отрезке [–;
].
Существуют и иные достаточные признаки разложимости функций в ряд Фурье, например, следующая теорема:
Теорема 4 (Дирихле).
Если функция f(x) имеет на интервале (-; ) лишь конечное число максимумов и минимумов и непрерывна, за исключением, м.б., конечного числа точек разрыва 1-го рода, то f(x) разлагается в ряд Фурье, сходящийся в точках непрерывности к самой функции, а в точках ее разрыва – к значению . (без доказательства)
В силу основной теоремы, если ряд является рядом Фурье функции f(x), можно написать:
f(x)
=
![]() +
(
ancos
nx + b
nsin
nx )
( 1.14 )
+
(
ancos
nx + b
nsin
nx )
( 1.14 )
Пример 1: Разложить в ряд Фурье функцию с периодом 2:
f(x)
=
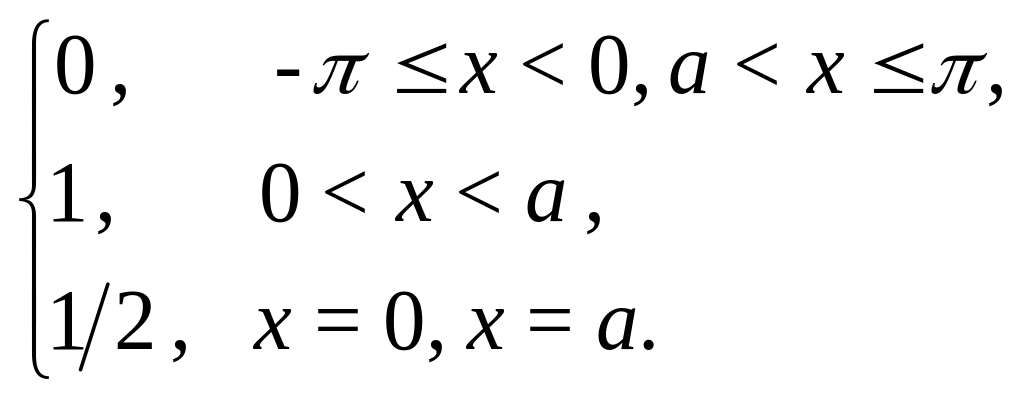
Решение:
Из определения f(x) следует, что она удовлетворяет условиям теоремы о разложимости в ряд Фурье, поэтому f(x) разлагается в ряд Фурье. (См. рис. 1.)

Рис. 1.
По формулам (1.11)-(1.13) находим коэффициенты Фурье:
а0 =
![]() =
=
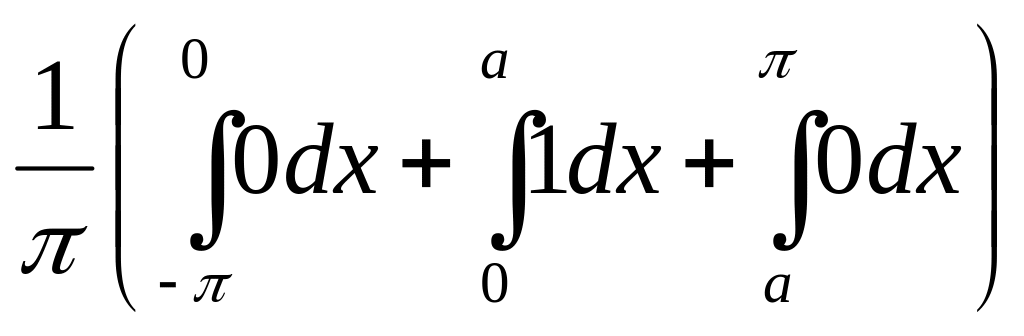 =
=
![]() =
а/.
=
а/.
аn
=
=
![]() =
=
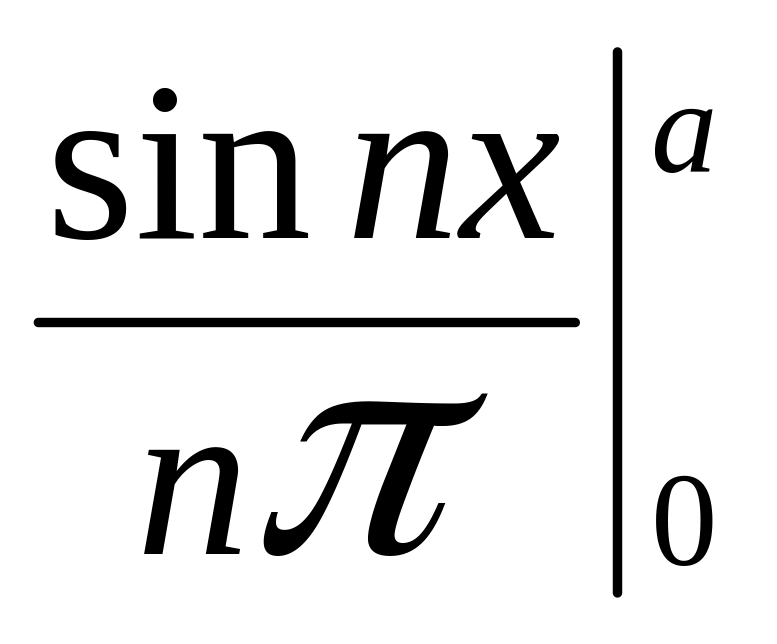 =
=
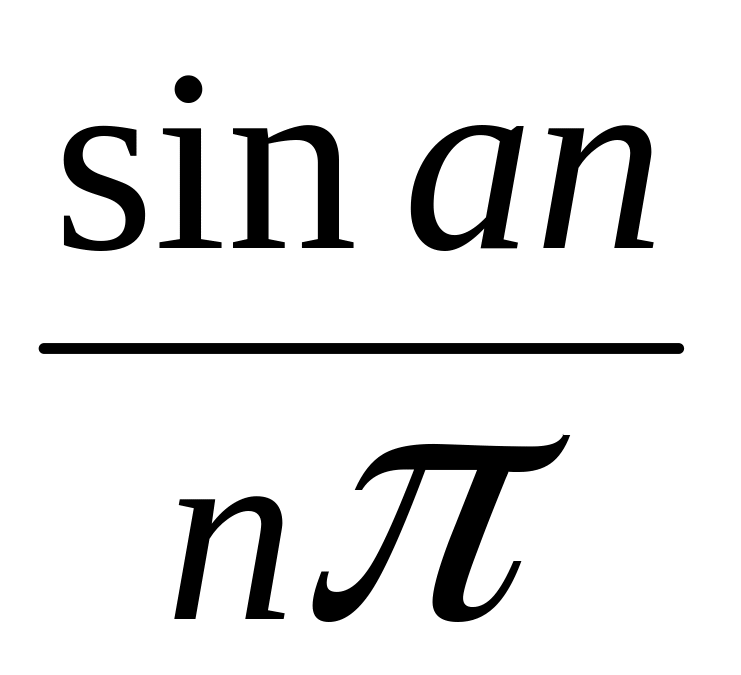 , при n
0.
, при n
0.
Замечание.
Если n = 0, то для вычисления аn поступаем следующим образом: рассмотрим предел при n0
![]() =
=
![]()
![]()
![]() =
=![]() =
,
=
,
bn =
=![]() =
–
=
–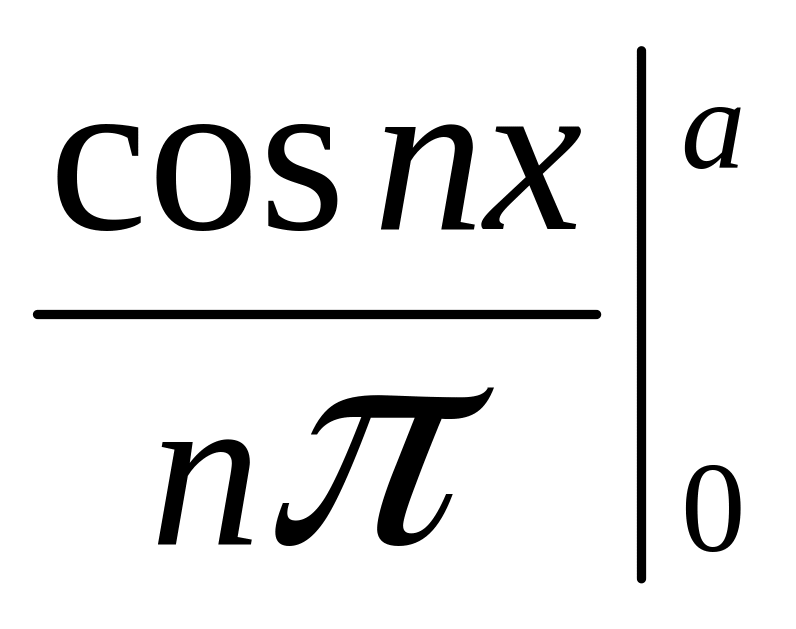 =
–
=
–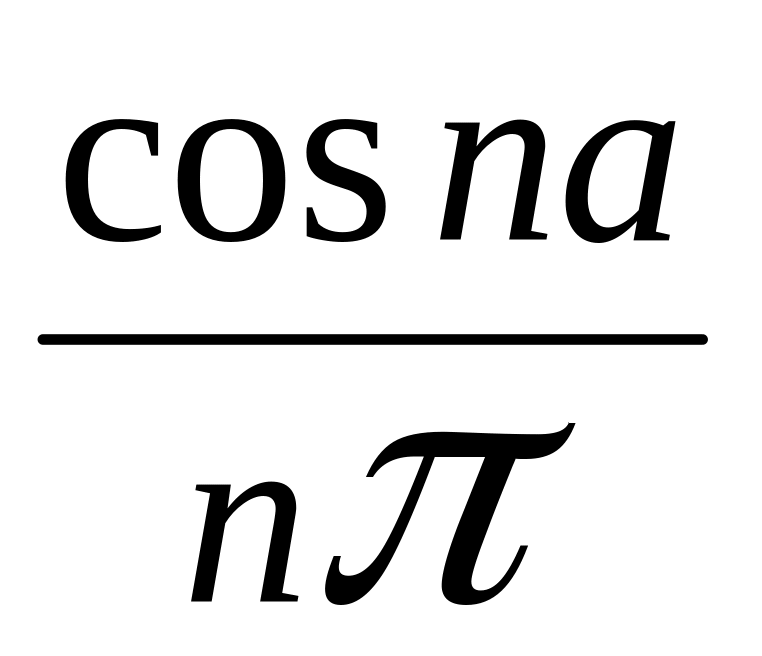 +
+![]() =
= ,
при n
0.
,
при n
0.
Следовательно,
f(x)
=
![]() .
.
В интервале [-; ] ряд сходится к функции f(x), в точках х = к 0: ( 1/2 [ f(–+0) + f(–0)] = 0 ), в точках х = a, x = 0 к 1/2 : ( 1/2 [ f(х-0) + f(х+0)] = =1/2 ).
