4. Функціональні ряди

Визначення 1. Ряд називається функціональним, якщо члени його є функціями від .

Розглянемо функціональний ряд

+ + + …… + …...= (4.1)

Надаючи змінній деяке значення , одержимо числовий ряд

+ + + …… + …...= (4.2)

Якщо ряд (4.2) сходиться, то точка називається точкою збіжності функціонального ряду.

Визначення 2. Сукупність всіх точок збіжності функціонального ряду називається його областю збіжності.

Якщо значення є точка збіжності ряду (4.1), то можна говорити про суму ряду (4.2). Сума функціонального ряду є функція . Областю визначення функції буде область збіжності ряду (4.1).

4.1 Степеневі ряди. Інтервал збіжності

Визначення 3. Степеневим рядом називається функціональний ряд виду

(4.3)

де , , , …- постійні числа, які називаються коефіцієнтами ряду.

Області збіжності степеневих рядів описуються наступною теоремою.

Теорема 4.1. (Теорема Абеля) Якщо степеневий ряд (4.3) збігається при деякому = , те він збігається абсолютно при всіх значеннях , для яких .

Якщо ряд (4.3) розбігається при = , то він розбігається при всіх значеннях , для яких

Теорема Абеля приводить до наступного твердження: існує таке , що при ряд (4.3) розбігається, при - збігається, а поведінка ряду при підлягає подальшому аналізу. Множина значень змінної , задовольняючому співвідношенню називається інтервалом збіжності ряду (4.3), а число R – радіусом збіжності цього ряду.

Радіус збіжності статечного ряду можна знаходити по формулі

(4.4)

Приклад1. Визначити інтервал збіжності степеневого ряду й дослідити збіжність ряду на кінцях інтервалу.

Складемо ряд з модулів і дослідимо його за ознакою Даламбера

Для даного ряду

;

Тоді

Даний ряд збігається абсолютно, якщо <1, тобто <1;

, - радіус збіжності.

Дослідимо збіжність ряду на кінцях інтервалу, тобто при

розбігається як гармонійний ряд

даний ряд не збігається абсолютно. Застосовуючи ознаку Лейбниця, одержимо, що ряд збігається умовно. Таким чином, ряд збігається на проміжку .

Приклад2. Визначити інтервал збіжності степеневого ряду й дослідити збіжність ряду на кінцях інтервалу.

Складемо ряд з модулів і дослідимо його за ознакою Даламбера

Для даного ряду

;

Тоді

Даний ряд збігається абсолютно при будь-яких значеннях .Таким чином, область збіжності даного ряду

4. Ряди тейлора й маклорена

5.1 Розклад функції в ряд Тейлора

Якщо функція нескінченно диференційована в точці , то її в околиці цієї точки можна представити степеневим рядом, який називають рядом Тейлора:

(5.1)

Зокрема, при =0 одержуємо ряд Маклорена:

(5.2)

Розклад в ряд Маклорена функцій , , , , називають основними розкладами:

= ,

= ,

= ,

,

,

,

,

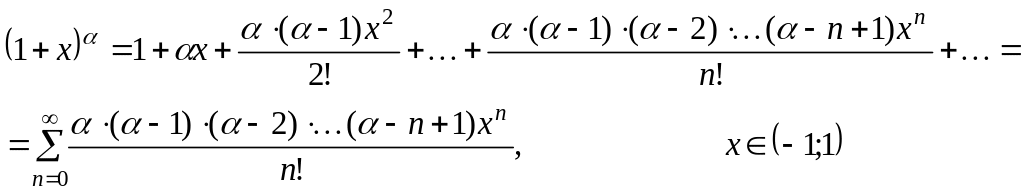
Якщо потрібно розкласти в ряд Тейлора довільну функцію, то можна скористатися формулами (5.1) і (5.2). Однак для багатьох функцій розклад в ряд Тейлора або Маклорена можна одержати, користуючись відомими розкладами елементарних функцій.

Приклад1. Розкласти в ряд Тейлора в околиці точки функцію .

Рішення.

Скористаємося Формулою (5.1)

, , , ,

, … , , …

, , , ,

, … , , …

збігається, якщо -1< <1, тобто (0; 2) – інтервал збіжності.

Приклад2 Розкласти в ряд Тейлора в околиці точки (ряд Маклорена) функцію

Рішення.

Скористаємося біноміальним рядом

.

Приклад3. Представити у вигляді степеневого ряду (ряду Маклорена) функцію .

Рішення.

- інтервал збіжності.