5.2, Теплопровідність.

До сказаного в попередньому параграфі слід додати, що теплопровідність - це такий теплообмін, коли перенос теплової енергії в нерівномірно нагрітому середовищі проходить у відсутності макроскопічного руху середовища. У газах — це хаотичний рух молекул, у металах - це вільні електрони, у діелектриках - переважний механізм теплопровідності коливання атомів.

Теплопровідність може здійснюватися як всередині тверде :т> тіла, так і через гази чи рідини. Поширення теплоти теплопровідністю буде лише тоді, коли в різних точках середовища будуть різні температури. Для простоти будемо вважати, що маємо стаціонарний тепловий режим, коли температура у всіх точках з часом не змінна. Нестаціонарний режим характеризується зміною температури точок тіла з часом. Такий режим буде однозначним, коли тіло весь час нагрівається або охолоджується. Коли період нагрівання і охолодження чергуються, то такий режим буде коливним. Деякі процеси передачі теплової енергії супроводжуються перенесенням речовини (конвекція, променевий теплообмін), то ці питання вивчає теорія масообміну.

Для теплопровідності твердих тіл Фурьє встановив наступний закон:

(5.5)

Це є основним законом теплопровідності. Мінус тут значить, що вектори направлені в протилежні сторони.

- це фізичний параметр, який характеризує теплопровідність і називається коефіцієнтом теплопровідності.

• дорівнює густині теплового потоку через одношарову

стінку при температурному напорі 1 К.

Коефіцієнт м.ає високе значення для металів і мале для сухого повітря. Якщо . то матеріал буде теплоізолятором. До

теплоізоляторів відносять майже всі будівельні матеріали, а найкращим теплоізолятором є вакуум.

З підвищенням температури для будівельних і теплоізоляційних матеріалів зростає. Наприюгад, цегли в топці збільшується

приблизно в 3...4 рази проти відповідних значень на вільному повітрі. У більшості металів із збільшенням температури зменшується. Домішки у металах значно зменшують величину

Величина коефіцієнта пропорційна густині матеріалу, чим вища - густина матеріалу, тим краща у ньому теплопровідність. Пористість матеріалу сильно впливає на , тому що коефіцієнт повітря приблизно в 50 разів менший від інших будівельних матеріалів. Для пористих матеріалів теплопровідність знаходиться в оберненій залежності від їх загальної пористості і в прямій — від розмірів пор.

Для анізотропних матеріалів, які мають не однакову структуру в різних напрямках, теплопровідність залежить від напрямку теплового потоку. Так, наприклад, сосна в два рази краще проводить теплоту вздовж волокон, ніж поперек. Це пояснюється тим, що при напрямку, перпендикулярному волокнам, тепловому потоку доводиться пересікати велику кількість повітряних зазорів, які існують між волокнами і тим самим зростає термічний опір.

Таким чином, коефіцієнт теплопровідності залежить від властивостей матеріалу (густини, молекулярної будови, структури,, вологості), температури і в незначній мірі від тиску. Але в технічних розрахунках в більшості випадків його визначення для досліджуваного матеріалу приймають сталим, яке дорівнює середньоарифметичному в даних межах зміни температури. Для більшості матеріалів залежність коефіцієнта теплопровідності від температури наближено можна вважати лінійною: густиною. Із зростанням вологості матеріалу коефіцієнт

теплопровідності значно зростає. Так, для мокрої цегли ,

що перевищує значення коефіцієнта теплопровідності як для води, так і для сухої цегли. Підвищення тиску водяної пари при сталій температурі викликає збільшення . Найкращими провідниками теплоти є метали, для яких має значення від 20 до 450 . Коефіцієнт теплопровідності

чистих, металів, за виключенням алюмінію, з ростом тем;.ератури зменшується. В металах теплопровідність обумовлено тепловим рухом віїьних електронів («електронного газу»), які в три тисячі разів легші за молекули газів. Тому теплопровідність металів набагато більше, ніж газів. Найбільший коефіцієнт теплопровідності мають чисті срібло і мідь. Значення коефіцієнта теплопровідності найпоширеніших в побуті, шкільних майстернях матеріалів наведені в таблиці 5.1.

Мал.5.2. Залежність коефіцієнта теплопровідності від температури: 1-повітря; 2-3-мінеральна вата густиною 150 і 400 ; 4-червона цегла; 5-вода; 6-залізо;

7-латунь (67% Си, 33% Zn); 8-мідь; 9-срібло.

(5.6) де - значення коефіцієнта теплопровідності при температурі

- стала, яка визначається дослідним шляхом; - температура, при якій визначається

Найнижчий коефіцієнт теплопровідності мають гази, причому, він збільшується із зростанням температури і становить 0,06...0,6

Для краплинних неметалевих рідин = 0,07...0,7 і для більшості з

них зменшується при зростанні температури. Вода є одним з кращих рідких провідників теплоти. Коефіцієнт теп/юпровідності води із

збільшенням температури зростає до максимального значення

а потім зменшується при подальшому збільшенні температури.

Коефіцієнт теплопровідності теплоізоляційних і будівельних матеріалів, які мають пористу структуру, при підвищенні температури,

зростає за лінійним законом і змінюється в межах від 0,02 до 3,0

ЗбЬгьшення пористих матеріалів при зростанні температури

пояснюється значним зростанням променевого теплообміну між поверхнями твердого «скелета» пор. Роль конвекції в збільшенні зростає при збільшенні розмірів пор і відповідно повітряних включень. Тому ефективний коефіцієнт теплопровідності пористих тіл має складну природу і є умовною величиною. Крупнопористий матеріал буде менш ефективним тепло ізолятором, чим дрібнопористий матеріал з такою ж

Таблиця 5.1

Розглянемо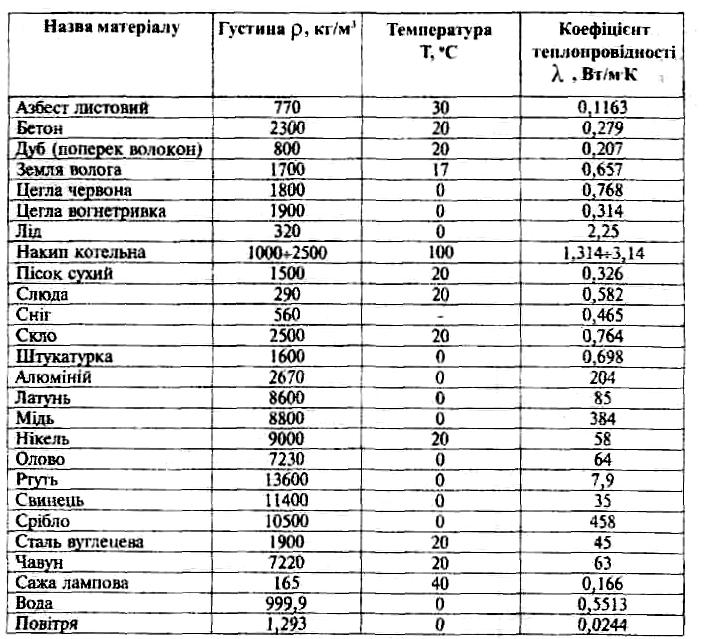 плоску одношарову стінку товщиною із однорідного матеріалу. Приймемо, що Температурне поле —

одномірне і поширення теплоти здійснюється лише в напряму х. Густину теплового потоку визначимо за формулою Фурьє, виділивши ізотермічними поверхнями шар dx:

Розділимо змінні і проінтегруємо:

Сталу інтегрування С визначимо із граничних умов при

Як випливає з попередньої формули, температура впоперек стінки змінюється зо лінійним законом.

Розрахункова формула густини теплового потоку для одношарової плоскої стінки має такий вигляд:

(5.7)

де - - теплова провідність стінки - тепловий опір стінки

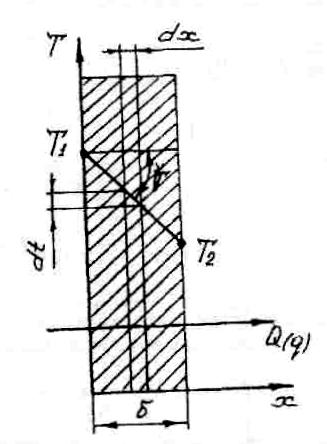
Рис.5.3. Стаціонарний розподіл температур по товщині плоскої стінки.

Густина теплового потоку пропорційна різниці температур І обернено пропорційна тепловому опору. Загальна кількість теплоти, що передається через стінку площею S за час становить: (5-8)

Згідно закону Відемана-Франца для всіх металів відношення коефіцієнта теплопровідності до питомої електропровідності прямо пропорційне температурі або:

(5-9)

де - стала Больцмана;

- заряд електрона;

- питома електропровідність.

Багатошарова плоска стінка найчастіше використовується в життєвій практиці (стінки котлів, печей, будинків і т.п.}. Нехай маємо стінки із трьох різнорідних матеріалів товщиною і

теплопровідністю Будемо вважати, що режим стаціонарний і

густина теплового потоку q. який проходить через кожен шар стінки, по величині однакова.

Для кожного із шарів можна записати (рис.5.4):

Для визначення повного перепаду температур додамо праві і ліві частини всіх трьох рівнянь, внаслідок чого будемо мати:

Звідси густина теплового потоку буде становити:

(5.10)

Таким чином, густина теплового потоку для багатошарової плоскої стінки пропорційна температурному напору і обернено пропорційна сумі термічних опорів всіх складових стінки.

В середині кожного шару температура змінюється прямолінійно. а нахил лінії Т залежить від величини коефіцієнта теплопровідності для кожної із стінок. Причому, чим нижче значення тим крутішим буде характер зміни температури поперек стінки.

Розглянемо циліндричну одношарову стінку. Нехай температура буде змінюватися лише вздовж радіуса, а по довжині труби І по її периметру залишається незмінною. В даному випадку тоді

рівняння Фур'є набирає вигляду:

(5.11)

Інтегрувати (5.11) не зручно, оскільки площа через яку

проходить тепловий потік, залежить від

Рис.5.4. Розподіл температури по товщині багатошарової плоскої стінки.

Рис.5.5. Розподіл температури по товщині одношарової циліндричної стінки.

Інтегруваннярівняння (5.12) дає:

Коли радіус зростає, тозменшується, а відповідно і

температура буде зменшуватися.

Розподіл температур по радіусу стінки підлягає логарифмічному закону (біля внутрішньої стінки вона змінюється крутіше). Про інтегруєморівняння 5.12 в певних межах

Для певного теплового потоку через багатошарову циліндричну стінку додають термічні опори кожної із складових.

1 зрештою доцільно розглянути кульову стінку. При постійних на

внутрішній і зовнішній поверхнях кульової стінки температурне поле одномірне в сферичних коороинатах, тобто температура змінюється тільки в напрямку Тоді тепловий потік становить:

Розділивши змінні і проінтегрувавши від маємо:

На відміну від циліндра і пластини теплова ізоляція, покладена на кулю безмежної товщини не виключає теплових втрат від неї навіть в

стаціонарному режимі.