41

1. Вырожденное распределение.

Говорят, что случайная величина имеет вырожденное распределение в точке a R, если принимает единственное значение a с вероятностью 1, т.е. P( =a)=1.

Данное распределение также называют причинным.

Функция распределения имеет вид

F (x) = P ( <x) =P(a<x) =

2.Распределение Бернулли.

Распределение часто используется при контроле качества продукции.

Говорят, что случайная величина имеет распределение Бернулли с параметром p , если принимает значения 1 и 0 с вероятностями p и 1-p=q соответственно. Случайная величина с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха p : ни одного успеха или один успех. Таблица распределения имеет вид:

3.Биноминальное распределение.

Распределение часто используется при контроле качества продукции, когда объем партии (генеральной совокупности) многократно превышает объем контрольной выборки n.

Для биномиального распределения вероятность принятия случайной величиной Y значения y определяется формулой

  

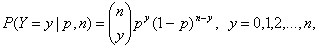
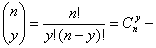
где

число сочетаний из n элементов по y, известное из комбинаторики.

Для всех y, кроме 0, 1, 2, …, n, имеем P(Y=y)=0.

4. Распределение Паскаля.

Распределение часто используется при контроле качества продукции.

Функция вероятности имеет вид:

5. Геометрическое распределение.

Геометрическое распределение достаточно популярно, в частности, при разработке математических методов контроля качества промышленной продукции.

Говорят, что случайная величина имеет геометрическое распределение с параметром , если принимает значения k=1,2,3,… с вероятностями . Случайная величина с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха p. Таблица распределения имеет вид

или

6.Гипергеометрическое распределение.

Широко используется при статистическом контроле качества продукции и выборочных обследованиях.

Для гипергеометрического распределения вероятность принятия случайной величиной Y значения y имеет вид:

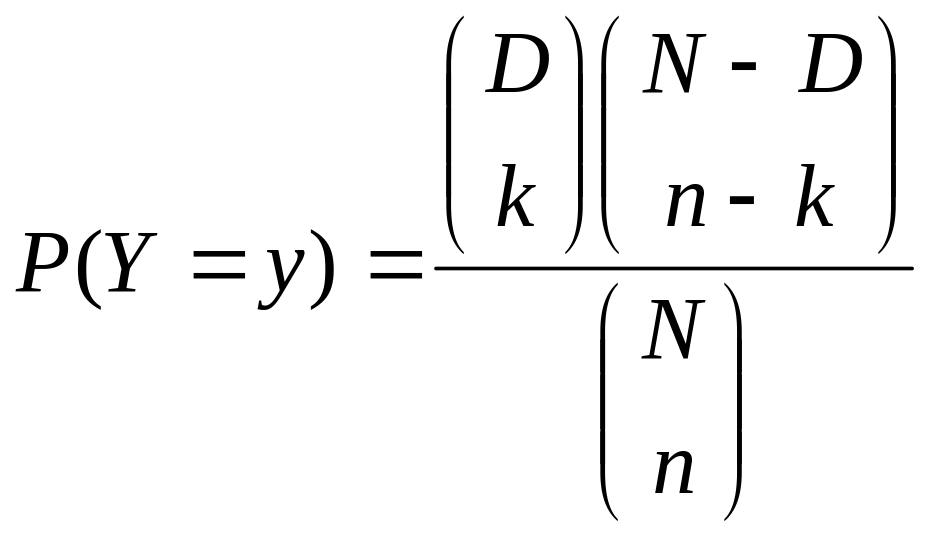
7. Распределение Пойе.

Этот закон также находит важные применения при статистических исследованиях заболеваний - эпидемий.

Плотность вероятности случайной величины имеет вид:

где , ,

8. Распределение Пуассона.

Случайная величина имеет распределение Пуассона, если принимает значения k=0,1,2,… с вероятностями

,где λ>0 – параметр распределения Пуассона.

9. Логарифмическое распределение.

Функция вероятности имеет вид:

10. Распределение Бореля-Таннера.

Дискретное распределение вероятностей случайной величины ξ, принимающей значения с вероятностями

где r > 0 — целое и 0 < α < 1.

11. Равномерное распределение.

Непрерывная случайная величина , принимающая значения на отрезке [a, b], распределена равномерно на [a, b], если ее плотность распределения p (x)

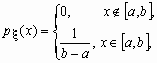
12. Распределение Симпсона.

Cлучайная величина ξ имеет треугольное распределение (распределение Симпсона) на отрезке [a,b] (a < b), если

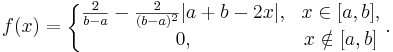
13. Показательное (экспоненциальное) распределение.

Широко используется в задачах теории массового обслуживания.

Непрерывная случайная величина имеет показательное распределение с параметром > 0, если она принимает только неотрицательные значения, а ее плотность распределения p (x ) имеет соответственно вид:

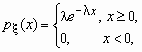
14. Нормальное распределение

Широко используется в статистических обследованиях, как эталонное распределение.

Случайная величина нормально распределена с параметрами a и , >0, если ее плотность распределения p (x )

15.Гамма - распределение.

Широко используется в статистических обследованиях, как эталонное распределение.

Случайная величина имеет Г-распределение (гамма-распределение) с параметрами a и b, если ее функция плотности вероятностей имеет вид:

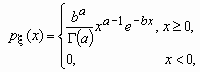, a > 0, b > 0,

16. Бета-распределение.

Широко используется в статистических обследованиях, как эталонное распределение.

Случайная величина имеет В-распределение (бета-распределение) с параметрами и , если ее функция плотности вероятностей имеет вид:

17. Распределение Коши.

Случайная величина имеет распределение Коши с параметрами и , если ее функция распределения имеет вид:

18. Распределение Лапласа.

Этот закон находит важные применения при статистических исследованиях.

Случайная величина имеет распределение Лапласа (двустороннее экспоненциальное распределение) с параметром и , если ее функция плотности вероятностей имеет вид:

19. Распределение хи-квадрат ( ²- распределение)

Этот закон находит важные применения при статистических исследованиях. По закону распределения ² распределена так называемая статистическая дисперсия, т. е. статистическая оценка дисперсии.

Плотность вероятности этой случайной величины вычисляется по формуле:

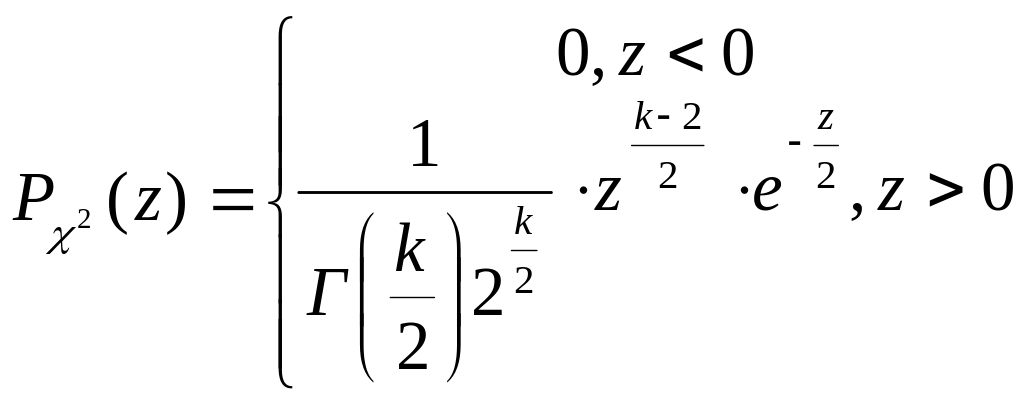
Здесь - гамма-функция Эйлера.

20. Распределение хи ( - распределение)

Плотность вероятности равна:

, x>0

21. F-распределение ( распределение Снедекора).

Этот закон также находит важные применения при статистических исследованиях. По F-распределению распределено отношение статистических дисперсий сравниваемых величин.

Плотность вероятности этой случайной величины вычисляется по формуле:

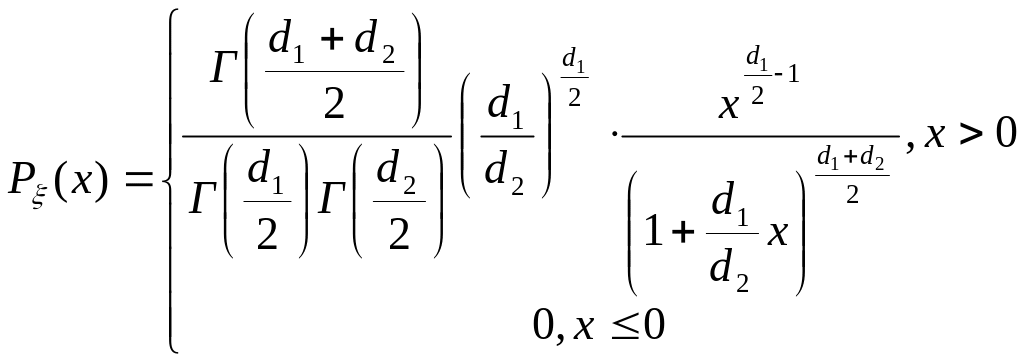
, где  - гамма-функция.

22. Распределение Стьюдента.

Этот закон также находит важные применения при статистических исследованиях(проверках). По закону распределения Стьюдента распределено отношение статистического математического ожидания к статистическому среднеквадратическому отклонению.

Плотность вероятности этой случайной величины вычисляется по формуле:

23. Логарифмическое ( логнормальное ) распределение.

Случайная величина имеет логарифмическое нормальное распределение с параметрами a и , если случайная величина ln x имеет нормальное распределение с параметрами a >и .

Функция плотности вероятностей логнормального распределения имеет вид:

24. Распределение Парето.

Применяется при анализе дохода и других экономических индексов.

Плотность вероятностей для случайной величины, распределенной по Парето, имеет вид

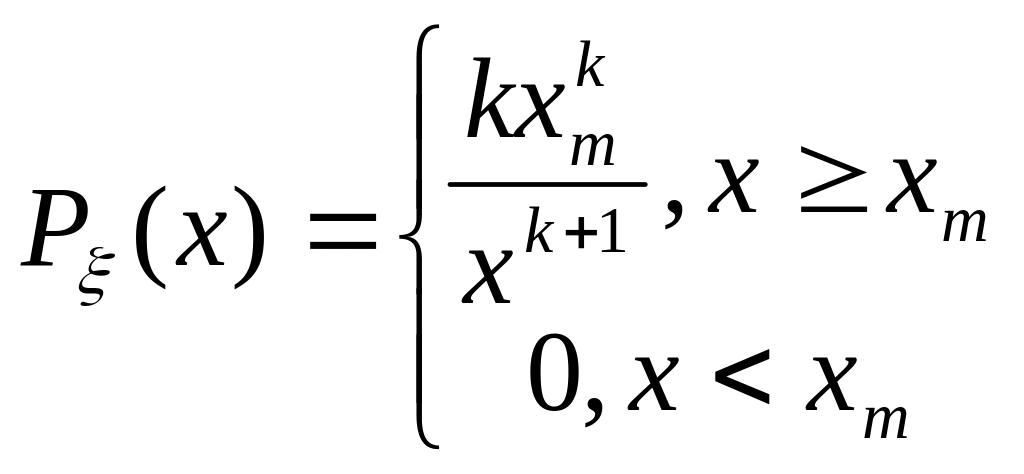
25. Z-распределение Фишера.

Плотность вероятностей для случайной величины имеет вид:

26. Распределение Вейбулла – Гнеденко.

Широко используется при оценках надежности и риска.

Случайная величина имеет распределение Вейбулла с параметрами и k , если ее функция распределения:

27. Полиномиальное распределение (мультиномиальное распределение).

Совместное распределение вероятностей случайных величин

принимающих целые неотрицательные значения

удовлетворяющие условиям

с вероятностями

где , 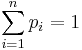; является многомерным дискретным распределением случайного вектора такого, что : (по существу это распределение является (k − 1)-мерным, так как в пространстве оно вырождено); естественным (с точки зрения современной теории вероятностей)