
Розділ 3. Побудова геометричної інтерпретації моделі множинної лінійної регресії
На окремому аркуші запишемо модель множинної лінійної регресії в аналітичному вигляді (рис. 15) та побудуємо графічну інтерпретацію моделі – площину.

Рис. 15. Запис моделі множинної лінійної регресії та початок підготовки даних для побудови її геометричної інтерпретації
Крім
того, для множинної регресії із двома
незалежними змінними можна побудувати
геометричну інтерпретацію моделі. Для
цього використаємо можливість побудови
тримірних графіків у MS
Excel.
Перш за все створимо таблицю розрахункових
вихідних даних для побудови площини за
моделлю множинної лінійної регресії в
основі якої лежать розрахункові значення
![]() (верхній ряд зазначеної таблиці) та
(крайній лівий стовпчик зазначеної
таблиці). Визначати значення даних рядів
доцільно за наступним алгоритмом:
(верхній ряд зазначеної таблиці) та
(крайній лівий стовпчик зазначеної
таблиці). Визначати значення даних рядів
доцільно за наступним алгоритмом:
Вибрати кількість розрахункових точок, наприклад 12;
За допомогою статистичних функцій МИН та МАКС внести найменше
 та найбільше
та найбільше
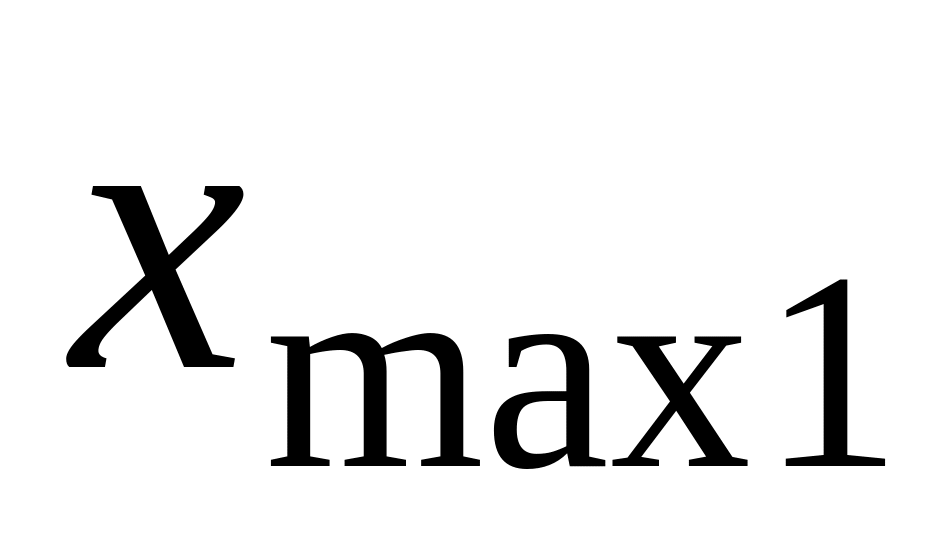 значення із вибірки даних
в крайню ліву та крайню праву комірки,
відповідно, верхнього ряду таблиці
(рис.
15).
Аналогічним чином внести найменше
значення із вибірки даних
в крайню ліву та крайню праву комірки,
відповідно, верхнього ряду таблиці
(рис.
15).
Аналогічним чином внести найменше
 та найбільше
та найбільше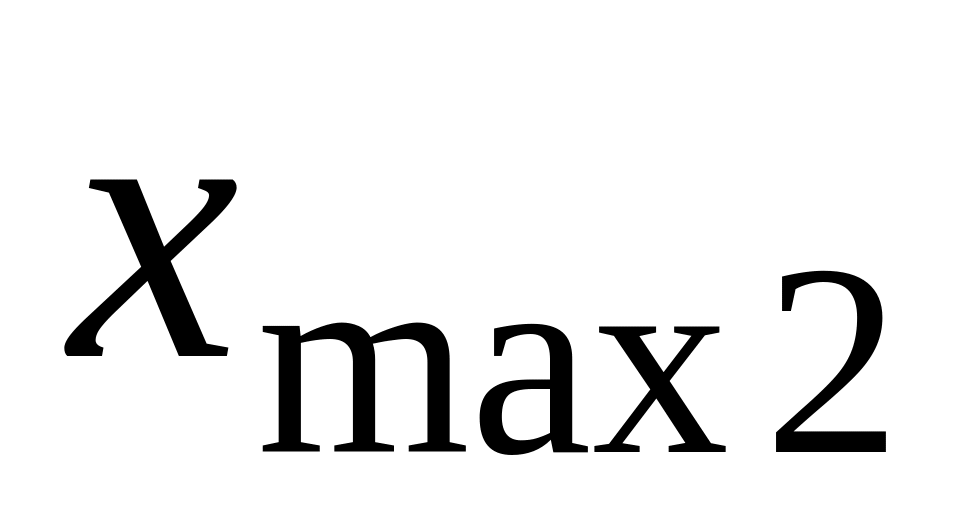 значення вибірки статистичних даних
(рис.
1) до
верхньої та нижньої комірки, відповідно,
крайнього лівого стовпчика (рис.
15).
значення вибірки статистичних даних
(рис.
1) до
верхньої та нижньої комірки, відповідно,
крайнього лівого стовпчика (рис.
15).Проміжні значення верхнього рядку розрахуємо за формулою:
![]() ,
(19)
,
(19)
де
![]() – номер незалежної змінної моделі
та
;
– номер незалежної змінної моделі
та
;
![]() – номер
розрахункового значення.
– номер
розрахункового значення.
Реалізація даних розрахунків в MS Excel показана на рис. 16.
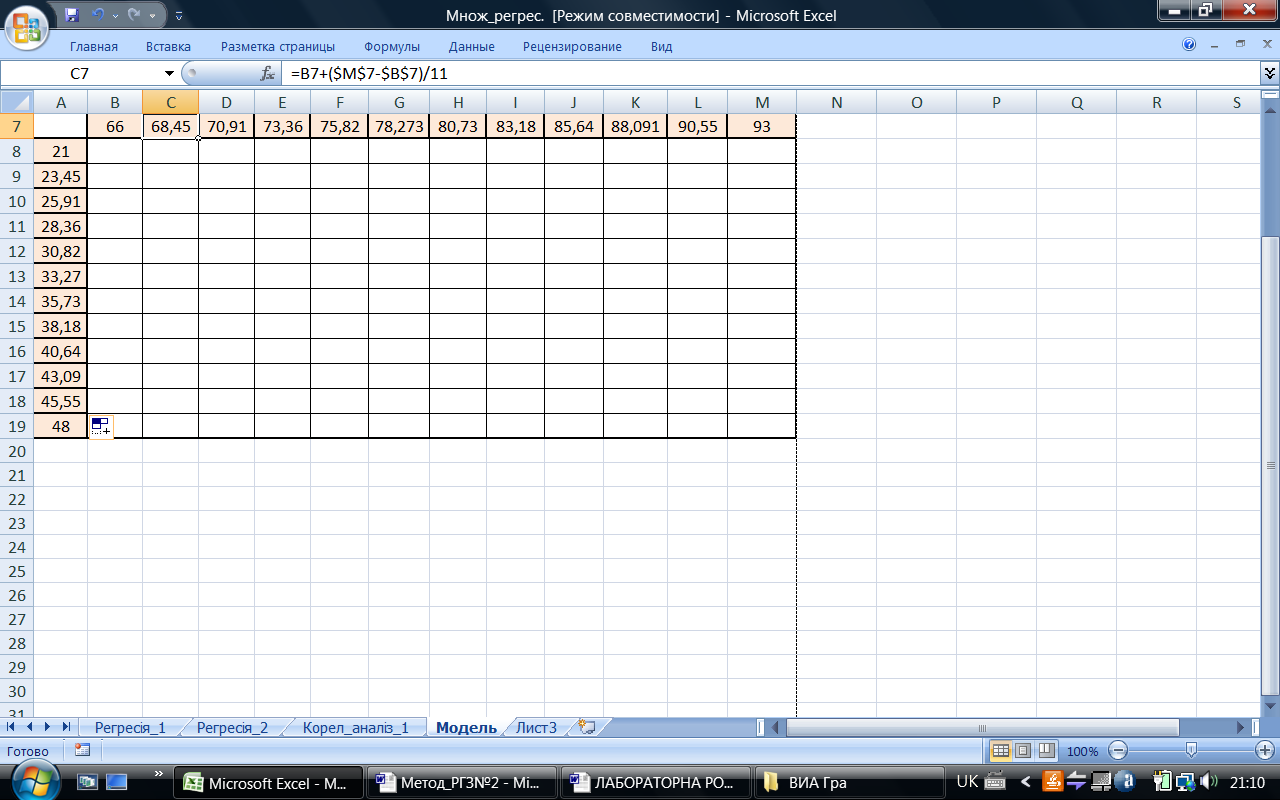
Рис. 16. Реалізація розрахунків за формулою (19) в MS Excel
Наступним етапом буде введення формули моделі множинної лінійної регресії в основний діапазон комірок таблиці (рис. 17). Параметри регресії доцільно вводити шляхом посилання на відповідні комірки звіту по результатам регресійного аналізу, причому ці посилання повинні мати абсолютну адресацію. Посилання на елементи розрахункового вектору мають мати абсолютну адресацію по рядку та відносну по стовпчику, а посилання на елементи розрахункового вектору відносну адресацію по рядку та абсолюту по стовпчику. Після заповнення першої комірки протягнемо її для всього діапазону комірок таблиці (рис. 17).
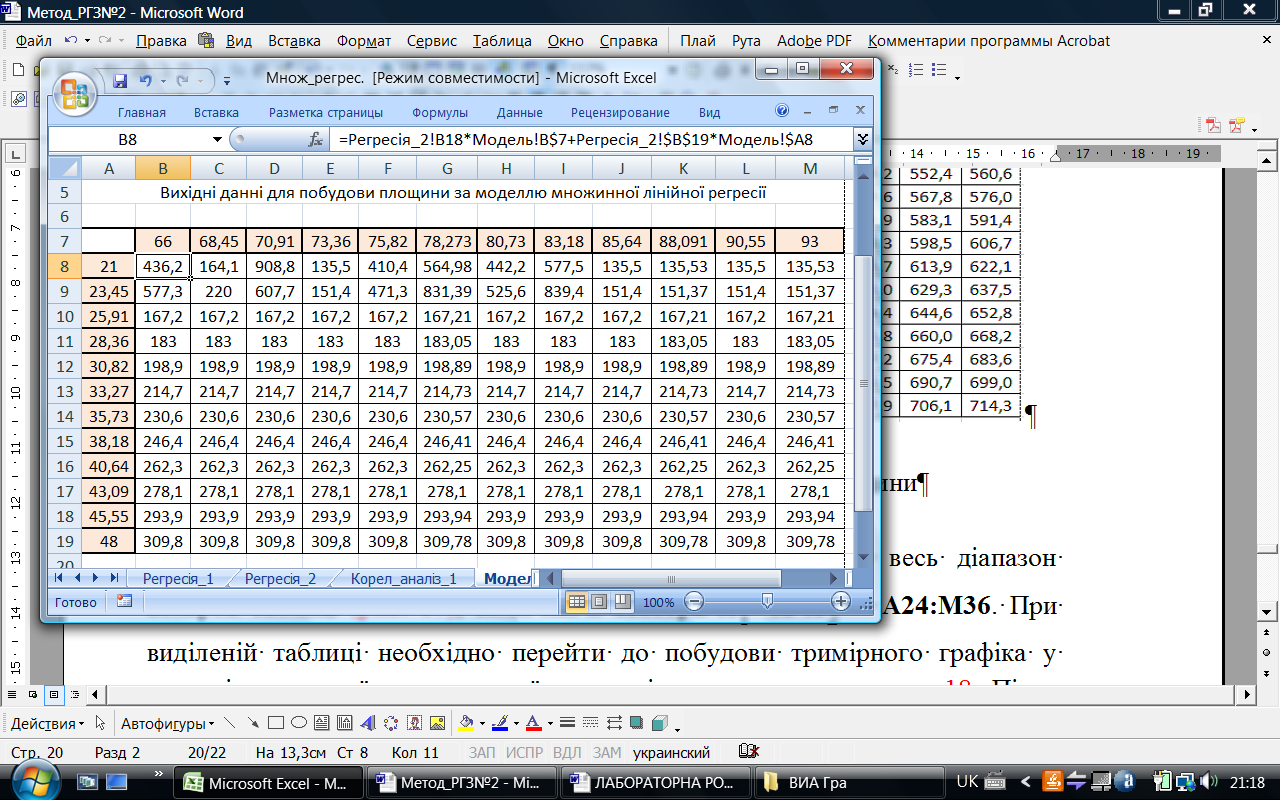
Рис. 17. Розрахункова таблиця для побудови площини
Для побудови тримірного графіку моделі виділимо весь діапазон комірок таблиці (рис. 17). При виділеній таблиці необхідно перейти до побудови тримірного графіка у вигляді так званої «проволочної поверхні», як показано на рис. 18. Після натискання значка «Проволочна поверхня» MS Excel побудує графік площини (рис. 19). Даний графік можна перемістити у будь-яке місце аркуша Excel та оформити шляхом подвійного натискання лівою кнопкою миші на полі графіка і переходу до закладки «Конструктор». Шляхом натискання правою кнопкою миші на полі графіку можна викликати додаткове меню та перейти до закладки «Поворот об’ємної авто фігури». Після даного переходу можна встановити потрібні параметри, що характеризують розташування графіку поверхні. У результаті проведеної роботи отримаємо графічну інтерпретацію нашої моделі множинної лінійної регресії із двома незалежними змінними – площину (рис. 19).
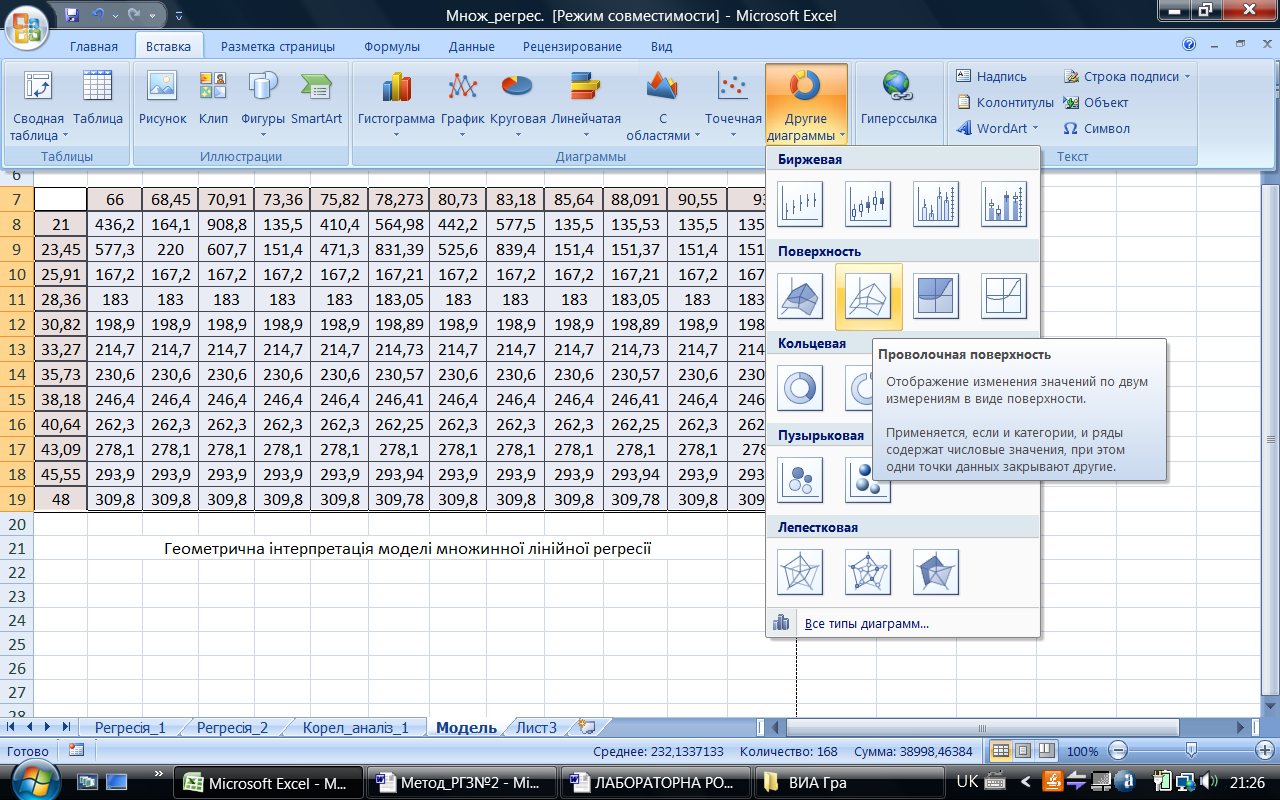
Рис. 18. Побудова графіку тримірної поверхні у MS Excel 2007
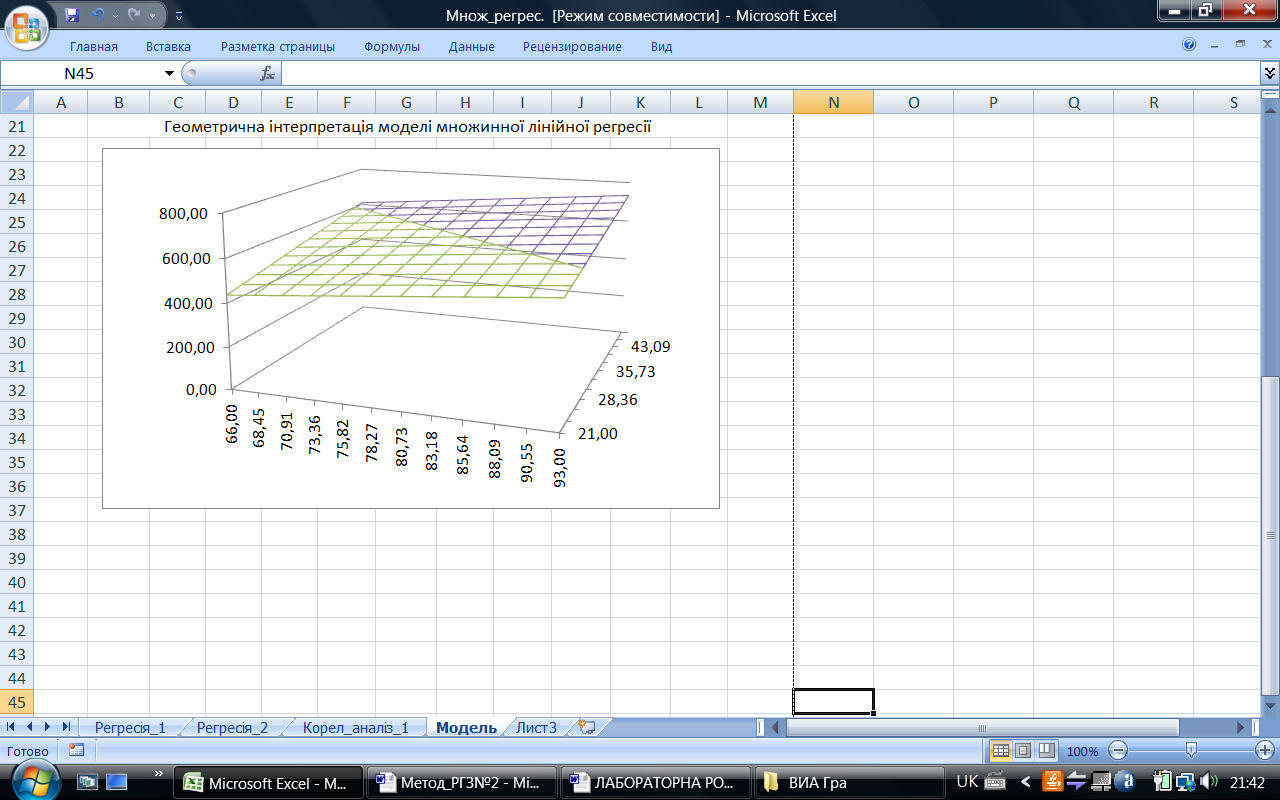
Рис. 19. Геометрична інтерпретація моделі множинної лінійної регресії
Розділ 4. Прогнозування на основі моделі множинної лінійної регресії
Як було
сказано в умовах задачі, після побудови
та дослідження якості моделі, необхідно
спрогнозувати об’єми продажів при
витратах на рекламу
![]() тис. грн. та витратах на розширення
дилерської мережі
тис. грн. та витратах на розширення
дилерської мережі
![]() тис. грн. Точковий прогноз отримаємо
підставивши ці данні в рівняння регресії
(рис
20):
тис. грн. Точковий прогноз отримаємо
підставивши ці данні в рівняння регресії
(рис
20):
![]() (20)
(20)
![]() тис грн.
тис грн.
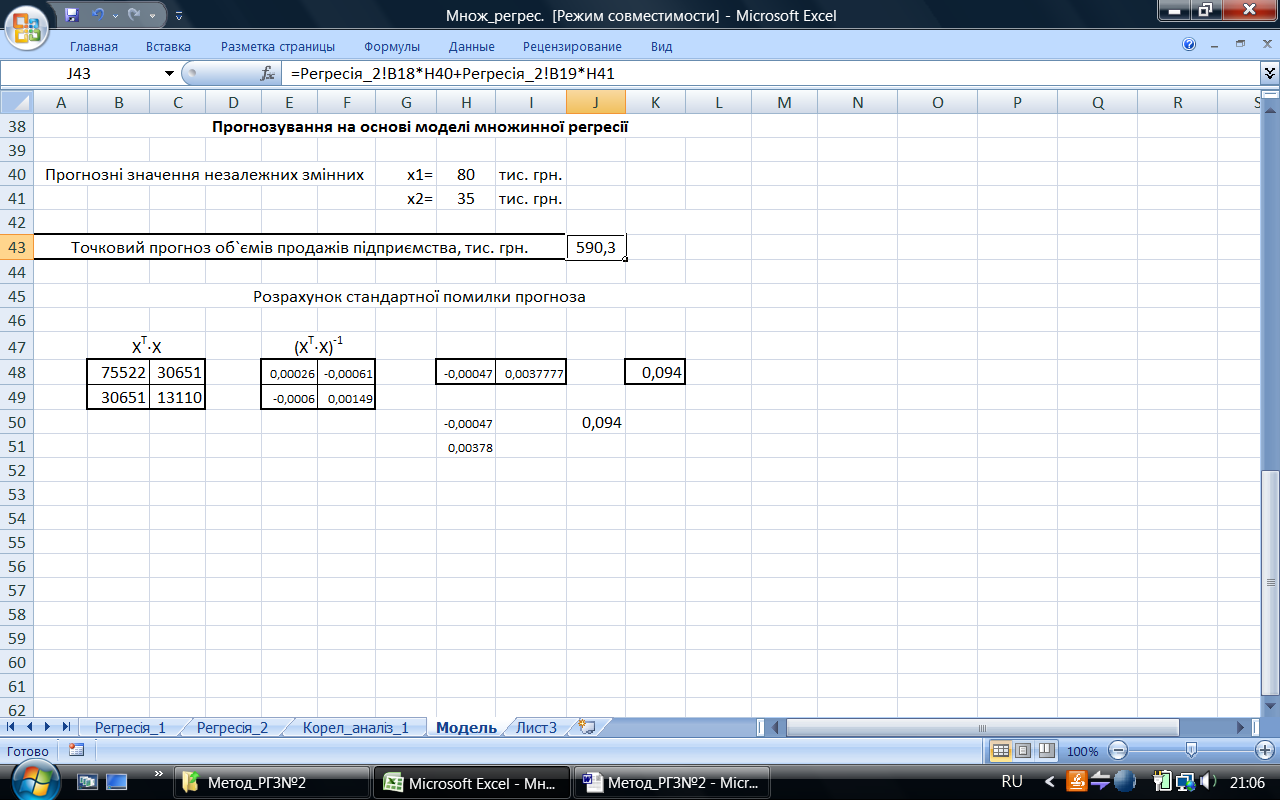
Рис. 20. Результати побудови точкового прогноза
Список використаної літератури
Кремер Н.Ш., Прутко Б.А. Эконометрика: учебник для вузов / Под ред. проф. Н.Ш. Кремера.–М.:ЮНИТИ-ДАНА,2007.–311с.
Эконометрика: Учебник / Под. ред. И.И. Елисеевой. – М.: Финансы и статистика, 2004. – 344 с.
Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс: Учеб. – 6-е изд., перераб. и доп. – М.: Дело, 2004. – 576 с.
Довідка MS Excel.
© Скворчевський О.Є., 2010
