2. Генерация окружностей. Алгоритм Брезенхема.

Существует несколько очень простых, но не эффективных способов преоб­разования окружностей в растровую форму. Например, рассмотрим для про­стоты окружность с центром в начале координат. Ее уравнение записыва­ется как x² + y² = R². Решая это урав­нение относительно y, получим

y = ±

Чтобы изобразить четвертую часть окружности будем изменять x с еди­ничным шагом от 0 до R и на каждом шаге вычислять y. Вторым простым методом растровой развертки окружности является использование вычисле­ний x и y по формулам x = R cos α, y = R sin α, при пошаговом изменении угла α от 0⁰ до 90⁰.

Для упрощения алгоритма растровой развёртки стандартной окружности можно вос­пользоваться её симметрией относительно координатных осей и прямых y = ± x в случае, когда центр окружности не совпадает с началом ко­ординат, эти прямые необходимо сдвинуть параллельно так, чтобы они прошли через центр окружности. Тем са­мым дос­таточно построить растро­вое представление для 1/8 части окружности, а все оставшиеся точки полу­чить симметрией (рис. 2.5).

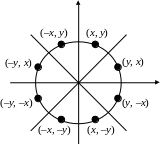
Рис. 2.1 Восьмисторонняя симметрия

Рассмотрим участок окружности из второго октанта x Є [0, R/ ]. Далее опишем алго­ритм Брезенхейма для этого участка окружности.

На каждом шаге алгоритм выбирает точку P_i (x_i, y_i), которая является бли­жайшей к ис­тинной окружности. Идея алгоритма заключается в выборе ближайшей точки при по­мощи управляющих переменных, значения которых можно вычислить в пошаговом ре­жиме с использованием небольшого числа сложений, вычитаний и сдвигов.

Рассмотрим небольшой участок сетки пикселов, а также возможные спо­собы (от A до E) прохождения истинной окружности через сетку (Рис. 2.6).

Предположим, что точка P_i-1 была выбрана как ближайшая к окружности при x = x_i-1. Теперь найдем, какая из точек S_i или T_i расположена ближе к ок­ружности при x = x_i-1 + 1.

Рис. 2.2 Варианты прохождения окружности через рас­тровую сетку

Заметим, что ошибка при выборе точки P_i (x_i, y_i) была равна

D(P_i) = (x_i²+ y_i²) – R².

Запишем выражение для ошибок, получаемых при выборе точки S_i или T_i.

D(S_i) = [(x_i-1+ 1)² + (y_i-1)²] – R²

D(T_i) = [(x_i-1+ 1)² + (y_i-1 – 1)²] – R²

Если | D(S_i) | ≥ | D(T_i) |, то T_i ближе к реальной окружности, иначе выбира­ется S_i.

Введем d_i = | D(S_i) | – | D(T_i) |

T_i будет выбираться при d_i ≥ 0, в противном случае будет устанавливаться S_i.

Опуская алгебраические преобразования, запишем d_i и d_i+1 для разных ва­риантов вы­бора точки S_i или T_i.

D₁ = 3 – 2 R

Если выбирается S_i (когда d_i < 0), то d_i+1 = d_i + 4 x_i-1 + 6

Если выбирается T_i (когда d_i ≥ 0), то d_i+1 = d_i + 4 (x_i-1 – y_i-1) + 10

3. Методы устранения ступенчатости. Причини возникновения искажения изображения. Устранение ступенчатости полутонами.

Выше было отмечено, что растровая генерация отрезков имеет следующие недостатки:  неточное расположение начала и конца,  ступенчатый вид отрезка,  яркость зависит от наклона и длины.

Ясно, что первый недостаток не может быть устранен программным путем. Неравномерность яркости обычно не слишком заметна и может быть скомпенсирована очевидным образом, требующим, в общем случае, вещественной арифметики, но в связи с реально небольшим количеством различимых уровней яркости достаточно обойтись целочисленным приближением, причем очень грубым.

Наиболее заметно ухудшает качество изображения ступенчатость. Имеется следующие способы борьбы со ступенчатостью :  увеличение пространственного разрешения за счет усовершенствования аппаратуры,  трактовка пиксела не как точки, а как площадки конечного размера, яркость которой зависит от размера площади пиксела, занятой изображением отрезка,  "размывание" резкой границы, за счет частичной подсветки пикселов, примыкающих к формируемому отрезку. Понятно, что при этом ухудшается пространственное разрешение изображения. В этом эвристическом методе интенсивность пикселя на ребре устанавливается пропорционально площади части пикселя находящегося внутри многоугольника.